Колебательное звено.
Звено называют колебательным, если связь между входной x(t) и выходной z(t) переменными определяется дифференциальным уравнением вида
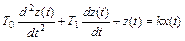 ,
,
причем корни характеристического уравнения, отвечающего этому дифференциальному уравнению
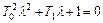 ,
,
должны быть комплексно сопряженными, т.е. должно выполнятся условие 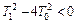 . Если это неравенство имеет противоположный знак, то корни будут вещественными и вместо колебательного звена получится последовательное соединение двух инерционных звеньев.
. Если это неравенство имеет противоположный знак, то корни будут вещественными и вместо колебательного звена получится последовательное соединение двух инерционных звеньев.
Часто дифференциальное уравнение колебательного звена записывают в ином виде, введя степень затухания (степень успокоения) ξ 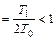 (при ξ >1 получается два инерционных звена)
(при ξ >1 получается два инерционных звена)
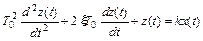 .
.
В операторной форме это уравнение может быть записано в виде
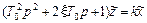 ,
,
и значит, передаточная функция звена будет такова
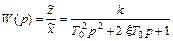 (11)
(11)
В качестве примера колебательно звена можно привести пассивный RLC – контур (рис.36).
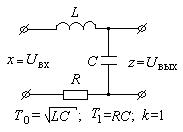
Рис.36. Пример колебательного звена.
Интересен бывает частный случай колебательного звена, когда степень затухания ξ = 0, такое звено называют консервативным. Его передаточная функция получается при ξ = 0 из (11)
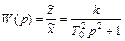 (12)
(12)
Переходная характеристика колебательного звена определяется выражением
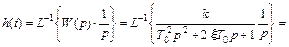
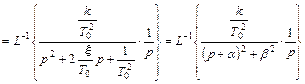
Представление выражения 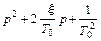 в виде
в виде 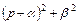 понадобилось потому, что в справочниках по операционному исчислению дается следующие стандартные выражения для обратного преобразования Лапласа
понадобилось потому, что в справочниках по операционному исчислению дается следующие стандартные выражения для обратного преобразования Лапласа
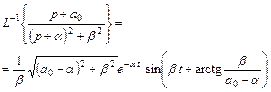 (13)
(13)
Получить введенные неизвестные коэффициенты α и β через заданные ξ и Т0 можно из выражения
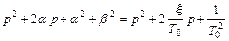 ,
,
приравняв коэффициенты при одинаковых степенях p
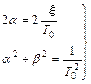 .
.
Отсюда
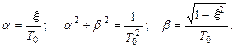 (14)
(14)
Разложим выражение в фигурных скобках для h(t) на простейшие дроби
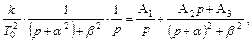
где А1, А2, А3 – неопределенные пока коэффициенты, подлежащие определению.
Приведем к общему знаменателю правую часть этого выражения, и поскольку знаменатели слева и справа окажутся одинаковыми, приравняем числители и приведем подобные.
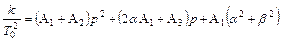 .
.
Затем, приравняв коэффициенты при одинаковых степенях переменной р, получим
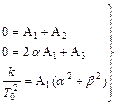 . (15)
. (15)
Из третьего равенства (15) и (14) следует, что
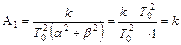
Тогда из остальных равенств (15) найдем
А2 = – А1= – k
А3 = – 2αА1= – 2αk .
Отсюда, с учетом найденных значений для А1, А2, А3, получим, имея в виду (13), 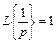 и (14)
и (14)
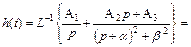
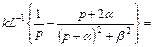
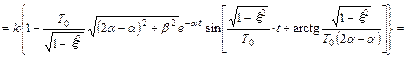
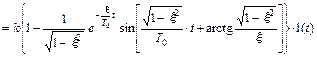 (16)
(16)
Эта переходная характеристика звена изображена на рис. 37.
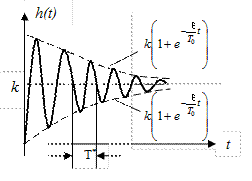
Рис. 37. Переходная характеристика колебательного звена.
Прямо из рисунка можно определить параметр k (коэффициент усиления звена) и Т* – период колебаний процесса
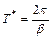 .
.
На этом же рисунке нанесены пунктиром экспоненты затухания колебаний 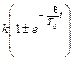 . В соответствии с этими экспонентами изменяется (здесь уменьшается) с течением времени амплитуда колебаний переходного процесса.
. В соответствии с этими экспонентами изменяется (здесь уменьшается) с течением времени амплитуда колебаний переходного процесса.
Для консервативного звена (ξ =0) экспоненты превращаются в горизонтальные линии и, следовательно, затухания колебаний не происходит (рис.38). это, впрочем, видно и из (16), если положить там ξ =0
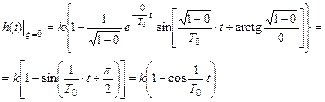
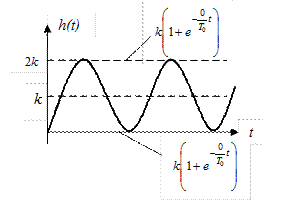
Рис. 38. Переходная характеристика
консервативного звена.
Весовая функция колебательного звена находится из выражения
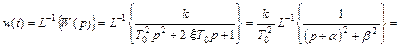
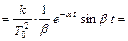
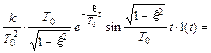
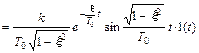 (17)
(17)
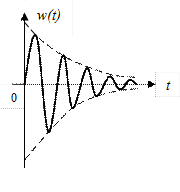
Рис. 39. Весовая функция колебательного звена.
Для случая ξ = 0, т.е консервативного звена, весовая функция найдется из выражения (17)
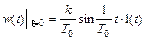
Эта характеристика изображена на рис. 40.
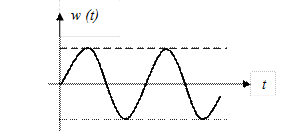
Рис. 40. Весовая функция консервативного звена.
Для исследования колебательного звена в частотной области найдем частотную передаточную функцию w(j  ) заменой в (11) р→ j
) заменой в (11) р→ j 
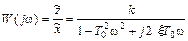 .
.
Отсюда легко получается амплитудная частотная A(  ) и фазовая частотная φ(
) и фазовая частотная φ(  ) характеристики звена.
) характеристики звена.
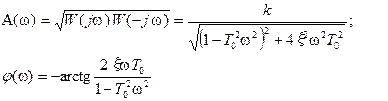 (18)
(18)
(19)
Из (18) видно, что АЧХ A(  ) существенно зависит от степени затухания ξ. Для консервативного звена (ξ = 0) при
) существенно зависит от степени затухания ξ. Для консервативного звена (ξ = 0) при 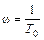 с-1
с-1 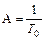 обращается в бесконечность (рис.41).
обращается в бесконечность (рис.41).
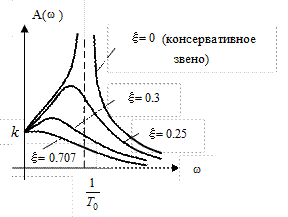
Рис. 41. АЧХ Колебательного звена.
В отношении зависимостей осей частоты ФЧХ φ(  ) следует сказать следующее. Известно, что главное значение
) следует сказать следующее. Известно, что главное значение
y = arctg(x) для положительных x изменяется от 0 до 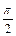 . Остальные значения y получаются из главного путем прибавления к нему величины + kπ, где k =1,2, ...
. Остальные значения y получаются из главного путем прибавления к нему величины + kπ, где k =1,2, ...
Полученное в (19) значение φ 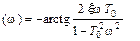 дает главное значение арктангенса от 0 до –
дает главное значение арктангенса от 0 до – 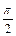 в диапазоне частот
в диапазоне частот 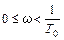 с-1 (при
с-1 (при 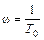 с-1 знаменатель φ(
с-1 знаменатель φ(  ) обращается в ноль, а само значение φ
) обращается в ноль, а само значение φ 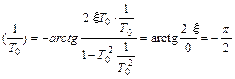 ). Для определения φ(
). Для определения φ(  ) для частот, больших
) для частот, больших 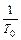 с-1 , надо, следовательно к главному значению добавлять + kπ (в нашем случае возьмем k = 1 и знак “минус”, т.к. речь идет о возрастании аргумента функции φ(
с-1 , надо, следовательно к главному значению добавлять + kπ (в нашем случае возьмем k = 1 и знак “минус”, т.к. речь идет о возрастании аргумента функции φ(  ) в отрицательную сторону). Итак, математическое выражение, характеризующие ФЧХ φ(
) в отрицательную сторону). Итак, математическое выражение, характеризующие ФЧХ φ(  ), будет разным для различных областей частот
), будет разным для различных областей частот
φ 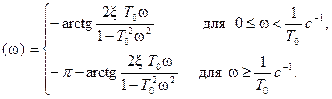 (20)
(20)
Из (20) видно, что на поведении φ(  ) сильно сказывается параметр ξ. Для консервативного звена (ξ = 0) для диапазона частот
) сильно сказывается параметр ξ. Для консервативного звена (ξ = 0) для диапазона частот 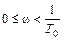 с-1 φ(
с-1 φ(  ) = 0, а для диапазона
) = 0, а для диапазона 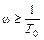 с-1 φ(
с-1 φ(  ) = – π. На рис. 42 изображены φ(
) = – π. На рис. 42 изображены φ(  ) для разных значений ξ.
) для разных значений ξ.
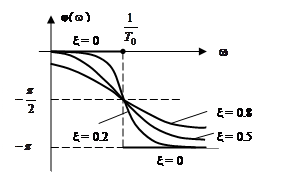
Рис. 42. ФЧХ колебательного звена.
АФХ W(j  ) колебательного звена можно построить, используя уже полученные значения A(
) колебательного звена можно построить, используя уже полученные значения A(  ) и φ(
) и φ(  ). Отметим три характерные точки рассматриваемой АФХ.
). Отметим три характерные точки рассматриваемой АФХ.
Из (18) легко получить, что А(0) = k, 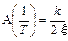 , А(∞) = 0. Аналогично из (20) получим φ(0) = 0, φ
, А(∞) = 0. Аналогично из (20) получим φ(0) = 0, φ 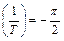 и φ(∞) = – π. Тогда качественно по этим трем точкам построим АФХ звена (рис.43)
и φ(∞) = – π. Тогда качественно по этим трем точкам построим АФХ звена (рис.43)
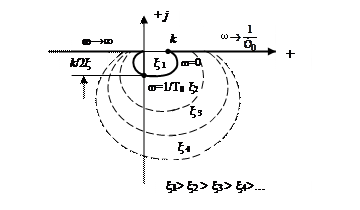
Рис. 43. АФХ колебательного звена.
Хотя A(  ) и φ(
) и φ(  )существенно зависят от степени затухания ξ, из (18) можно усмотреть, что для
)существенно зависят от степени затухания ξ, из (18) можно усмотреть, что для  = 0 и
= 0 и  = ∞ A(∞) не зависят от ξ, а (20) удостоверяет, что φ(
= ∞ A(∞) не зависят от ξ, а (20) удостоверяет, что φ(  ) не зависит от ξ при
) не зависит от ξ при  = 0,
= 0, 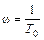 с-1 и при
с-1 и при  = ∞. Для остальных значений частоты A(
= ∞. Для остальных значений частоты A(  ) и φ(
) и φ(  ) зависят от ξ, в частности,
) зависят от ξ, в частности, 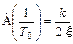 . Это означает, что с уменьшением ξ значение
. Это означает, что с уменьшением ξ значение 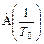 увеличивается, а сама АФХ с уменьшением ξ “разбухает”. Рассматривая предельный переход, можно сказать, что при ξ = 0 на частотах
увеличивается, а сама АФХ с уменьшением ξ “разбухает”. Рассматривая предельный переход, можно сказать, что при ξ = 0 на частотах 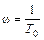 с-1 происходит разрыв АФХ и низкочастотная ее часть (т.е.
с-1 происходит разрыв АФХ и низкочастотная ее часть (т.е. 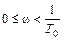 ) будет проходить по положительной част и оси абсцисс, начиная с точки k в право, а высокочастотная (
) будет проходить по положительной част и оси абсцисс, начиная с точки k в право, а высокочастотная ( 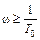 ) – по отрицательной полуоси абсцисс из – ∞ до 0. Это же можно усмотреть и из рис. III. 30 для ξ = 0: для
) – по отрицательной полуоси абсцисс из – ∞ до 0. Это же можно усмотреть и из рис. III. 30 для ξ = 0: для 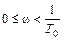 φ(
φ(  ) = 0, а для
) = 0, а для 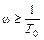 φ(
φ(  ) = – π.
) = – π.
Выражение для точной ЛАЧХ базируется на основе соотношения
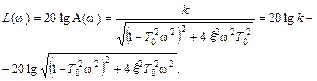 (21)
(21)
Из выражения (21)для передаточной функции видно, что звено имеет одну постоянную времени Т0 и, значит, одну сопрягающую частоту 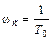 с-1 и два частотных участка.
с-1 и два частотных участка.
I участок
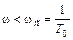 ,
, 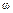 T0<1.
T0<1.
Для получения первой асимптоты надо в выражение для точной ЛАЧХ подставить это условие 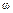 T0<1, справедливое для первого участка.
T0<1, справедливое для первого участка.
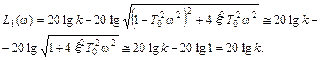
Итак, первая асимптота есть прямая, проходящая параллельно оси абсцисс на расстоянии 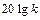 от нее.
от нее.
II участок.
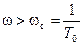 ,
, 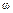 T0>1.
T0>1.
Тогда выражение для второй асимптоты будет
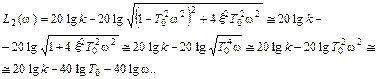
Таким образом, вторая асимптота есть прямая линия с наклоном – 40 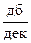 , проходящая через конечную точку первой асимптоты.
, проходящая через конечную точку первой асимптоты.
На рис. 44 представлена асимптотическая ЛАЧХ. Выше для инерционного звена указывалось, что максимальное отличие асимптотической ЛАЧХ от точной не превышает 3,03 дб. Для колебательного звена, из-за зависимости его характеристик от параметра ξ, эти отличия могут быть много больше, так что имеются специальные таблицы, которые предназначены внести поправки для различных ξ в асимптотические ЛАЧХ, чтобы приблизить их к точным. На рис.44 точные значения ЛАЧХ (в том числе и для ξ =0) нанесены пунктиром. Видно, что максимальные отличия точной ЛАЧХ от асимптотической находятся вблизи частоты 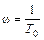 с-1, вдали же от этой частоты различия практически исчезают.
с-1, вдали же от этой частоты различия практически исчезают.
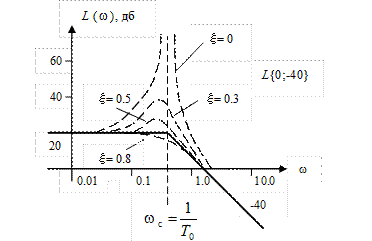

Рис. 44. ЛАЧХ колебательного звена.
Упругое звено.
Упругое звено описывается дифференциальным уравнением вида
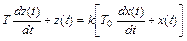 .
.
Примерами упругого звена (см. рис.45) могут служить пассивные четырехполюсники вида
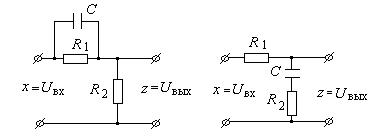
Рис. 45. Примеры упругого звена.
Если к вышеприведенному дифференциальному уравнению упругого звена применить преобразование Лапласа, то для нулевых начальных условий получим
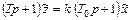 ,
,
и следовательно, передаточная функция звена будет
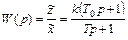 (22)
(22)
Характеристики упругого звена существенно зависят от параметра 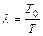 . При λ > 1, т.е. при Т0 > T звено называется упругим дифференцирующим, в противном случае, при λ < 1 – упругим интегрирующим.
. При λ > 1, т.е. при Т0 > T звено называется упругим дифференцирующим, в противном случае, при λ < 1 – упругим интегрирующим.
Переходная характеристика упругого звена находится обычным путем.
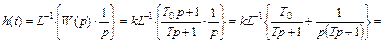

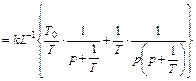 .
.
Поскольку
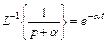 ,
,
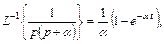
то получим для h(t)
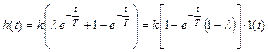 .
.
Для построения этой зависимости найдем значение h(t) при t = 0 и t→ ∞:
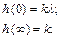
Легко понять, что для упругого дифференцирующего звена (λ > 1) h(0) > h( ∞), а для упругого интегрирующего звена (λ < 1) h(0) < h( ∞). В соответствии с этим зависимости h(t) для λ > 1 и λ < 1 примет вид, изображенный на рис. 46 а, в.
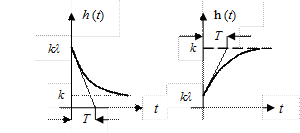
а) λ >1 в) λ < 1
Рис. 46. Переходная характеристика упругого звена.
Весовая функция звена может быть определена из соотношения
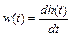 .
.
В нашем случае
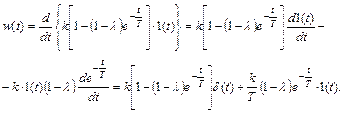
Первое слагаемое этого выражения равно нулю для всех t ≠ 0 (ибо δ(t) = 0 при t ≠ 0), а при t = 0
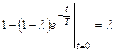 ,
,
поэтому
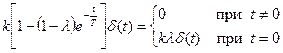
Окончательно 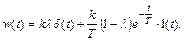
Видно, что весовая функция (рис. 47) состоит из двух составляющих – первая 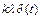 - это δ – функция площадью kλ, проходящая по оси ординат, и вторая
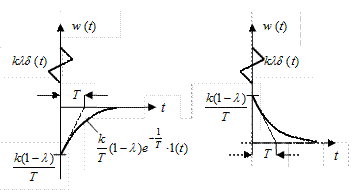
- это δ – функция площадью kλ, проходящая по оси ординат, и вторая 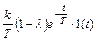 существует для всех t ≥ 0. Кроме того, из последнего выражении можно усмотреть, что весовая функция w(t) упругого звена зависит от параметра λ. Следовательно, графики w(t) дифференцирующего (λ >1) и интегрирующего (λ <1) упругих звеньев (рис. 47 а, б) будут иметь различный вид
существует для всех t ≥ 0. Кроме того, из последнего выражении можно усмотреть, что весовая функция w(t) упругого звена зависит от параметра λ. Следовательно, графики w(t) дифференцирующего (λ >1) и интегрирующего (λ <1) упругих звеньев (рис. 47 а, б) будут иметь различный вид
а) λ >1 в) λ < 1
Рис. 47. Весовая функция упругого звена.
Частотная передаточная функция звена, исходя из (22), имеет вид
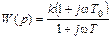 .
.
Следовательно, амплитудная частотная A(  ) и фазовая частотная φ(
) и фазовая частотная φ(  ) характеристики могут быть представлены следующим образом
) характеристики могут быть представлены следующим образом
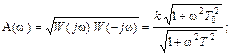
φ 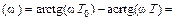 φ1(
φ1(  ) – φ2(
) – φ2(  )
)
Отсюда видно, что A(  ) и φ(
) и φ(  ) зависят от постоянных времени Т0 и Т и, значит, от параметра
) зависят от постоянных времени Т0 и Т и, значит, от параметра 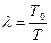 . При λ >1, т.е. Т0>T или
. При λ >1, т.е. Т0>T или 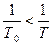 , зависимости A(
, зависимости A(  ), φ(
), φ(  ) и w(
) и w(  ) представлены на рис. III. 36, а при λ < 1, т.е Т0 < T или
) представлены на рис. III. 36, а при λ < 1, т.е Т0 < T или 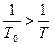 - на рис. 48. при построении A(
- на рис. 48. при построении A(  ) при
) при  → ∞ следует иметь в виду, что
→ ∞ следует иметь в виду, что
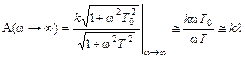 .
.

а) в) с)
Рис. 48. A(  ), φ(
), φ(  ) и w(
) и w(  ) упругого дифференцирующего звена (λ > 1).
) упругого дифференцирующего звена (λ > 1).

а) в) с)
Рис. 49. A(  ), φ(
), φ(  ) и w(
) и w(  ) упругого интегрирующего звена (λ < 1).
) упругого интегрирующего звена (λ < 1).
Выражение для точной ЛАЧХ определяется следующим образом:
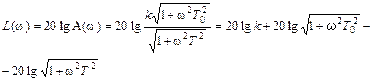
Видно, что передаточная функция звена имеет два постоянных времени Т0 и Т, значит, асимптотическая ЛАЧХ содержит две сопрягающие частоты 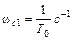 и
и 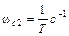 , и три частотных участка.
, и три частотных участка.
Рассмотрим сначала случай λ >1, т.е. 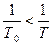 (рис. 50)
(рис. 50)
I участок
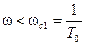 ,
,  T0<1.
T0<1.
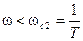 ,
,  T<1.
T<1.
Тогда выражение для первой асимптоты с учетом этих неравенств примет вид
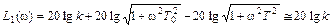 .
.
Это уравнение прямой, проходящей на I участке параллельно оси абсцисс на расстоянии от нее 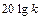 (если, допустим, примем, что k = 0.1, то L1(
(если, допустим, примем, что k = 0.1, то L1(  ) = – 20 дб).
) = – 20 дб).
II участок
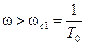 ,
,  T0>1.
T0>1.
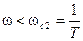 ,
,  T<1.
T<1.
С учетом этих неравенств уравнение для второй асимптоты получится из выражения для точной ЛАЧХ в следующем виде
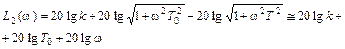
Получим уравнение прямой, проходящей через конец первой асимптоты с наклоном +20 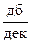 .
.
III участок
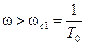 ,
,  T0>1.
T0>1.
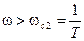 ,
,  T>1.
T>1.
Для этого участка уравнение асимптоты примет вид
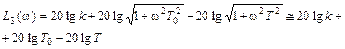
Это выражение характеризует горизонтальную прямую, проходящую через конец второй асимптоты.
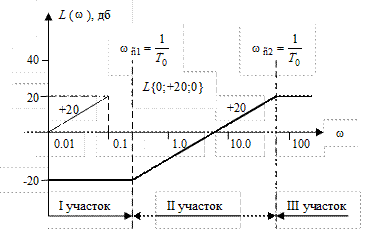
Рис. 50. ЛАЧХ упругого дифференцирующего звена (λ >1).
Построение ЛАЧХ можно сильно упростить, если воспользоваться нижеследующей методикой.
Первая асимптота ЛАЧХ заканчивается на сопрягающейся частоте 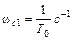 , которой соответствует постоянная времени
, которой соответствует постоянная времени 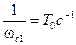 . Из выражения для передаточной функции (22) видно, что эта постоянная времени расположена в скобке
. Из выражения для передаточной функции (22) видно, что эта постоянная времени расположена в скобке 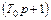 , находящейся в числителе. Известно мнемоническое правило, что если скобка
, находящейся в числителе. Известно мнемоническое правило, что если скобка 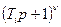 находится в числителе, то ЛАЧХ на частоте
находится в числителе, то ЛАЧХ на частоте 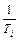 претерпевает излом на +
претерпевает излом на + 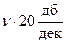 , а если в знаменателе, то
, а если в знаменателе, то 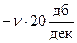 .
.
В нашем случае 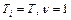 , и, следовательно, ЛАЧХ “ломается” на +20
, и, следовательно, ЛАЧХ “ломается” на +20 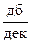 . Поэтому, раз наклон первой асимптоты был ноль, а на частоте
. Поэтому, раз наклон первой асимптоты был ноль, а на частоте 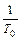 ЛАЧХ изменила его на +20
ЛАЧХ изменила его на +20 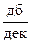 , то наклон ЛАЧХ на II участке будет 0+20
, то наклон ЛАЧХ на II участке будет 0+20 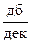 = 20
= 20 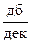 . Сопрягающей частоте
. Сопрягающей частоте 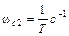 соответствует постоянная времени Т. с, которая, как видно из (III. 1.22) расположена в скобке, находящейся в знаменателе. Значит, на частоте
соответствует постоянная времени Т. с, которая, как видно из (III. 1.22) расположена в скобке, находящейся в знаменателе. Значит, на частоте  c2 ЛАЧХ претерпевает излом на -20
c2 ЛАЧХ претерпевает излом на -20 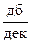 и наклон ЛАЧХ на III участке будет -20
и наклон ЛАЧХ на III участке будет -20 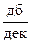 +20
+20 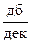 = 0.
= 0.
Рассмотрим теперь случай λ <1, т.е 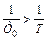 (рис. 51).
(рис. 51).
I участок.
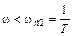 ,
,  T<1.
T<1.
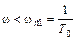 ,
,  T0 <1.
T0 <1.
Выражение для первой асимптоты выглядит следующим образом.
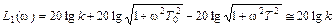 .
.
Итак, первая асимптота – прямая линия, параллельная оси частот и отстоящая от нее на расстоянии 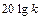 ( например при k = 1000
( например при k = 1000 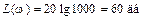 ). Первая асимптота заканчивается частотой
). Первая асимптота заканчивается частотой 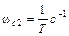 , которой соответствует постоянная времени Т, расположена в скобке, находящейся в знаменателе передаточной функции звена. Значит, ЛАЧХ на частоте
, которой соответствует постоянная времени Т, расположена в скобке, находящейся в знаменателе передаточной функции звена. Значит, ЛАЧХ на частоте 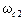 претерпевает излом на -20
претерпевает излом на -20 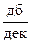 , а вторая асимптота будет проходить с наклоном 0 –20
, а вторая асимптота будет проходить с наклоном 0 –20 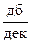 = – 20
= – 20 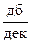 до сопрягающей частоты
до сопрягающей частоты 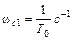 . Этой частоте соответствует постоянная времени Т0, расположенная в скобке числителя (22). Следовательно, ЛАЧХ на частоте
. Этой частоте соответствует постоянная времени Т0, расположенная в скобке числителя (22). Следовательно, ЛАЧХ на частоте 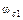 “изломается” на +20
“изломается” на +20 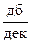 и суммарный наклон ЛАЧХ на III участке будет -20
и суммарный наклон ЛАЧХ на III участке будет -20 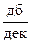 + 20
+ 20 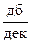 = 0.
= 0.
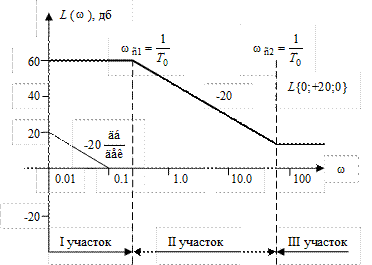
Рис. 51. ЛАЧХ упругого интегрирующего звена (λ < 1).
Из сказанного понятно, что на всех участках, кроме первого, определить наклон асимптот ЛАЧХ указанным способом не представляет сложности. Позже в III.2 будет показано, как также просто строить и первую асимптоту.
Дата добавления: 2017-01-13; просмотров: 5592;
