Колебательное звено

Звено называется колебательным, если его уравнение движения имеет вид

T²x⁽²⁾ + 2Txx⁽¹⁾ + x = kg (5.20)

или может быть приведено к такому виду, причем величина x должна быть меньше единицы. Колебательное звено характеризуется тремя параметрами, к которым относятся:

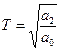- постоянная времени;

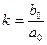- передаточный коэффициент;

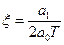- относительный коэффициент затухания.

Здесь a₁, a₂, a₀, b₀ – коэффициенты уравнения, записанного в нестандартной форме:

a₂x⁽²⁾ + a₁x⁽¹⁾ + a₀x = b₀g.

В дальнейшем будем пользоваться уравнением (5.20).

Передаточная функция колебательного звена определяется выражением

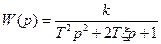. (5.21)

Заменяя р на jw , получим частотную передаточную функцию

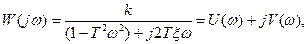(6.21)

где

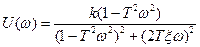- вещественная частотная характеристика;

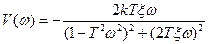- мнимая частотная характеристика.

Модуль функции (5.22)

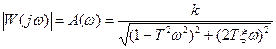(5.23)

является амплитудной частотной характеристикой, а ее аргумент

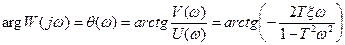(5.24)

является фазовой частотной характеристикой колебательного звена. Графики характеристик A(w) и q(w) (рис.5.7,а,б) можно построить, меняя частоту w от 0 до ¥ : при w=0 A(w)=k, q(w)=0; при 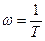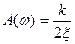, q(w)=-90°; при w®¥ A(w)®0, q(w)®180°.

На вид характеристик A(w) и q(w) оказывает влияние величина x. Чем меньше x, тем больше пик амплитудной частотной характеристики A(w) и тем круче изгиб фазовой частотной характеристики q(w) на частотах близких к 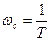. Если x=0, то на частоте 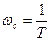пик характеристики A(w) уходит в бесконечность.

Амплитудно-фазовая характеристика (АФХ) колебательного звена представляет собой кривую, показанную на рис.5.7,в.

Эта кривая, как и АФХ апериодического звена, начинается в точке k (при w=0) на вещественной оси. С увеличением частоты модуль вектора W(jw) изменяется; при 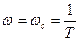АФХ пересекает мнимую ось в точке 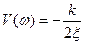; при w®¥ характеристика подходит к началу координат, касаясь отрицательной части вещественной оси.

На рис.5.7,в показан вид двух АФХ колебательного звена (при x=x₁ и x=x₂, x₂>x₁).

Из графиков, приведенных на рис.5.7, следует, что при малых значениях коэффициента относительного затухания x и частотах w, близких к 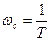, усиление входного сигнала по амплитуде во много раз превосходит величину коэффициента преобразования k звена. Это явление используется, например, в радиотехнике при усилении слабых сигналов.

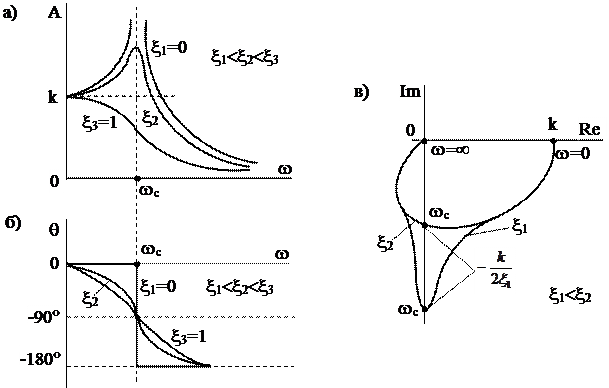Рис.5.7. Частотные характеристики колебательного звена:

а – амплитудная; б – фазовая; в – амплитудно-фазовая

Из графиков фазовой частотной характеристики q(w) (рис.5.7,б) видно, что колебательное звено, как и апериодическое, создает отрицательный сдвиг по фазе между выходным и входным гармоническими сигналами, т.е. вносит отставание по фазе. С уменьшением величины x фазовый сдвиг в полосе частот 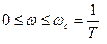уменьшается при уменьшении w, а в полосе частот 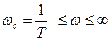увеличивается при увеличении w, достигая величины -180°.

Логарифмические амплитудная L(w) и фазовая j(w) частотные характеристики колебательного звена определяются выражениями:

L(w) = 20 lg A(w) ;

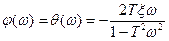. (5.25)

На основании выражения (5.23) при k=1 можем написать

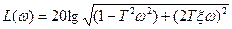. (5.26)

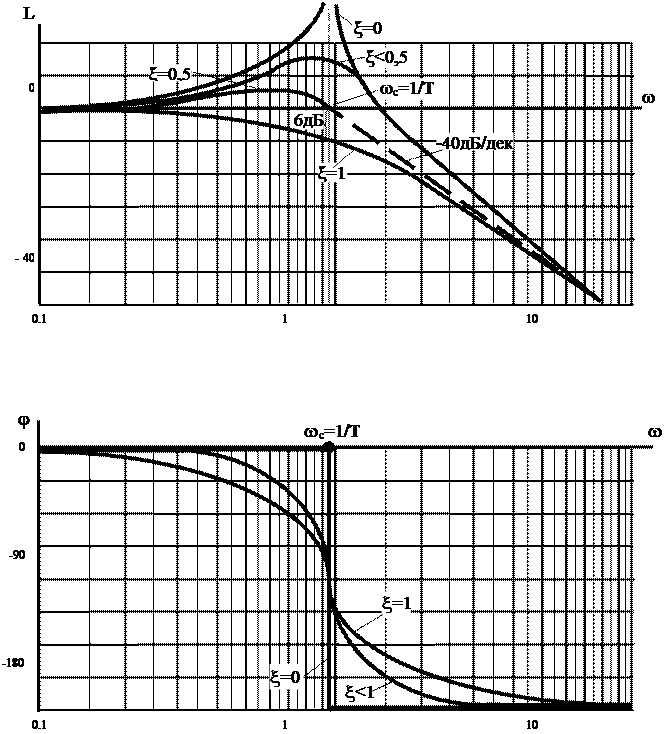
Выражение (5.26) позволяет построить точную логарифмическую амплитудную частотную характеристику звена при k=1. Для различных значений x получается серия кривых, некоторые из которых изображены на рис.5.8,а.

При k¹1 ЛАЧХ смещается на величину 20 lg k , при k>1 – вверх и при k<1 – вниз.

Пользуясь выражением (5.25), можно построить логарифмические фазовые частотные характеристики (ЛФЧХ), вид которых также зависит от величины x (рис.5.8,б).

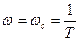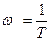Анализ формул (5.25) и (5.26) показывает, что с уменьшением x увеличивается пик ЛАЧХ и крутизна ЛФЧХ около точки . При L(w)=-20lg2x , причем при x=0,5 L(w)=0, а при x=0 L(w)®¥, т.е. ЛАЧХ терпит разрыв. Характеристика j(w) изменяется от 0° при w=0 до -180° при w®¥.

Для облегчения построения ЛАЧХ колебательного звена пользуются более простыми выражениями по сравнению с выражением (5.26), которые позволяют построить приближенную (асимптотическую) характеристику. Нетрудно заметить, что при wT<<1, т.е. при частотах 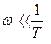в формуле (5.26) можно пренебречь по сравнению с единицей величинами T²w² и (2Txw)².

Рис.5.8. Логарифмические частотные характеристики колебательных звеньев

Тогда:

L(w) » -20 lg 1 = 0 при k = 1

и

L(w) » 20 lg k при k ¹ 1.

Эти выражения определяют асимптоту ЛАЧХ в области достаточно низких частот, совпадающую с осью частот при k=1 или параллельную ей при k ¹ 1. При значениях wT >> 1, т.е. в области достаточно высоких частот 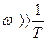, можно пренебречь единицей и величиной (2Txw)² по сравнению с (T²w²)². Тогда выражение

L(w) » -20 lg T²w² = -40 lg Tw

определяет вторую асимптоту приближенной ЛАЧХ, наклоненную к оси частот. Наклон данной асимптоты равен –40 дБ\дек.

Таким образом, точная кривая ЛАЧХ колебательного звена может быть заменена приближенной, которая состоит из двух отрезков указанных выше асимптот, сопрягающихся в точке 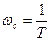. Асимптотическая ЛАЧХ показана на рис.5.8 пунктирной линией. Как видно из рисунка, она отличаются от точных характеристик. Величина ошибки зависит от величины коэффициента x. При x<0,5 ошибки от замены точной ЛАЧХ отрезками двух асимптот будут очень большими, поэтому в этих случаях пользуются специальными таблицами поправок или кривыми поправок в децибелах.

Логарифмические характеристики L(w) и j(w) могут быть просто и быстро построены с помощью шаблонов, профиль которых выполнен для различных x по формулам (5.25) и (5.26).

Примером колебательного звена является электрическая цепь, состоящая их дросселя с индуктивностью L , активного сопротивления R , включающего сопротивления обмотки дросселя, и конденсатора с емкостью С, соединенных последовательно (рис.5.9). Входной величиной является напряжение U_вх , приложенное ко всей цепи, выходной величиной – напряжение U_вых , снимаемое с конденсатора. Передаточная функция цепи

,

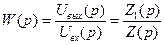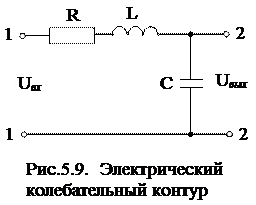
где Z(p) и Z₁(p) – символические (операторные) сопротивления, определяемые выражениями:

и .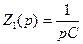

Отсюда получаем уравнение цепи в операторной форме:

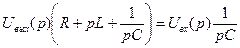
или

.

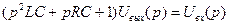Переходя от изображений выходной и входной величин к оригиналам, получим следующее уравнение:

.

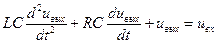Обозначив T²=LC , 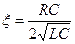, k=1, получим уравнение в стандартной форме (5.20). При x<1 рассмотренная цепь является колебательным контуром, который широко применяется в технике.