Апериодическое (инерционное) звено

Апериодическим звено называется звено, уравнение динамики которого имеет вид

a₁x⁽¹⁾ + a₀x = b₀g , (5.8)

или может быть приведено к такому виду.

В стандартной форме уравнение (5.8) можно переписать так:

Tx⁽¹⁾ + x = kg , (5.9)

где 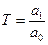- постоянная времени звена, характеризующая его динамические свойства;

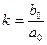- коэффициент преобразования, определяющий статические свойства звена.

Передаточная функцияW(p) может быть получена путем применения преобразования Лапласа к уравнению движения звена. Уравнение устойчивого апериодического звена (6.8) в операторной форме при нулевых начальных условиях имеет вид:

TpX(p) + X(p) = kG(p) . (5.10)

Отсюда по определению

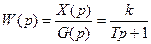. (5.11)

Полагая p=jw, получим выражение частотной передаточной функции W(jw). Так, из выражения (5.11) при p=jw находим, что

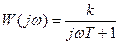. (5.12)

Освобождаясь от иррациональности в знаменателе, преобразуем формулу (5.12) к виду

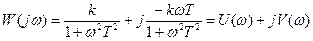, (5.13)

где 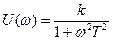- вещественная частотная характеристика звена;

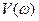
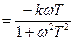- мнимая частотная характеристика звена.

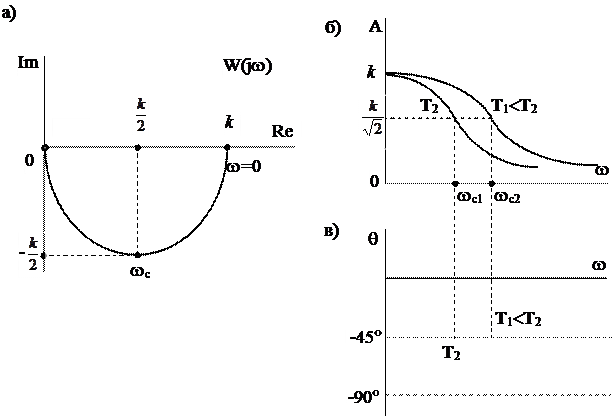Пользуясь выражением (5.13) и изменяя частоту w от 0 до ¥, построим амплитудно-фазовую характеристику. При w=0 V(w)=0, U(w)=k; при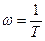 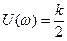, 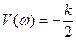; при w®¥ U(w)=V(w)=0. Нетрудно заметить, что амплитудно-фазовая характеристика апериодического звена (рис.5.5,а) представляет собой полуокружность с диаметром, равным k , и с центром на вещественной положительной полуоси на расстоянии 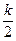от начала координат.

w=¥

Рис.5.5. Частотные характеристики апериодического звена:

а – амплитудно-фазовая характеристика; б, в – амплитудная и фазовая частотные характеристики

Амплитудно-частотная характеристика описывается выражением

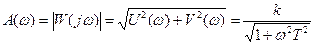. (5.14)

Ее график (рис.5.5,б) может быть построен при изменении w от 0 до ¥ : при w=0 A(w)=k; при 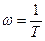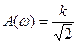, при w®¥ A(w)=0. Из графика A(w) следует, что апериодическое звено сильно ослабляет колебания высоких частот и, следовательно, является фильтром низких частот.

Аргумент функции W(jw), равный

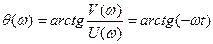, (5.15)

определяет фазовую частотную характеристику звена. График этой характеристики (рис.5.5,в) может быть построен при изменении w от 0 до ¥. Так, при w=0 q(w)=0°; при 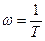q(w)=-45°, наконец, при w®¥ q(w)®-90°. Из выражения (5.15) и графика, приведенного на рис.5.5,в, видно, что при w, близких к нулю, звено не дает сдвига по фазе выходной величины по отношению ко входной величине. При всех значениях частоты w>0 апериодическое звено создает отрицательный сдвиг по фазе (об этом свидетельствует знак «минус» в выражении q(w)), т.е. вносит запаздывание.

Логарифмические частотные характеристики звена определяются выражениями:

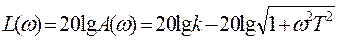; (5.16)

j(w) = arctg (-wT) = q(w) . (5.17)

В частности, при k=1

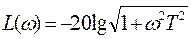. (5.18)

Рассмотрим построение характеристик L(w) и j(w) для этого частного случая. Следует заметить, что выражение (5.18) можно заменить двумя более простыми выражениями, справедливыми для областей достаточно низких частот 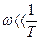и достаточно высоких частот 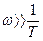. Действительно, если 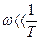, т.е. wT<<1, то величина w²T² мала, и ею можно пренебречь, по сравнению с единицей. Тогда

L(w) » -20 lg1 = 0.

При 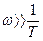или, иначе, при wT>>1 справедливо выражение

L(w) » -20 lg wT . (5.19)

Это уравнение прямой, пересекающей ось частот в точке 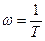, где L(w)=0 дБ. Из приведенных рассуждений следует, что график L(w) может быть приближенно представлен ломаной, состоящей из отрезков двух прямых (асимптот): L(w)=0, совпадающей с осью частот в диапазоне частот 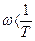, и L(w)=-20 lgwT, наклоненной к оси частот, в диапазоне частот 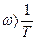, которые сопрягаются в точке 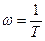. Данная частота, поэтому называется сопрягающей частотой и обозначается w_с.

Определим наклон второй асимптоты к оси абсцисс, вычислив приращение ее ординаты на некотором заданном интервале частот. В теории автоматического управления за такой интервал принимают декаду, т.е. интервал частот, граничные значения которого отличаются в 10 раз. Для рассматриваемого звена при w₁=w_i L(w₁)=-20 lg (w_iT), w₂ = 10w_i и L(w₂)= -20lg(10w_iT) = -20lg(w_iT) - 20lg10.

Отсюда

DL = L(w₂) – L(w₁) = -20 lg10 = -20 дБ.

Следовательно, асимптота (1.68) имеет наклон – 20 децибел на декаду (сокращенно –20дБ\дек.).

Асимптотическая характеристика показана на рис.5.6,а сплошной линией. Здесь же приведена точная логарифмическая амплитудно-частотная характеристика (ЛАЧХ), показанная пунктирной линией, которая строится по формуле (5.18) и несколько отличается от приближенной характеристики. Наибольшая ошибка, имеющая место при частоте 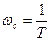, равна:

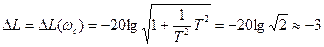дБ.

При k¹1 графики приближенных ЛАЧХ строятся по формулам:

L(w) = 20 lg k при ;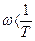

L(w) = 20 lg k – 20 lg wT при ,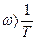

А графики точной ЛАЧХ – по формуле (5.19).

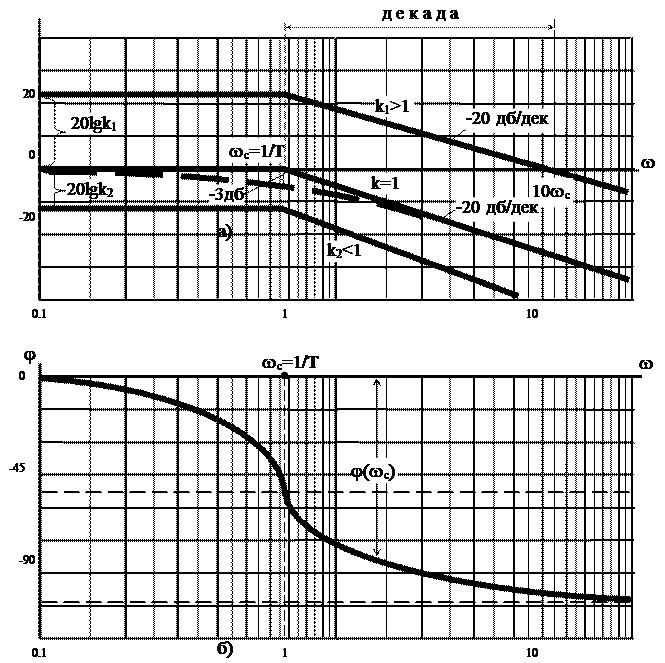
Рис.5.6. Логарифмические частотные характеристики апериодического звена: а – амплитудно-частотная; б – фазовая характеристика

Указанные графики отличаются от вышерассмотренных смещением относительно оси частот на величину 20 lg k вверх при k>1 или вниз при k<1 (рис.5.6,а). График логарифмической фазовой частотной характеристики (ЛФЧХ) приведен на рис.5.6,б.