Классификация типовых динамических звеньев.

Любая САУ состоит из взаимосвязанных друг с другом элементов, различающихся по своему назначению, принципу действия и конструкции. Но классификация элементов САУ по этим признакам не имеет существенного значения при исследовании самих элементов и САУ, так как, имея различия по своей физической природе и конструктивному оформлению, элементы могут описываться одинаковыми дифференциальными уравнениями.

Элементы САУ, рассматриваемые с точки зрения динамических свойств, называются динамическими звеньями. Классификация элементов по виду дифференциальных уравнений позволяет типизировать элементы и ввести понятие “типовое” или элементарное звено.

Рассмотрим передаточную функцию системы

.

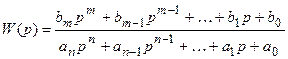Это выражение на основании информации о нулях и полюсах передаточной функции можно представить так:

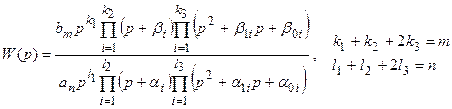(5.1)

где

составляющие 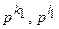- определяются нулевыми корнями соответствующих полиномов;

составляющие 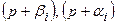- определяются вещественными корнями полиномов, многочленов передаточной функции;

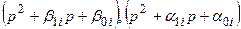- комплексные корни полиномов.

Звено, устройство, система называются динамическими, если они описываются дифференциальными уравнениями и характеризуются временными процессами.

Типовым (элементарным) динамическим звеном называется звено, которое описывается дифференциальным уравнением не выше второго порядка.

Звено, система называются минимально-фазовыми, если все нули и полюса соответствующей передаточной функции имеют отрицательные или равные нулю вещественные части ( 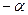, , 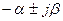, , 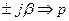, 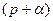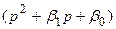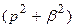). Минимально-фазовые звенья, системы имеют однозначную зависимость между амплитудными и фазовыми характеристиками, а также, как правило, минимальные значения фазовых характеристик при одних и тех же амплитудно-частотных характеристик. Это приводит к более простым методам исследования.

Звено, система называются неминимально-фазовыми, если соответствующие передаточные функции содержат хотя бы один ноль или полюс с положительной вещественной частью. В таких системах нет однозначного соответствия между амплитудными и фазовыми частотными характеристиками.

Классификация. На основании анализа передаточной функции (5.1) можно выделить следующие типовые (элементарные) динамические звенья (минимально-фазовые) по виду их передаточных функций:

1. Усилительное (пропорциональное) звено, .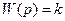

2. Интегрирующее звено, .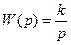

3. Дифференцирующее звено, .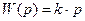

4. Апериодическое (инерционное) звено, .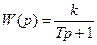

5. Форсирующее звено первого порядка, .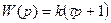

6. Колебательное звено, .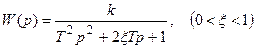

7. Форсирующее звено второго порядка, .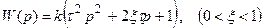

8. Консервативное звено, .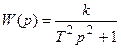

Усилительное звено

Для усилительного звена уравнение, связывающее выходную и входную координаты, имеет вид

a₀x = b₀g или x = kg , (5.2)

где 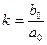- коэффициент преобразования;

x и g – установившиеся значения величин на выходе и входе звена.

Если размерности x и g одинаковы, то величину k называют коэффициентом усиления.

Усилительное звено является самым простым из типовых динамических звеньев.

Из выражения (5.2) и рис. 5.1 следует, что выходной сигнал копирует

Рис.5.1. К определению переходной функции усилительного звена

входной сигнал без всякого искажения и запаздывания. Поэтому усилительное звено называют иначе безинерционным звеном. Итак, переходная характеристика звена h(t) является ступенчатой функцией. Если входной сигнал g(t)=H 1(t), где H=const, то выходная величина будет ступенчатой функцией с «высотой ступеньки», равной kH , т.е. x=kH 1(t).

Импульсная характеристика усилительного звена

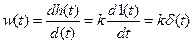(5.3)

является импульсом с площадью S=k , т.е. численно равной величине коэффициента преобразования.

Передаточная функция усилительного звена

W(p) = k , (5.4)

т.е. является постоянной величиной.

Частотная передаточная функция W(jw) = k. Отсюда следует, что вещественная и мнимая частотные характеристики звена соответственно равны U(w)=k и V(w)=0. Поэтому амплитудная и фазовая частотные характеристики определяются выражениями:

A(w) = k ; q(w) = 0 . (5.5)

Графики амплитудной и фазовой частотных характеристик звена приведены на рис. 5.2(а, б). Из графиков видно, что усилительное звено не дает сдвига по фазе, а амплитуда входного сигнала на всех частотах изменяется в k раз (усиливается в k раз при k>1).

Рис.5.2. Частотные характеристики усилительного звена

Амплитудно-фазовая характеристика звена W(jw) вырождается в точку на вещественной оси на расстоянии k от начала координат (рис.5.2,в).

Логарифмические частотные характеристики

L(w) = 20 lg A(w) = 20 lg k, (5.6)

j(w) = q(w) = 0 (5.7)

приведены на рис.5.3. Очевидно, что при k=1 характеристика L(w) совпадает с осью частот, при k>1 – лежит выше ее, а при k<1 располагается ниже оси, причем при k¹1 характеристика смещается параллельно оси частот на величину 20 lg k.

Примерами усилительных звеньев являются электронный операционный усилитель постоянного тока (рис.5.4,а), делитель напряжения (рис.5.4,б) и рычаг (рис.5.4,в).

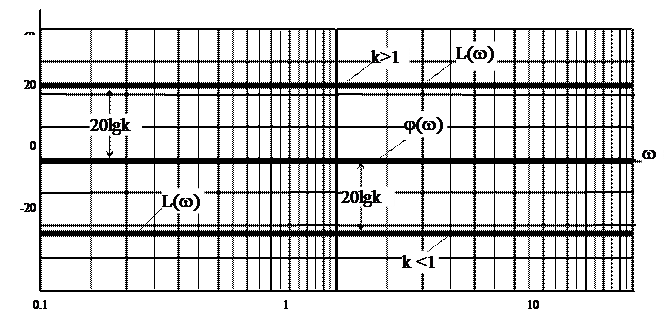
Рис.5.3. Логарифмические частотные характеристики

усилительного звена

Примерами усилительных звеньев являются электронный операционный усилитель постоянного тока (рис.5.4,а), делитель напряжения (рис.5.4,б) и рычаг (рис.5.4,в).

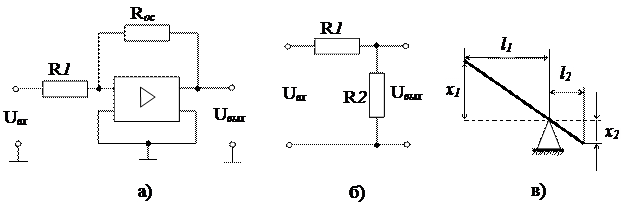
Рис.5.4. Примеры усилительных звеньев

Для операционного усилителя выходное и входное напряжения связаны соотношением U_вых=k_uU_вх , где k_u – коэффициент усиления по напряжению, определяемый выражением 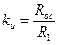. Если число каскадов усилителя нечетное, то U_вых= -kU_вх. Знак «минус» означает, что полярность выходного напряжения противоположна полярности входного напряжения. Такие усилители называются инвертирующими.

Для схемы, приведенной на рис.5.4,б, U_вых=kU_вх , где 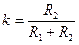- коэффициент усиления. Очевидно, для этой схемы всегда k<1.

Для рычага коэффициент усиления в зависимости от соотношения плеч l₁ и l₂ может быть больше или меньше единицы. Прикладывая силу к длинному плечу, получаем выигрыш в силе, т.е. рычаг можно рассматривать как механическое усилительное звено. Если перемещение правого конца рычага х₂ принять за выходную величину, а перемещение левого конца х₁ за входную величину, то получим выражение

x₂ = kx₁ , где .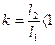

Данное выражение является уравнением усилительного звена (сравните с выражением (5.2)).