Интегрирующее звено.

Процесс в интегрирующем звене описывается уравнением вида

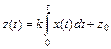. (2.10)

Продифференцировав это интегральное уравнение по времени, можно его представить в виде дифференциального уравнения

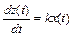. (2.11)

Такое звено называют еще астатическим или нейтральным.

Если перейти в последнем уравнении в Лапласовую область, то можно получить передаточную функцию звена

,

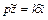отсюда

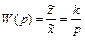. (2.12)

Примерами интегрирующих звеньев могут служить: электрическая емкость (рис.25 а); индуктивность (б); вращающийся вал (в), если за входной его сигнал считать угловую скорость вращения 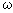, а за выходной сигнал – угол поворота вала φ; гидравлический резервуар (г); операционный усилитель в режиме интегрирования (д).

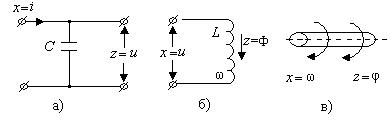
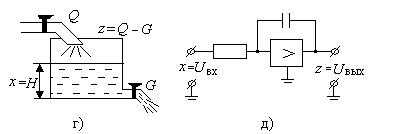
Рис.2.12. Примеры интегрирующих звеньев.

Действительно, напряжение на емкости

,

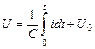магнитный поток в индуктивности

,

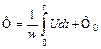угол поворота вала

φ 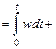φ₀,

уровень воды в гидравлическом резервуаре

,

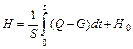напряжение на выходе операционного усилителя

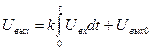
описываются интегральными уравнениями, аналогичными уравнению интегрирующего звена (26).

В этих уравнениях приняты следующие обозначения: i – ток в емкости С, u – напряжение на катушке с числом витков w, Q – приток воды в резервуар, G – слив воды из резервуара, S – поверхность резервуара.

Найдем переходную характеристику звена

.

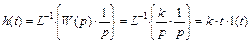Импульсная переходная (весовая) функция определяется следующим образом

.

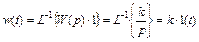На рис. 26 представлены обе эти характеристики.

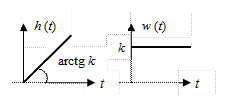
Рис. 2.13. Временные характеристики

интегрирующего звена.

По имеющейся передаточной функции звена найдем частотную передаточную функцию:

,

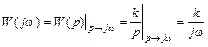а затем и АЧХ и ФЧХ

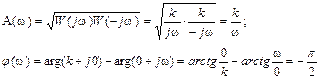
эти зависимости изображены на рис. 2.14.

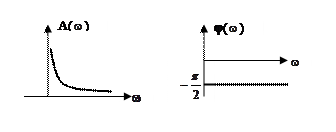
Рис. 2.14. АЧХ и ФЧХ интегрирующего звена.

АФХ интегрирующего звена (рис. 2.15) построена на основании зависимостей A(ω) и φ(ω). Подчеркнем, что для всех частот 0 ≤ ω < ∞, фазовый угол звена равен 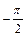, т.е. АФХ звена пройдет по отрицательной полуоси ординат.

Выражение для точной ЛАЧХ звена

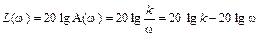
дает уравнение прямой линии с наклоном -20 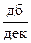, т.е. эту точную ЛАЧХ не надо заменять асимптотой.

Поскольку ЛАЧХ наклонена, то она пересекает ось абсцисс (т.е. становится равной нулю) при некоторой частоте среза ω_c

,

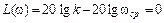отсюда

ω_cр = k

и ЛАЧХ интегрирующего звена выглядит следующим образом (рис. 2.16):

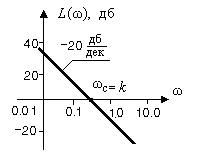
Рис. 2.16. ЛАЧХ интегрирующего звена.