Интегрирующее устройство
Предыдущие устройства аналоговой обработки сигналов имели цепи частотно-независимой ООС, т.е. b=const и не зависит от частоты. Интегрирующий и дифференцирующий усилители, в отличие от предыдущих устройств, имеют частотно-зависимые цепи ООС. Для этого в цепи ОС включает емкость, сопротивление которой зависит от частоты.
Интегрирующий усилитель строится на основе инвертирующего усилителя, заменив в цепи обратной связи R2 на С, рис. 20.7.
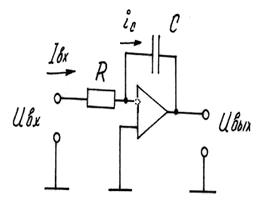
Рис. 20.7. Функциональная схема интегрирующего устройства
Вследствие второго допущения имеем
Iвх+ic=0, 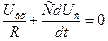
Левый вывод заземлен, поэтому выходное напряжение равно напряжению на конденсаторе.
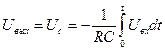 (20.5)
(20.5)
Если на вход подается постоянный скачок напряжения, то
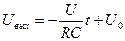 , выходное напряжение линейно возрастает со временем. Знак “-“ говорит о том, что наклон отрицательный.
, выходное напряжение линейно возрастает со временем. Знак “-“ говорит о том, что наклон отрицательный.
При подаче на вход прямоугольных импульсов можн࠾ получить пил࠾࠾бразное напряжение. Если входной сигнал представляет собой переменное напряжение по косинусоидальному закону, т.е. Uвх=Uвхcosωt, то 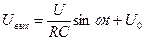 .
.
Амплитудно-частотная характеристика интегрирующего устройства в двойном логарифмическом масштабе строго должна соответствовать ФНЧ 1-го порядка со спадом, равным 6 дБ на октаву или 20 дБ на декаду.
Коэффициент усиления интегрирующего усилителя легко получить из коэффициента усиления инвертирующего усилителя, заменив R2 на Хс,
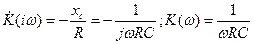 . (20.6)
. (20.6)
Из выражения (20.6) видно, что с увеличением частоты уменьшается К(ω) . Как уже было отмечено, в отличие от предыдущих устройств, b зависит от частоты 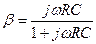 и является комплексным. На высоких частотах b=1 и фазовый сдвиг цепи ОС равен нулю, как при частотно-независимом. Точность интегрирования зависит от выбора постоянной интегрирования t=RC и от параметров ОУ. Для повышения точности желательно использовать скорректированные ОУ с малым Iвх.
и является комплексным. На высоких частотах b=1 и фазовый сдвиг цепи ОС равен нулю, как при частотно-независимом. Точность интегрирования зависит от выбора постоянной интегрирования t=RC и от параметров ОУ. Для повышения точности желательно использовать скорректированные ОУ с малым Iвх.
Дата добавления: 2016-07-09; просмотров: 1539;
