Усилительное звено.

Самым простейшим звеном является безынерционное звено, которое не только в статическом, но и динамическом режиме описывается алгебраическим уравнением.

z(t)=k·x(t) (2.1)

Предполагается, что передача сигнала от входа к выходу производится мгновенно без какой либо инерции. Поэтому такое звено называют безынерционным. Примерами таких звеньев являются механический редуктор, безинерционный операционный усилитель, делитель напряжения, рычажная передача и т.п.

После применения к алгебраическому уравнению (1) преобразования Лапласа

,

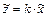получим передаточную функцию звена

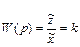. (2.2)

Рассмотрим сначала временные характеристики безынерционного звена. Как уже говорилось в п.2., переходная функция звена h(t) есть его реакция на единичный скачек 1(t),поэтому согласно п.2.

.

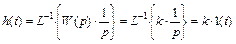В выражениях для переходных характеристик h(t) имеется сомножитель

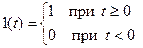
Этот сомножитель вводится для того, чтобы подчеркнуть, что h(t), является следствием приложения ко входу звена в момент времени t = 0 единичного скачка 1(t), может существовать (не быть равной нулю) только при t ≥0. Для моментов времени t < 0, когда 1(t) = 0, т.е. скачок еще не приложен, реакция на него h(t <0) равна нулю. Если на одном рис. 2.2 поместить рядом входной единичный сигнал x(t) = 1(t) звена, и выходной z(t) = h(t) = k1(t), то легко понять, что параметр k, входящий в выражение для передаточной функции и в уравнение (2.1) есть коэффициент усиления безынерционного звена.

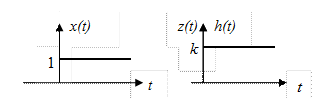
Рис. 2.2. Единичный скачок и переходная функция

безынерционного звена.

Импульсная переходная или весовая функция звена w(t) есть его реакция на единичный импульс δ(t). Поскольку 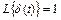, то

.

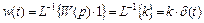Таким образом, если на вход безынерционного звена подать импульс δ(t) бесконечно малой длительности и бесконечно большой амплитуды с площадью, равной единице, то на выходе получится такой же импульс, но с площадью, равной k, т.е. .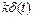

Чтобы получить частотные характеристики звена, надо в его передаточной функции провести замену 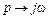. Тогда получится частотная передаточная функция безынерционного звена

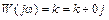, (2.3)

где k = Re (W(j ω)),

0j = Jm (W(j ω)).

Амплитуднo- частотная А(ω) (АЧХ) и фазо- частотная φ(ω) (ФЧХ) характеристики звена легко определяются из выражений:

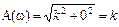
φ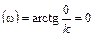

Эти зависимости приведены на рисунке 2.3.

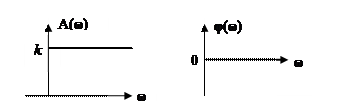
а) б)

Рис. 2.3. АЧХ и ФЧХ безынерционного звена.

Из рис. 2.3 для пункта а) видно, что безынерционное звено является некоторой идеализацией реальных звеньев. В действительности ни одно звено не в состоянии равномерно пропускать все частоты от 0 до ∞. Обычно к такому виду звена сводится одно из реальных звеньев, рассматриваемых ниже, например, инерционное или колебательное, если можно пренебречь влиянием динамических (переходных) процессов в этом звене.

Амплитудно-фазовая характеристика безынерционного звена отличается тем, что для всех ее точек, соответствующих частотам от 0 до ∞, фазовый угол φ(ω) = const = 0 и АЧХ А(ω) = const = k, т.е. АФХ звена представляет собой точку на оси абсцисс плоскости Гаусса, отстающую от начала координат на расстояние k (рис. 2.4).

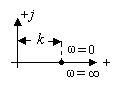
Рис. 2.4. АФХ безынерционного звена.

Для построения ЛАЧХ безынерционного звена воспользуемся зависимостью 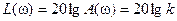. Это уравнение прямой, проходящей на расстоянии 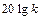от оси абсцисс параллельно ей, т.е. независимо от частоты (рис.2.5).

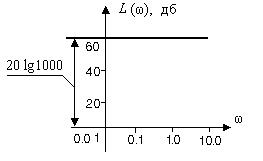
Рис. 2.5. ЛАЧХ безынерционного звена для k =1000

Инерционное звено.

Звено называется инерционным, если связь между входным х(t) и выходным z(t) сигналами звена определяется дифференциальным уравнением:

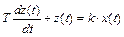. (2.4)

Смысл коэффициентов T и k будет пояснен позже. Такое звено называют также апериодическим, статистическим, одноемкостным, релаксационным.

Надо заметить, что этот тип звена наиболее часто встречается в практике автоматического управления. В качестве примеров инерционного звена можно назвать термопару, магнитный усилитель, двигатель постоянного тока с независимым возбуждением, генератор и т.д.

Если к (2.4) применить преобразование Лапласа, при нулевых начальных условиях, то получится

.

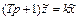Найдем отсюда передаточную функцию звена

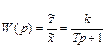. (2.5)

Переходная характеристика звена определиться из выражения

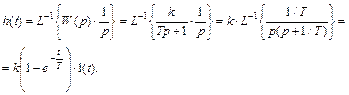(2.6)

На рисунке 2.6 представлены для сравнения сигналы х(t) = 1(t) и z(t) = h(t) инерционного звена.

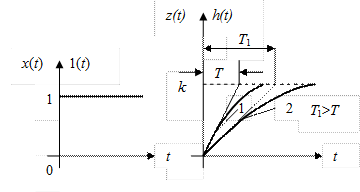
Рис. 2.6. Единичный скачок и переходная

функция инерционного звена.

Из рисунка видно, что, сравнивая установившиеся значение выходного сигнала звена k и величину входного 1(t), можно сделать вывод, что параметр k в (2) есть коэффициент усиления звена. Из этого же рис. 20. видно, что кривая 2 характеризует более замедленную, более инертную реакцию звена на единичный скачок. Для кривой 2 параметр Т₁ (смысл которого ясен из рисунка) больше параметра Т₂ для кривой 1.Значит, этот параметр может служить мерой инерционности звена. Обычно, этот коэффициент Т называют постоянной времени звена.

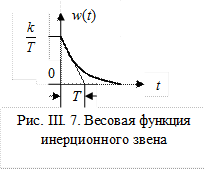
Импульсная переходная (весовая) функция звена w(t), представленная на рис. 2.7, определяется следующим образом

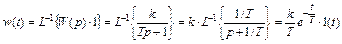. (2.7)

Получим частотную передаточную функцию звена W(jω), заменив в (2.5) р на jω

.

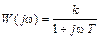Отсюда легко определяются АЧХ A(ω) и ФЧХ φ(ω)

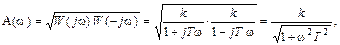
φ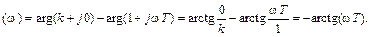

Качественный вид графиков, соответствующих выше найденным зависимостям A(ω) и φ(ω), представлен на рис. 2.8.

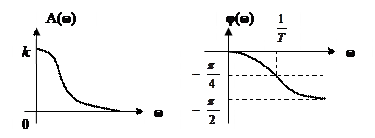
Рис.2.8. АЧХ и ФЧХ инерционного звена.

По найденным графикам A(ω) и φ(ω) на рис. 2.9 построена амплитудно-фазовая характеристика инерционного звена

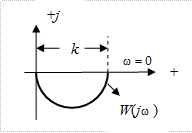
Рис. 2.9. АФХ инерционного звена.

Из выражения для АЧХ звена выводится точное соотношение для ЛАЧХ:

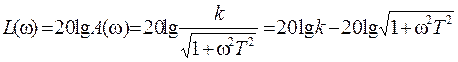. (2.8)

В выражении для L(ω) вычислять слагаемое 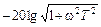для различных частот от 0 до ∞ представляет определенные неудобства. Вот если бы удалось диапазон частот 0 ≤ ω < ∞ так разбить на два (в данном конкретном случае) поддиапазона, чтобы в каждом из них кривая линия 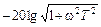была бы заменена прямой линией (асимптотой) с собственным наклоном, вычисления существенно бы упростилось.

В качестве первого участка возьмем диапазон частот, для которого 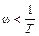или ωT<1. Тогда в выражении для асимптоты первого порядка вторым слагаемым подкоренного выражения 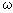²T² можно пренебречь по сравнению с первым

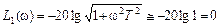
Итак, первая асимптота представляет собой прямую линию, не зависящую от частоты, и проходящую по оси частот. Наклон такой асимптоты равен 0.

На втором участке рассмотрим диапазон частот, для которого 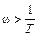или ωT >1. Тогда асимптота второго участка может быть получена, если в выражении 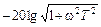пренебречь первым слагаемым подкоренного выражения по сравнению со вторым

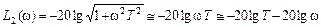. (2.9)

Поскольку при построении ЛАЧХ по оси абсцисс частоты откладываются в логарифмическом масштабе, то вторая асимптота представляет собой уравнение прямой, зависящей от частоты ω (т.е. проходящей с некоторым наклоном к оси частот). Ниже будет показано, как определять наклон таких асимптот.

Когда же сопрягаются, т.е. становятся равными эти две асимптоты L₁(ω) и L₂(ω)? Очевидно, тогда, когда первое слагаемое подкоренного выражения точной кривой 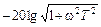становится равным второму

1= ω²T².

Отсюда частота, при которой сопрягаются обе асимптоты, или сопрягающая частота

.

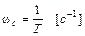Асимптоты L₁(ω) и L₂(ω) представляют собой совокупность прямых, приблизительно заменяющих точную кривую 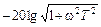(рис.23). На этом рисунке помимо асимптот L₁(ω) и L₂(ω) пунктиром показана и упомянутая точная кривая.

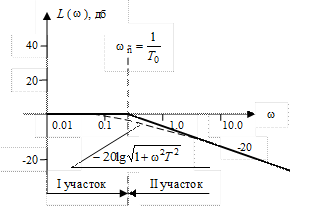
Рис. 2.10. Точная ЛАЧХ 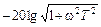и ее асимптоты.

Вернемся к выражению (2.8) для точной ЛАЧХ звена и построим асимптоты, приблизительно ее заменяющие.

Начинать построение ЛАЧХ рекомендуется с определения сопрягающих частот. Сопрягающих частот у ЛАЧХ будет столько, сколько звено (или САР) имеет постоянных времени. В случае инерционного звена из рис. 2.10 видно, что имеется лишь одна постоянная времени Т и, значит, одна сопрягающая частота

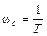
Эта сопрягающая частота делит ось частот на два участка ω < ω_c и ω > ω_c. Для более сложных звеньев или САР число постоянных времени может достигать произвольного значения m, тогда число участков будет m+1.

В случае инерционного звена рассмотрим:

I участок

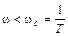или ω T<1.

Выражение для асимптоты I участка L₁(ω) получим из соотношения (4) для точной ЛАЧХ, если учтем условие (5), т.е. в подкоренном выражении члена 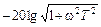пренебрежем вторым слагаемым по сравнению с первым. Тогда получится:

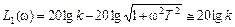
Это уравнение горизонтальной прямой (ее значение не зависит от частоты ω), проходящей при k =100 на расстоянии 20lg100=40 дб от оси абсцисс до частоты ω_c:

II участок

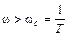или ω T >1.

Выражение для асимптоты II участка получается аналогично предыдущему случаю, только учитывать надо условие (6) и в члене 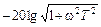следует пренебречь первым слагаемым по сравнению со вторым

.

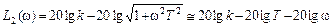Как уже говорилось выше, с учетом логарифмического масштаба по оси частот данное выражение представляет собой прямую линию, имеющий некоторый наклон к оси абсцисс. Чтобы провести эту асимптоту на графике, необходимо знать ее наклон и точку, через которую проходит данная прямая. Что касается упомянутой точки, то найти ее легко, если понять, что конец предыдущей асимптоты является началом следующей. В самом деле, если взять конец первой асимптоты, т.е. ее значение при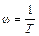

,

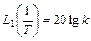и начало второй асимптоты, т.е. опять же ее значение при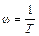

,

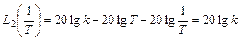то подтверждается вышеприведенное утверждение

.

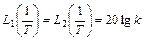Для определения наклона асимптоты к оси абсцисс найдем для частоты ω^*, относящейся ко II участку

.

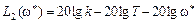Затем увеличим частоту ω^* в 10 раз (т.е. на декаду) и получим значение L₂(10 ω^*)

.

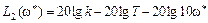Легко понять, что если взять приращение ЛАЧХ

L₂ (10 ω^*) – L₂ (ω^*)

и отнести его к интервалу изменения частоты, то тем самым определиться наклон асимптоты к оси частот

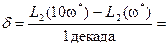
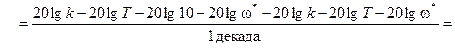
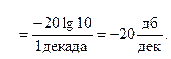
Итак, наклон второй асимптоты L₂(ω) составляет 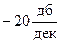, т.е. при росте частоты на 1 декаду L₂(ω) уменьшается на 20 дб.

Вообще же, чтобы не определять каждый раз подобным способом наклоны произвольной асимптоты полезно запомнить следующее правило, наклон асимптоты к оси частот определяется коэффициентом со знаком, стоящим при члене lg ω в выражении для асимптоты. Например, если

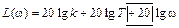
то соответствующий наклон равен 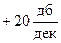, а при

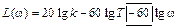
этот наклон будет .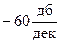

На рис. 24 изображена ЛАЧХ инерционного звена своими асимптотами

.

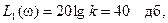
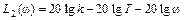Часто ЛАЧХ звена или системы характеризуют путем обозначения наклонов ее асимптот. В данном случае эта характеристика будет выглядеть так

.

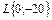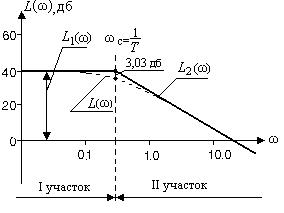
Рис.2.11. ЛАЧХ инерционного звена.

На этом же рисунке пунктиром изображена точная ЛАЧХ L(ω). Видно, что максимальная ошибка, возникающая от замены точной ЛАЧХ на асимптотическую, наблюдается на сопрягающей частоте 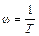и приблизительно равна 3,03 дб.

Чтобы оценить влияние параметров звена k и T на его ЛАЧХ, надо понять, что изменение k приводить к изменению 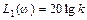. Иными словами, при изменении k первая асимптота перемещается по вертикали параллельно самой себе. Но так как конец первой асимптоты является началом второй, т.е. первая и вторая асимптоты жестко связаны, то точно такое же перемещение по вертикали будет претерпевать и вся асимптотическая ЛАЧХ.

Понятно так же, что при изменении Т меняется сопрягающая частота 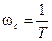. Значит, при изменении T ЛАЧХ инерционного звена будет перемещаться по горизонтали параллельно самой себе.