Основні фізичні параметри і рівняння динаміки
| Поступальний рух | Обертальний рух | |
| Основні фізичні параметри | ||
Маса 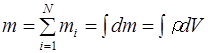
| Момент інерції
 (ІІ.2.1)
(ІІ.2.1)
| |
Імпульс
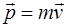
| Момент імпульсу
 (ІІ.2.2) (ІІ.2.2)
| |
Сила

| Момент сили
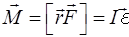 (ІІ.2.3) (ІІ.2.3)
| |
| Кінетична енергія | ||
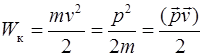
| 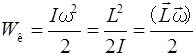 (ІІ.2.4)
(ІІ.2.4)
| |
Робота 
| ||

| 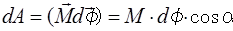 (ІІ.2.5)
(ІІ.2.5)
| |
Потужність  (ІІ.2.6) (ІІ.2.6)
| ||

| 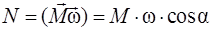 (ІІ.2.7)
(ІІ.2.7)
| |
| Основний закон динаміки | ||

| 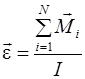 (ІІ.2.8) (ІІ.2.8)
| |

| 
| |
| Закони збереження | ||
механічної енергії
 (ІІ.2.9) (ІІ.2.9)
| ||
імпульсу

| моменту імпульсу
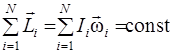 (ІІ.2.10) (ІІ.2.10)
| |
ЕЛЕМЕНТИ РЕЛЯТИВІСТСЬКОЇ МЕХАНІКИ.
НЕІНЕРЦІАЛЬНІ СИСТЕМИ ВІДЛІКУ
Принцип відносності Галилея. Перетворення
Галилея
Для рішення задач, пов’язаних із переходом від однієї системи відліку до іншої, у класичній нерелятивістській фізиці застосовується принцип відносності Галилея: всі інерційні системи повністю рівноправні щодо причин прискорень. У всіх інерційних системах відліку закони класичної механіки мають один і той же вигляд.
Роздивимося две інерціальні системи відліку. На рис. 1.5.1 представлени: К(XOY) – нерухома система координат;  (X'O'Y')– система координат, пов'язана зі спостерігачем на тілі, що переміщується щодо системи координат К(XOY).
(X'O'Y')– система координат, пов'язана зі спостерігачем на тілі, що переміщується щодо системи координат К(XOY).

Рис. 1.5.1. Рухома і нерухома системи відліку
Радіус-вектор точки М в нерухомій системі  повязаний з радіусои-вектором
повязаний з радіусои-вектором  у рухомій системі співвідношенням
у рухомій системі співвідношенням
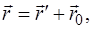 (1.5.1)
(1.5.1)
де  - радіус-вектор початку координат системи
- радіус-вектор початку координат системи  відносно системи К. Припускаючи, що система
відносно системи К. Припускаючи, що система  рухається відносно системи К з постійною швидкістю (
рухається відносно системи К з постійною швидкістю ( 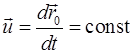 ), а також, що згідно Галилею хід часу не залежить від відносного руху систем відліку, будемо мати перетворення, які мають назву перетворень координат Галилея. В скалярній формі:
), а також, що згідно Галилею хід часу не залежить від відносного руху систем відліку, будемо мати перетворення, які мають назву перетворень координат Галилея. В скалярній формі:
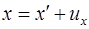
 (1.5.2)
(1.5.2)

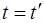
Діференцуючи рівняння (1.5.2) по часу, одержимо зв'язок між швидкостями тіл у ситемах К і  , що відомий як формула додавання швидкостей у класичній механіці
, що відомий як формула додавання швидкостей у класичній механіці
 (1.5.3)
(1.5.3)
Аналогічно, застосувавши операцію диференціювання до рівняння (1.5.3), будемо мати
 . (1.5.4)
. (1.5.4)
Відсіля витікає, що прискорення будь-якого тіла у всіх системах відліку, які рухаються друг відносно друга рівномірно і прямолінійно, виявляються одними й тими же. А поскільки основне рівнння механіки (1.2.2) вміщує тільки прискорення, то стає очевидним, що і сили, які діють на тіло у різних інерціальних системах, однакові. Тобто, рівняння класичної нерелятивістської механіки не змінюються при переході від однієї інерціальної системи до іншої, і ніякими механічними опитами неможливо встановити, знаходиться ця система в стані спокою чи рухається прямолінійно і рівномірно.
1.5.2. Спеціальна теорія відносності. Постулати
Ейнштейна
Релятивістська фізика відмовилася від трактовки Галилея часу, як абсолютно протікаючого у всіх системах. Створена А. Ейнштейном у 1905 році спеціальна теорія відносності (СТВ) пов'язала в єдине ціле простір і час. Основу цієї теорії утворюють два постулати.
Перший постулат Ейнштейна (принцип відносності).
Усі закони природи інваріантні (незмінні) стосовно переходу від однієї інерціальної системи відліку до іншої.
Перший постулат – це узагальнення принципу відносності класичної механіки (принципу відносності Галілея) на всі процеси в природі, інакше кажучи, всі інерціальні системи відліку еквівалентні (рівноправні) по своїх фізичних властивостях, тобто ніякі опити в принципі не дозволяють виділити ні одну з них як переважну – абсолютну.
Другий постулат Ейнштейна (принцип сталості швидкості світла).
Швидкість світла у вакуумі не залежить від швидкості руху джерела світла або спостерігача й однакова у всіх інерціальних системах відліку.
Другий постулат стверджує, що сталість швидкості світла – фундаментальна властивість природи. Якщо всі інші швидкості змінюються при переході від однієї інерціальної системи відліку до іншої, то швидкість світла у вакуумі – величина інваріантна (незмінна).
Всі положення СТВ базуються на експерименті і блискуче підтверджуються експериментом. Так, другий постулат А. Ейнштейн сформулював на основі опитів Майкельсона – Морлі (1881-1887 р.), які з’ясували, що немає різниці між часом розповсюдження світла паралельно і перпендикулярно к напрямку руху Землі.
Дата добавления: 2016-11-28; просмотров: 690;
