Перетворення Лоренца. Кінематичні наслідки СТВ
Аналіз постулатів СТВ свідчить, що перетворення Галилея несумістні з ними. Так, закони класичної електродинаміки, сформульовані. Дж. Максвелом, виявилися неінваріантними щодо перетворень Галилея, тобто мали різний вигляд у різних ІСВ; класичний закон додавання швидкостей не відповідав другому постулату Ейнштейна тощо.
Як було з’ясовано, перетворення, які б задовольняли постулатам СТВ, були знайдені Г.А.Лоренцом у 1904 році, але їх фізична суть була розкрита Ейнштейном.
Припустимо, що система відліку К' рухається відносно системи К зі швидкістю u, яка спрямована уздовж загальної для обох систем осі х. Тоді перехід від інерціальної системи К до іншої ІСВ К' здійснюється за допомогою перетворень Лоренца у такому вигляді
 (1.5.5)
(1.5.5)
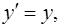
 (1.5.6)
(1.5.6)
 (1.5.7)
(1.5.7)
Перетворення Лоренца симетричні і відрізняються знаком при u, якщо роздивляється перехід від системи К' до системи К.
Перетворення Лоренца задовольняють принципу відповідності, тобто при  переходять у перетворення координат Галилея.
переходять у перетворення координат Галилея.
При 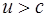 перетворення Лоренца втрачають сенс, тобто рух фізичних тіл із швидкістю, що перебільшує швидкість світла неможливий.
перетворення Лоренца втрачають сенс, тобто рух фізичних тіл із швидкістю, що перебільшує швидкість світла неможливий.
Просторові і часові перетворення не являються незалежними. Перетворення Лоренца зв’язують просторові координати і час в одне нерозривне ціле, утворюючи так званий чотиривимірний простір-час.
Перерахуємо наслідки, які випливають із перетворень Лоренца.
Відносність одночасності.
Роздивимось випадок, коли у системі К дві події А и В відбуваються в одній і тій же точці (хА = хВ) одночасно (tA = tB). Для даних умов, відповідно до перетворень Лоренца, х'А = х'B і t'A = t'B, тобто ці події в системі К' є одночасними й просторово співпадаючими.
Якщо в системі K події просторово роз'єднані (хА ≠ хB), але одночасні (tА = tB), то, відповідно до перетворень Лоренца, ці події в системі К', залишаючись просторово роз'єднаними (  ), виявляються й неодночасними (
), виявляються й неодночасними ( 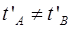 ).
).
Поняття одночасності подій відносні, тобто залежить від системи відліку.
Довжина тіл у різних системах відліку (лоренцеве скорочення довжини).
Нехай тіло (стрижень) рухється разом з системою К' відносно системи К. з швидкістю u вздовж осі х. В системі відліку К', щодо якої стрижень покоїться, його власна довжина 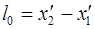 (стрижень розташований уздовж осі х). Згідно перетворень Лоренца в системі К, щодо якої стрижень рухається його довжина
(стрижень розташований уздовж осі х). Згідно перетворень Лоренца в системі К, щодо якої стрижень рухається його довжина
 (1.5.8)
(1.5.8)
Таким чином, довжина стрижня, що рухається, менше довжини, обмірюваної в системі, щодо якої він знаходиться у спокої (менше власної довжини) і в різних інерціальних системах відліку різна. Із рівнянь (1.5.3) виходить, що поперечні розміри тіла не залежить від швидкості руху й однакові у всіх інерціальних системах відліку.
Лоренцеве скорочення довжини – ефект кінематичний і взаємний: якщо в системах К и К' є два однакових стрижні, то з погляду кожної з них коротше той стрижень, що рухається щодо неї.
Тривалість подій у різних системах відліку (релятивістське вповільнення часу).
Якщо в системі відліку К' (вона рухається щодо системи К зі швидкістю u вздовж осі х) інтервал часу між двома подіями, що відбуваються в одній і тій же точці, дорівнює  , то інтервал часу між цими подіями в системі К (
, то інтервал часу між цими подіями в системі К (  ) згідно перетворень Лоренца дорівнює
) згідно перетворень Лоренца дорівнює
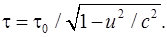 (1.5.9)
(1.5.9)
Таким чином, тривалість події, що відбувається в деякій точці, найменша в тієї інерціальній системі відліку, щодо якої ця система нерухлива. Отже, годинники, що рухаються відносно інерціальної системи відліку, ідуть повільніше годинників, що знаходяться у спокої.
Цей ефект кінематичний і взаємний: якщо з точки погляду K-cистеми повільніше йдуть годинники К'-системи, то з точки погляду К'-системи, навпаки, повільніше йдуть годинники К-системи (причому в тім же відношенні).
Релятивістський закон додавання швидкостей.
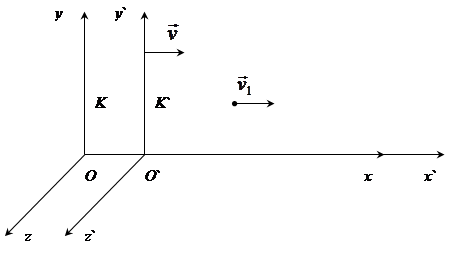
Рис. 1.5.2. Рух тіла у системах відліку К і К'
Нехай тіло рухається уздовж осі х' К'-системи зі швидкістю v1 (рис. 1.5.2). В свою чергу система К' рухається щодо системи К зі швидкістю u. Вісі х і х' збігаються, а вісі y і у', z і z' паралельні. Із перетворень Лоренца отримуємо:
 (1.5.10)
(1.5.10)
де v1 – швидкість тіла відносно К'; v2 – швидкість цього ж тіла відносно К.
Якщо u<<с і  , то
, то
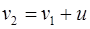 (1.5.11)
(1.5.11)
і ми маємо закон додавання швидкостей у класичній механіці.
Якщо світловий імпульс у К'-cистемі рухається уздовж вісі x' зі швидкістю 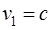 , то в системі відліку K
, то в системі відліку K
 (1.5.12)
(1.5.12)
Дата добавления: 2016-11-28; просмотров: 1900;
