Глава 7.Правило сложения дисперсий

Если данные представлены в виде аналитической группировки, то можно исчислить:

1. Общую дисперсию;

2. Межгрупповую;

3. Внутригрупповую.

1. Измеряем вариацию признака по всей совокупности под влиянием всех факторов, обуславливающих эту совокупность.

2. Характеризуем системную вариацию, т.е. различия в величине изучаемого признака, возникаемого под влиянием факторов признака, положенного в основание.

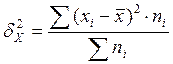
3. Отражает случайную вариацию, т.е. вариацию, происходящую под влиянием случайных факторов.

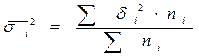
Существует закон дисперсии:

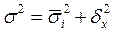(правило сложения дисперсий).

Выяснение общего характера распределения предполагает не только оценку степени его однородности, но и оценку симметричности.

Симметричным называется распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения равны между собой.

В статистике для характеристики асимметрии используется следующие показатели:

1. Асимметрии;

2. Эксцесса.

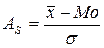
При симметрическом ряде распределения 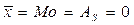, если A_S>0, то правосторонняя асимметрия, т.к. .

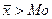Если А_S<0, то левосторонняя асимметрия.

-3< А_S<3

В практических расчетах используется следующая формула:

,

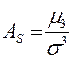где 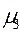- центральный момент третьего порядка, 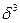- средняя квадратическая ряда.

Если А_S>0.5 – значительная асимметрия, А_S<0.25 – незначительная асимметрия.

Для характеристики структуры вариационных рядов применяются структурные характеристики.

Мода наиболее часто встречающееся значение признака в исследуемой совокупности.