Глава 10.Экономические индексы

Экономический индекс – это относительная величина, которая характеризует изменение исследуемого явления во времени, в пространстве, с некоторым эталоном (плановый, нормативный, предыдущий уровень и т.д.).

Индивидуальный индекс характеризует изменение во времени отдельных элементов совокупности, индивидуальный индекс цены, рассчитывается по формуле:

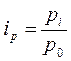, где p_i – цена в текущем периоде, p₀ – цена в базовом периоде.

Например, p_i =30, p₀ =25

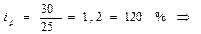цена по сравнению с базисным уровнем увеличилось на 20%.

Индивидуальный индекс физического объема реализации:

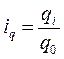, где q_i –количество товара, реализованного в текущем году, q₀ – количество товара, реализованного в базовом году.

Индивидуальный индекс товарооборота:

i_pq =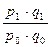

Сводный индекс – это относительный показатель, который характеризует среднее изменение социально-экономического явления состоящего из несоизмеримых показателей.

Сводный индекс товарооборота рассчитывается по следующей формуле:

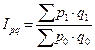
Сводный индекс цен:

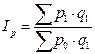
Количество (веса) фиксируются на постоянном уровне. При исследовании динамики таких показателей как P-цена, Z-себестоимость, W-урожайность, количественный показатель характеризуется текущим уровнем.

Сводный индекс физического объема реализации:

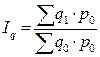
Весом является цена, которая фиксируется на базисном уровне.

Между индексами существует следующая взаимосвязь:

.

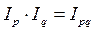
Мы рассмотрели применение агрегатных индексов в анализе товарооборота и цен. При анализе результатов производственной деятельности промышленного предприятия приведенные выше сводные индексы соответственно называются индексом стоимости продукции, индексом оптовых цен и индексом физического объема продукции.

Рассмотрим применение индексного метода в анализе изменения затрат на производство и себестоимости продукции.

Индивидуальный индекс себестоимости характеризует изменение себестоимости отдельного вида продукции в текущем периоде по сравнению с базисным:

.

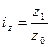Для определения общего изменения уровня себестоимости нескольких видов продукции, выпускаемых предприятием, рассчитывается сводный индекс себестоимости. При этом себестоимость взвешивается по объему производства отдельных видов продукции текущего периода:

.

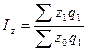Числитель этого индекса отражает затраты на производство текущего периода, а знаменатель – условную величину затрат при сохранении себестоимости на базисном уровне. Разность числителя и знаменателя показывает сумму экономии предприятия от снижения себестоимости:

.

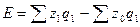Сводный индекс физического объема продукции, взвешенный по себестоимости. имеет следующий вид:

.

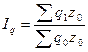Третьим показателем в данной индексной системе является сводный индекс затрат на производство:

.

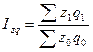Все три индекса взаимосвязаны между собой:

.

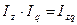Еще одна область применения индексного метода- анализ изменений в производительности труда. При этом возможны два подхода к расчету индексов. Первый подход основан на учете количества продукции, вырабатываемого в единицу времени (w).

При таких расчетах необходимо решить ряд методологических проблем, – какой именно показатель продукции использовать, как оценить продукцию работников сферы услуг и пр.

При втором подходе производительность труда определяется затратами рабочего времени на единицу продукции (t). На практике эти расчеты также сопряжены с определенными трудностями, так как не всегда имеется возможность оценить вклад конкретного работника в производство того или иного изделия.

Количество продукции, вырабатываемое в единицу времени (в натуральном выражении), и затраты времени на единицу продукции взаимосвязаны между собой:

.

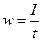Например, если работник на каждое изделие затрачивает 15 мин. (t=0,25 ч), то за час его выработка составит 4 изделия. Отметим, что выработка может измеряться не только в натуральном, но в стоимостном выражении (pq).

Индивидуальные индексы производительности труда, основанные на этих показателях, имеют следующий вид:

;

,

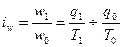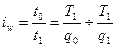где T - суммарные затраты времени на выпуск данной продукции в человеко-часах, человеко-днях или человеко-месяцах (в последнем случае соответствует общей численности работников).

Трудоемкость является обратным показателем, поэтому снижение трудоемкости в текущем периоде по сравнению с базисным свидетельствует о росте производительности труда.

Располагая данными о трудоемкости различных видов продукции и объемах их производства, можно рассчитать сводный индекс производительности труда (по трудоемкости):

.

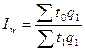Знаменатель этого индекса отражает реально имевшие место общие затраты времени на выпуск всей продукции в текущем периоде (T₁). Числитель представляет собой условную величину показывающую, какими были бы затраты времени на выпуск этой продукции, если бы трудоемкость не изменилась.

Индекс производительности труда по трудоемкости связан с индексом затрат рабочего времени (труда) и с индексом физического объема продукции, взвешенным по трудоемкости:

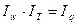
или

.

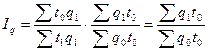При расчете сводного индекса производительности труда в стоимостном выражении (по выработке) необходимо количество продукции, произведенной за каждый период, взвесить по каким-либо ценам, принятым за сопоставимые. В качестве сопоставимых могут выступать цены текущего, базисного или какого-либо другого периода или средние цены. Индекс в этом варианте рассчитывается по формуле:

.

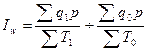Первая часть этой формулы представляет собой среднюю выработку в отчетном периоде, вторая часть – в базисном.

Умножение индекса производительности труда по выработке на индекс затрат рабочего времени приводит к индексу физического объема продукции, взвешенному по цене:

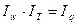
или

.

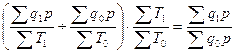Сводные индексы в средней арифметической и средней гармонической формах. В ряде случаев на практике вместо индексов в агрегатной форме удобнее использовать средние арифметические и средние гармонические индексы. Любой сводный индекс можно представить как среднюю взвешенную из индивидуальных индексов. Однако при этом форму средней нужно выбрать таким образом, чтобы полученный средний индекс был тождественен исходному агрегатному индексу.

Предположим, мы располагаем данными о стоимости проданной продукции в текущем периоде (p₁q₁) и индивидуальными индексами цен 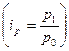, полученными, например, в результате выборочного наблюдения. Тогда в знаменателе сводного индекса цен 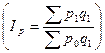можно использовать следующую замену:

.

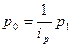Таким образом, сводный индекс цен будет выражен в форме средней гармонической из индивидуальных индексов:

.

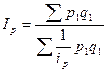Индексы постоянного и переменного состава. Все рассмотренные выше индексы рассчитывались по нескольким товарам, реализуемым в одном месте, или видам продукции, производимым на одном предприятии. Рассмотрим теперь случай, когда один товар реализуется в нескольких местах или вид продукции производится на ряде предприятий.

Если реализуется только один вид продукции, вполне правомерно рассчитать его среднюю цену в каждом периоде. Индекс переменного состава представляет собой отношение двух полученных средних значений:

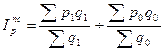
Данный индекс характеризует не только изменение индивидуальных цен в местах продажи, но и изменение структуры реализации по предприятиям розничной или оптовой торговли, рынкам, городам, регионам. Для оценки воздействия этого фактора рассчитывается индекс структурных сдвигов:

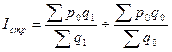
Последним в данной системе является рассмотренный выше индекс цен фиксированного состава, который не учитывает изменение структуры:

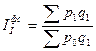
Между данными индексами существует следующая взаимосвязь:

.

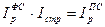Такое несоответствие объясняется влиянием изменения структуры реализации товаров по регионам: в июне по более высокой цене продавали товара вдвое больше, в июле же ситуация принципиально изменилась (в данном условном примере для наглядности числа подобраны таким образом, чтобы это различие в структуре продаж было очевидным).

Рассчитаем индекс структурных сдвигов:

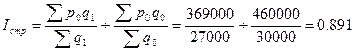, или 89,1%.

Первая часть этого выражения позволяет ответить на вопрос, какой была бы средняя цена в июле, если бы цены в каждом регионе сохранялись на прежнем июньском уровне. вторая часть отражает фактическую среднюю цену июня. В целом по полученному значению индекса мы можем сделать вывод, что за счет структурных сдвигов цены снизились на 10,9%.

Рассчитанный индекс цен фиксированного состава равен 1,098, или 109,8%. Отсюда следует вывод: если бы структура реализации товара А по регионам не изменилась, средняя цена возросла бы на 9,8%. Однако влияние на среднюю цену первого фактора оказалось сильнее, что отражается в следующей взаимосвязи:

1,098*0,891=0,978.

Аналогично строятся индексы структурных сдвигов, переменного и фиксированного составов для анализа изменения себестоимости, урожайности и пр.