Приемы обработки и анализа ряда динамики
При анализе рядов динамики иногда возникает необходимость смыкания рядов, т.е. объединение двух и более рядов динамики в один ряд.
Существует несколько способов приведения ряда динамики к сопоставимому виду.
1. Смыкание рядов, т.е. объединение двух или более рядов, характеризующих изменение явления, в один ряд.
2. Заключается в том, что уровни года, в котором произошли изменения принимаются за 100%, а остальное пересчитывается по отношению к этим уровням соответственно.
Получен сопоставимый ряд динамики общего объема продукции промышленности (в новых границах)
| Годы | |||||||
| 22,5 | 23,2 | 23,5 | 23,8 | 24,6 | 25,5 | 27,2 |
Другой способ смыкания. Применив другой способ смыкания получим следующий ряд динамики, характеризующий объем продукции.
| Годы | |||||||
| Общий объем продукции в новых границах (% к 2004г.) | 94,8 | 97,6 | 99,1 | 103,4 | 107,2 | 114,3 |
При изучении в рядах динамики основной тенденцией развития явления принимаются различные приемы и методы.
1. Один из приемов выявления основной тенденции.
Этот способ основан на укрупнении периодов времени, к которым относятся уровни ряда динамики.
Например, ежесуточный выпуск продукции заменяется рядом месячного выпуска.
2. Метод скользящей средней.
Суть состоит в замене абсолютной величины средними арифметическими за определенные периоды. Расчет средней ведется способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего.
3. Приведение ряда динамики к общему основанию.
Например.
По исходным уровням нескольких рядов динамики определяются относительные величины – базисные темпы роста и прироста. принятый при этом за базу сравнения период (момент) времени выступает в качестве постоянной базы расчета темпов роста для каждого из изучаемых рядов динамики.
При анализе ряда динамики важное значение имеет выявление сезонных колебаний. Этим колебаниям свойственны устойчивые изменения уровней ряда по внутригодовым периодам: месяцам, кварталам. Для выявления сезонных колебаний анализируется месячные и квартальные уровни ряда динамики за год и за несколько лет.
Используется индекс сезонности – IS.
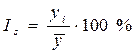
и т.д.
На практике для выявления закономерностей колебаний пользуются месячными данными за несколько лет (не менее 3 лет). Тогда для каждого месяца рассчитывается средняя величина уровня за 3 года, затем рассчитывается средний месячный уровень для всего ряда и в заключении определяется процентное соотношение средних для каждого месяца к общему средне-месячному уровню ряда, т.е.

 , где
, где
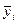 - среднее для каждого месяца за 3 года;
- среднее для каждого месяца за 3 года;
 - общий средний месячный уровень за 3 года.
- общий средний месячный уровень за 3 года.
Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание. При этом уровни ряда динамики выражаются в виде функции времени: 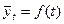 .
.
Аналитическое выравнивание может быть осуществлено по любому рациональному многочлену. Выбор функции производится на основе анализа характера закономерностей динамики данного явления.
Рассмотрим применение метода аналитического выравнивания по прямой для выражения основной тенденции на следующем примере.
В таблице 1 приведены исходные и расчетные данные о динамике производства молока в регионе за 1993-1997 гг.
Исходные и расчетные данные для определения параметров системы уравнения
(млн. т)
| Годы | Млн т | t | t2 | ty | 
| 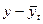
| 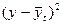
|
| 13,3 | -2 | -26,6 | 13,02 | 0,28 | 0,08 | ||
| 13,5 | -1 | -13,5 | 13,94 | -0,44 | 0,19 | ||
| 14,8 | 14,86 | -0,0 | 0,00 | ||||
| 16,1 | 16,1 | 15,78 | -0,32 | 0,10 | |||
| 16,6 | 33,2 | 16,70 | -0,1 | 0,01 | |||
| Итого | 74,3 | - | 9,2 | 74,30 | - | 0,38 |
Для выравнивания ряда динамики по прямой используем уравнение 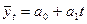 .
.
Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров а0 и а1:
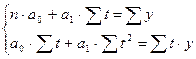
где y – исходный уровень ряда динамики;
n – число членов ряда;
t – показатель времени, который обозначается порядковыми номерами, начиная от низшего. Например:
| Годы | |||||
| t |
Решение системы уравнений позволяет получить выражения для параметров а0 и а1
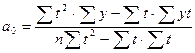 ;
;
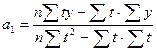 .
.
В рядах динамики техника расчета параметров уравнения может быть упрощена. Для этой цели показателем времени t придают такие значения, чтобы их сумма была равна нулю, т.е.  . В нашем примере число исходных уравнений системы примут следующий вид:
. В нашем примере число исходных уравнений системы примут следующий вид:
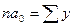 и
и 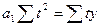 ,
,
откуда: 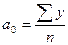 представляет собой средний уровень ряда динамики (
представляет собой средний уровень ряда динамики (  );
);
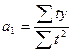 .
.
Однако если число уровней ряда четное, то условное обозначение показателя времени принимает следующий вид:
| Годы | ||||||
| t | -5 | -3 | -1 | +1 | +3 | +5 |
(это означает, что счет времени ведется полугодиями).
Основная тенденция (трен) показывает, как воздействуют систематические факторы на уровень ряда динамики, а колеблемость уровней около тренда служит мерой воздействия остаточных факторов. Ее можно измерить по формуле
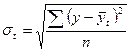 - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
Используя данные этого примера, рассчитаем показатель колеблемости производства молока в регионе
Дата добавления: 2016-11-02; просмотров: 1033;
