Алгоритм предварительной обработки данных

1. Постановка задачи.

Исходные данные.

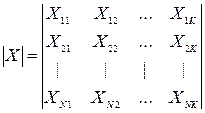- матрица (n x k.) - план эксперимента.

X – большие, т.к. замеры получаем в конкретных физических единицах (не безразмерные).

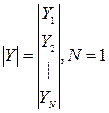
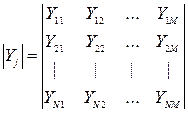- матрица (NxM).

В каждом эксперименте последовательность опытов (в столбцах) отличается друг от друга и носит рандомизированный характер (случайный). Это делается для снижения монотонного накопления шумовых воздействий.

За счет рандомизации – рассеяние однородное.

В Y – матрице строка является распределением экспериментальных данных, которое может носить и теоретический и экспериментальный характер (эмпирическое распределение дисперсии).

Необходимо определить наличие выбросов аномальных измерений Y, нарушение условий проведения опытов и нормальных распределений данных в каждой строке (Y*м).

2. Этапы предварительной обработки данных.

1). Расчет эмпирических средних по строкам:

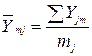- построчное среднее

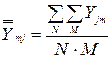- среднее по эксперименту

2) Дисперсия воспроизводимости, построчная дисперсия:

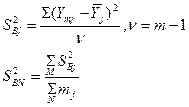
При подсчете среднего значения первая степень свободы считается уже использованной, поэтому в знаменателе (m-1).

Эта дисперсия показывает характеристики рассеивания экспериментальных данных в каждом опыте. Чем она меньше, тем меньше влияние побочных эффектов и выше точность оценки выходного параметра. Некоторые физические эксперименты являются не воспроизводимыми, т.е. их повтор невозможен (например, летные испытания на природе).

3) Определение статистической однородности дисперсии воспроизводимости:

Статистический нуль → гипотезы → H₀

Критерий Фишера:

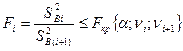
В каждой использованной строке считается эмпирическая дисперсия и определяется их соотношение.

H₀: Если расчетное значений меньше табличного (определенного по α,ν_i,ν_i+1), то считаются дисперсии однородными на заданном уровне вероятности α (α=1-p, где p - вероятность).

В том случае, если устанавливается неоднородность, то это означает, что в одном из распределений присутствует выброс или при проведении экспериментов не учтен существенный фактор (либо просто грубая ошибка).

4) Оценка отклонений от среднего:

H₀: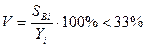

Если условие нарушается, то это означает присутствие выброса или неустановленного существенного фактора (например, изменение температуры и давления на улице → в лаборатории).

5) Оценка отклонений среднего по Т-критерию:

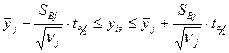: H₀

t - критерий Стьюдента, используемый для оценки распределения экспериментальных данных при малом количестве измерений.

t определяется по таблице по величине α (достоверности) и количеству экспериментальных данных.

H₀: Если экспериментальные данные в первой выборке удовлетворяют значению неравенства, то они считаются однородными и не имеют выбросов.

6) Оценка однородности дисперсии воспроизводимости по x²-критерию:

H₀: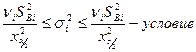

Дисперсия σ_i считается по каждому из опытов однородной, если удовлетворяет неравенству, т.е. находится в диапазоне установленным x²-критерием. В противном случае, σ_i, неудовлетворяет неравенству, считается неоднородной, и в этом опыте необходимо выявить выброс или дополнительное воздействие неучтенных факторов.

7) Проверка нормальности распределения экспериментальных данных по условиям каждого опыта:

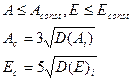
Рис.50. Проверка нормальности

q –число данных в первой выборке

M{Y_j} – математическое ожидание истинного значения выходного параметра

p – вероятность попадания параметра в интервал

3σ – утроенное значение дисперсии выходного параметра

Значение p может варьироваться в интервале от 0,90 до 0,99. «Хвосты» могут быть тяжелыми и нормальными.

Н₀: А_с – ассиметрия.

Н₀: Е_с - эксцентриситет

Ассиметрия рассчитывается по табличным данным (дисперсионная симметрия).

Если первичная обработка данных не устанавливает выбросов и отклонений от нормальности распределения, считается возможным применять на этапе вторичной обработки метод наименьших квадратов для расчета значений коэффициентов регрессионного уравнения.

Если нормированность не устанавливается, то применяется для расчетов b_i: обобщенный метод наименьших квадратов; устойчивые методы обработки.