Типы регрессионных моделей

Рис.29. Схема «объект»
1. Однофакторная линейная
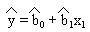 ,
,
где bо - свободный член, b1- линейные коэффициенты уравнения, xi- факторы, ˆ - величина оценочная, приближенная.
Регрессионная модель позволяет обеспечить простую графическую интерпретацию и учет взаимовлияния пар факторов, что отличает Регрессионную модель от других математических моделей.
2. Двухфакторная:
а) линейная
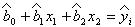
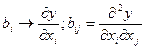 скорость
скорость
б) нелинейная
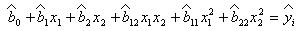
3. Многофакторная
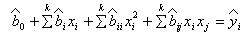
Регрессивное уравнение имеет члены позволяющие оценить эффекты взаимодействия факторов двойные, тройные и т.д. в зависимости от числа факторов модели. Эффект парных взаимодействий факторов зачастую оказывается более сильный чем одинарный эффект, поэтому эти модели в данном случае имеют очень большое значение для расшифровки влияния факторов на выходной параметр объекта. Математически каждый из коэффициентов регрессивного уравнения математически интегрируется как частная производная выходного параметра по каждому фактору.
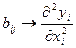 (ускорение)
(ускорение)
2. Определение интервала, диапазона Xi

Рис.30. Координатная ось для безразмерного обозначения фактора
I = Xiв(н) –Xi0; D = Xiв –Xiн
Безразмерное обозначение Xi: Xiн = -1, Xi0 = 0, Xiв = +1, I = 1, D = 2.
Для проведения эксперимента устанавливается диапазон входных воздействий, который определяется инструментом и фиксируется в программе (на шкалах инструмента).
Xi0= 0 не значит, что значение фактора в этой точке равно нулю, это просто центр нашего интервала в физических параметрах Паскалях. Операция перехода к безразмерным обозначениям факторов обеспечивает центрирование (это перенос из физического нуля в середину интервала измерения фактора) и нормирование (установление новой нормы для всех факторов, все факторы изменяются от нижнего уровня -1 до верхнего уровня +1) системы факторов. Такой подход позволяет оперировать в уравнении только значениями коэффициентов, что значительно упрощает порядок расчетов. При этом Xi безразмерная величина, а коэффициенты имеют размерность выходного параметра. По значениям коэффициентов и их величине в данном случае можно давать оценку относительной силы влияния одного фактора перед другими если уравнение многофакторное.
Выбор плана эксперимента. Типы планов экспериментальных исследований
Вид выбранной математической модели определяет план экспериментальных исследований.
Планы в регрессионном анализе имеют два вида: линейные и нелинейные. Насчитывается несколько тысяч планов (выбор по каталогам). Математические регрессионные модели диометрически интерпретируются в виде зависимости соответствующего характера линейного или нелинейного.
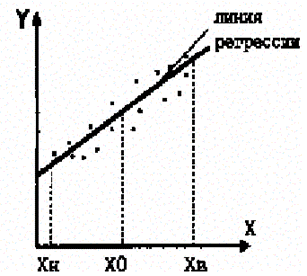
Рис.31. График линии регрессии
Алгоритм плана ПЭ:
1. выбор по определенным данным xi который будет меняться в эксперименте хi+1-const, A-var, В – const.
2. проведение эксперимента из m опытов и n повторов (соблюдение принципа рандомизации)
Однофакторная линейная модель
В процессе экспериментов экспериментальные значения параметров колебляться вокруг линии регрессии, линия метаматематического ожидания в облаке экспериментальных точек.
Типы планов экспериментов:
1 .Классические
2. Латинские
3. Греко-латинские
4. Гипер-греко-латинские
5. Комбинированные
6. Активного эксперимента, на основе матрицы Адамара
7. Планы классического эксперимента
Классический план эксперимента
При оном или двух воздействиях на объект используется метод последовательного измерения входных воздействий по заранее выбранным уровням и измерениям соответственно.
План последовательного эксперимента используется для построения монограмм. Yj; x1 -А; x2-В; m=3 - число уровней

Рис.32 График факторов A, B
Алгоритм плана ПЭ:
1. Выбор по определенным данным Xi, который будет меняться в эксперименте Xi+1- const, А – const.
2. Проведение эксперимента из m опытов и n повторов(соблюдение принципа рандомизации).
3. Графическая интерпретация.
4. Интерация по 1-3(повтор операций)
Таблица 9
| A B | A1 | A2 | A3 |
| B1 | α | ||
| B2 | α | ||
| B3 | α |
Минусы классического плана:
- невозможна оценка взаимодействия факторов;
- большая погрешность полученного результата;
- отсутствие возможности исследования многофакторного процесса.
Сеть графиков выполненных при изменении одного из факторов при постоянном уровне второго будет называться монограммами, служат они для оценки поведения фактора.
Опыт - это одно испытание, связанное с изменением выходного параметра. Недостаток классического плана - большое количество экспериментов.
Латинские планы
Определяются обозначением факторов латинскими буквами. Применяются для оценки статистических характеристик воздействия факторов на объект (оценки их дисперсионных характеристик и оценки их ранга относительно друг друга).
Цель:
1. Оценка существенности воздействий xi (А, В);
2. Оценка преимущественного воздействия А относительно В и наоборот. Для достоверности статистических оценок необходимо проводить 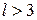 . Эксперимент заключается в проведении опыта в каждой точке плана независимо от изменения фактора по уровням, т.е. с учетом принципа рандомизации. Принцип рандомизации - это принцип случайного чередования опытов, применяется для избежания эффекта влияния изменения фактора от нижнего к верхнему или наоборот, выполняется по генераторам случайных чисел или по математическим таблицам.
. Эксперимент заключается в проведении опыта в каждой точке плана независимо от изменения фактора по уровням, т.е. с учетом принципа рандомизации. Принцип рандомизации - это принцип случайного чередования опытов, применяется для избежания эффекта влияния изменения фактора от нижнего к верхнему или наоборот, выполняется по генераторам случайных чисел или по математическим таблицам.
Латинский план АхВ – двухфакторный
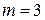 - число уровней
- число уровней
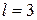 - число повторов опытов
- число повторов опытов
Таблица 10
| A B | A1 | A2 | A3 |
| B1 | Y1 | Y4 | Y7 |
| B2 | Y2 | Y5 | Y8 |
| B3 | Y3 | Y6 | Y9 |
(Сводим факторы B2 и A3 и замеряем выходной параметр Y8)
Алгоритм экспериментальных исследований с латинским квадратом
1. Xi, пределы Yi.
2. Рандомизированная последовательность опытов n в эксперименте Qi.
Для определения статистических характеристик эксперимента в отдельных случаях возможно проведение опытов только в одной точке плана и далее условно рассчитанные показатели распределяются на все точки плана.
3. Проведение эксперимента.
4. Обработка данных (для каждого последовательного эксперимента можно построить кривую Гаусса).
Экспериментальная дисперсия So, SA, SB, s.
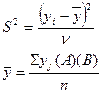
n –число опытов в 1-ой точке плана ≥ 3.
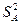 ,
, 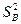
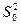 - в числителе среднее считается по горизонтали по уровню фактора A (SA), по вертикали – B (SB), по всем опытам - So.
- в числителе среднее считается по горизонтали по уровню фактора A (SA), по вертикали – B (SB), по всем опытам - So.
близка к шумовой, поэтому с ней сравниваются и. Если SA,SB > So, то они считаются существенными.
5. Оценка влияния Xi.
Средняя дисперсия (Критерий Фишера)
Но – нулевая гипотеза, в которой считаются критерии Фишера.
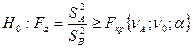
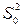 -
- 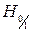 нулевые гипотезы
нулевые гипотезы
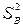 -
- 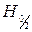
Устанавливается значимость фактора А на заданном уровне вероятности a, если Fa ≥ Fкр (Fкр по таблице)
a - степень достоверности: a =1 – P.
Латинский план позволяет определить:
- существенные факторы;
- провести их ранжирование;
- дисперсионные характеристики.
Для техники принимается Р=0,99 - 1 - уровень технической отработки объекта;
Р=0,95 -2 - экспериментальные лабораторные исследования;
Р=0,90 - 3 - лаборатории и предварительный эксперимент;
Р=0,75 - 4 - первичные испытания новых объектов;
Р=0,5 - 5 - отработка объектов и математических моделей.
По значению F можно определить вероятное преимущество одного фактора перед другим.
Греко-латинские планы
В этих планах к латинским обозначениям прибавляются греческие буквы (3-х факторные планы).
Построим план АхВхa,
m=3
l=3
Такие планы позволяют значительно сократить число опытов так для трех факторов на 3 уровне 27 опытов для классического плана.
Алгопитм аналогичен латинскому
Таблица 11
| А В | A1 | A2 | A3 |
| B1 | a1 Y1 | a2 Y4 | a3 Y7 |
| B2 | a2 Y2 | a3 Y5 | a1 Y8 |
| B3 | a3 Y3 | a1 Y6 | a2 Y9 |
ai смещены, чтобы не было повторов.
Определяем соответствие эмпирических зависимостей:
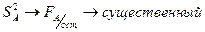
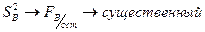
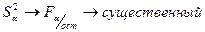
Можно определять по критерию Фишера 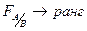 .
.
Например, H0 – нулевая гипотеза, которая позволяет определить критерии Фишера:
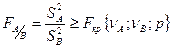 ,
,
где νА, νВ – статистические степени свободы, р – вероятность для данного случая (из списка типовых).
Греко-латинские планы имеют преимущество перед классич. В сокращении числа опытов в 3 раза, как и перед латинскими планами.
Преимущества ГЛП:
- определяются существенные факторы;
- определяется ранг;
- сокращается число опытов.
Гипер-греко-латинский план (ГГЛП)
ГГЛП - планы АхВхaхb
m=3; к=4; l=3.
Используются при числе факторов более 4.
Цель:
1. Оценка существенности воздействий хi, (A,B, a, b);
2 .Оценка преимущественного воздействия хi, ранжирование xi. При построении плана необходимо учитывать исходя из априорных данных взаимные влияния факторов на различных уровнях, целесообразно избегать сочетания факторов на mах и min уровнях.
Таблица 12
| А В | A1 | A2 | A3 |
| B1 | γ3 a1 Y1 | γ1 a2 Y4 | γ2 a3 Y7 |
| B2 | γ1 a2 Y2 | γ2 a3 Y5 | γ3 a1 Y8 |
| B3 | γ2 a3 Y3 | γ3 a1 Y6 | γ1 a2 Y9 |
ГГЛП позволяет определить существенность факторов и их ранжирование на заданном уровне вероятности.
Комбинационные планы
Являются сочетанием классического и ГГЛП, позволяют наравне с дисперсионными характеристиками выявить математические модели и провести их графо-аналитические исследования.
Если число уровней по факторам одинаково, то получаются комбинационные квадраты (КК), если различны, то получаются комбинационные прямоугольники.
Эти планы позволяют оценить статистические характеристики объекта, а также определить функциональные зависимости (многофакторные) и построить графические зависимости. При построении таких планов необходимо стремиться к тому, чтобы число уровней было нечетным, но симметричным.
В комбинационных квадратах происходит частичное заполнение клеток (Тьюарсон).
Используя КК можно вывести чистые аналитические зависимости по каждому фактору.
Пример комбинационного квадрата:
k=4, (4-х факторный), {A, B, C, D}
m=3 (число уровней), n=9 (от ГЛП)
Симметричные строки и соответственно число факторов в них 2, 4, 6 и т.д.
Х1=А; Х2=В;Х3=С; Х4=D
Таблица 13
| C1 | C2 | C3 | ||||||||
| A1 | A2 | A3 | A1 | A2 | A3 | A1 | A2 | A3 | ||
| D1 | B1 | |||||||||
| B2 | ||||||||||
| B3 | ||||||||||
| D2 | B1 | |||||||||
| B2 | ||||||||||
| B3 | ||||||||||
| D3 | B1 | |||||||||
| B2 | ||||||||||
| B3 |
Такая структура плана позволяет сократить число опытов благодаря тому, что в этом плане будут пропущены часть точек эксперимента рассчитанных по определенной формуле.
Заполнение производится по вспомогательному квадрату.
Таблица 14. Вспомогательный квадрат
В клетках проставлены номера опытов, занесение опытов из дополнительного квадрата в основной производится по вертикали, либо по горизонтали, либо по диагонали. Этот комбинационный квадрат показывает сколько опытов будет с помощью него проведено. Число опытов = 9, а в классическом плане = 81.
Для того, чтобы выбрать способ заполнения опытов в комбинационном квадрате необходим априорный анализ. При заполнении необходимо контролировать заполнение строк и столбцов только одним опытом. Опыт №4 означает что он проводится при A1, В2, С2, Д1 следовательно, когда выставлены данные уровни факторов замеряется выходной параметр, который в последствии заносится в таблицу. В каждой точке плана не менее 3 факторов. После заполнения комбинационного квадрата производится графическая интерпретация (для каждой пары факторов составляется свой комбинационный прямоугольник).
Таблица 15
| A1 | A2 | A3 | |
| D1 | Y1Y4Y7 | ||
| D2 | Y2Y5Y8 | ||
| D3 | Y3Y6Y9 |
Алгоритм метода:
1. Построение yj=f(xi), k = 4.
Зависимости строятся по принципу классического эксперимента. Выбирается наиболее сильная зависимость с наиболее «сильным» фактором, к примеру, фактору А. Зависимости могут быть нелинейными.

Рис.33. График функции по четырем факторам.
2. Определение Dy = max по xi. A→Dymax
3. Определение DyА/δ

Рис.34. Ось координат фактора А
δА→±δy
4. Компенсация влияния А (нейтрализация факторов): +δ; -δ.
Таблица 16
| A1 | A2 | A3 | |
| D1 | Y1 | ||
| D2 | Y5 | ||
| D3 | Y9 | ||
| +δ | -δ |
Затем:

Рис.35. График функции по фактору А
После нейтрализации фактора А другие факторы проявляют своё чистое воздействие (АС, АВ).
5. Пересчет значений y по другим параметрам факторов и перестроение графиков зависимостей.
6. Выявление следующего фактора с наибольшим градиентом и по y и его нейтрализация и т.д.
Выявленный на предыдущем этапе фактор компенсирован и выявляется новый сильный фактор и далее действие повторяется по нейтрализации этого фактора и т.д. Таким образом, в результате применения получаются аналитические однофакторные зависимости, которые отражают влияние xi на выходной параметр. При завершении алгоритма получаем комбинацию четырех аналитических зависимостей.
С помощью комбинационного плана получают:
1. дисперсионные характеристики;
2. ранжирование факторов;
3. аналитические зависимости «очищенных» влияний xi на y;
4. графики функций y = f(xi)
Планы на основе матрицы Адамара
Они позволяют сократить количество опытов, упростить организацию и проведение, получить математическое описание и графическую интерпретацию исследуемых процессов. Провести исследование и получить математическую модель для объектов и процессов, не имеющих такого описания в априорном анализе, т.е. представляют собой черный или серый ящик. Эти планы определяются типом выбранной математической модели (регрессионной), они делятся на планы 1-го и 2-го порядка, 1-го порядка – линейные, а 2-го - квадратичные и т.д.
Классификация планов:
1. Первого порядка
2. Второго порядка
3. Более второго порядка
Планы 1-го порядка.
Планы ПЭФ (полного факторного эксперимента) и ДФЭ (дробного факторного эксперимента).
План полного факторного эксперимента (ПФЭ)
N=mk, где m - число уровней факторов ( m=2 только в линейном случае); k - число факторов. N – число опытов.
Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом. Если число уровней каждого фактора равно двум, то имеем полный факторный эксперимент типа 2k.
Нетрудно написать все сочетания уровней в эксперименте с двумя факторами. В планировании эксперимента используются кодированные значения факторов: +1 и -1 (часто для простоты записи единицы опускают). Условия эксперимента можно записать в виде таблицы, где строки соответствуют различным опытам, а столбцы – значениям факторов. Будем называть такие таблицы матрицами планирования эксперимента.
Матрица планирования для двух факторов приведена в табл.17.
Каждый столбец в матрице планирования называют вектор-столбцом, а каждую строку – вектор-строкой. Таким образом, в табл.17 мы имеем два вектора-столбца независимых переменных и один вектор-столбец параметра оптимизации. То, что записано в этой таблице в алгебраической форме, можно изобразить геометрически. Найдем в области определения факторов точку, соответствующую основному уровню, и проведем через нее новые оси координат, параллельные осям натуральных значений факторов. Далее, выберем масштабы по новым осям так, чтобы интервал варьирования для каждого фактора равнялся единице. Тогда условия проведения опытов будут соответствовать вершинам квадрата, центром которого является основной уровень, а каждая сторона параллельна одной из осей координат и равна двум интервалам. Номера вершин квадрата соответствуют номерам опытов в матрице планирования. Площадь, ограниченная квадратом, называется областью эксперимента. Иногда удобнее считать областью эксперимента площадь, ограниченную окружностью, описывающей квадрат.
Таблица 17
| Номер опыта | x1 | x2 | y |
| -1 | -1 | y1 | |
| +1 | -1 | y2 | |
| -1 | +1 | y3 | |
| +1 | +1 | y4 |
Запись матрицы планирования, особенно для многих факторов, громоздка. Для ее сокращения удобно ввести условные буквенные обозначения строк.
Это делается следующим образом. Порядковый номер фактора ставится в соответствие строчной букве латинского алфавита: х1 – а, х2 – b, ... и т. д. Если теперь для строки матрицы планирования выписать латинские буквы только для факторов, находящихся на верхних уровнях, то условия опыта будут заданы однозначно. Опыт со всеми факторами на нижних уровнях условимся обозначать (1). Матрица планирования вместе с принятыми буквенными обозначениями приведена в табл.18.
Таблица 18
| Номер опыта | x1 | x2 | Буквенное обозначение строк | y |
| -1 | -1 | (1) | y1 | |
| +1 | -1 | a | y2 | |
| -1 | +1 | b | y3 | |
| +1 | +1 | ab | y4 |
Если для двух факторов все возможные комбинации уровней легко найти прямым перебором (или просто запомнить), то с ростом числа факторов возникает необходимость в некотором приеме построения матриц. Из многих возможных обычно используется три приема, основанных на переходе от матриц меньшей размерности к матрицам большей размерности. Рассмотрим первый. При добавлении нового фактора каждая комбинация уровней исходного плана встречается дважды: в сочетании с нижним и верхним уровнями нового фактора. Отсюда естественно появляется прием: записать исходный план для одного уровня нового фактора, а затем повторить его для другого уровня. Вот как это выглядит при переходе от эксперимента 22 к 23.(табл.19).
Этот прием распространяется на построение матриц любой размерности.
Рассмотрим второй прием. Для этого введем правило перемножения столбцов матрицы. При построчном перемножении двух столбцов матрицы произведение единиц с одноименными знаками дает +1, ас разноименными –1. Воспользовавшись этим правилом, получим для случая, который мы рассматриваем, вектор-столбец произведения x1 x2 в исходном плане. Далее повторим еще раз исходный план, а у столбца произведений знаки поменяем на обратные.
Этот прием тоже можно перенести на построение матриц любой размерности, однако он сложнее, чем первый.
Таблица 19
| Номер опыта | x1 | x2 | x3 | y |
| - | - | + | y1 | |
| - | + | + | y2 | |
| + | - | + | y3 | |
| + | + | + | y4 | |
| - | - | - | y5 | |
| - | + | - | y6 | |
| + | - | - | y7 | |
| + | + | - | y8 |
Третий прием основан на правиле чередования знаков. В первом столбце знаки меняются поочередно, во втором столбце они чередуются через два, в третьем – через 4, в четвертом – через 8 и т.д. по степеням двойки. Если в табл.5 поменять местами столбцы для x1 и x2, то получится нужная матрица.
По аналогии с полным факторным экспериментом 22 можно дать геометрическую интерпретацию полного факторного эксперимента 23. Геометрической интерпретацией полного факторного эксперимента 23 служит куб, координаты вершин которого задают условия опытов.
Куб задает область эксперимента, а центр куба является ее центром.
К сожалению, мы не умеем рисовать картинки для числа факторов k> 3. Но фигура, задающая область эксперимента в многомерном пространстве, является некоторым аналогом куба. Будем называть эту фигуру гиперкубом.
Геометрическая интерпретация полного факторного эксперимента более подробно будет рассмотрена ниже.
Пример построения 23 линейный план двухуровневый и трехфакторный.
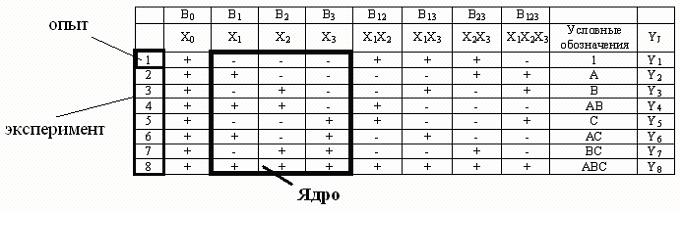
Рис.36. Пример построение ПФЭ 23
Вид каждого плана определяется видом математической модели.
В0 - отражает х0, но в уравнении не пишется, это фиктивный фактор вводится в план для подсчета общего среднего значения.
Все факторы этого плана имеют два уровня измерения, для простоты пишем только + или -.
хiн=-1, хiв=+1.
Ядро плана - это та его часть, по которой осуществляется управление экспериментом, в нем полное сочетание (полный перебор) всех возможных сочетаний для всех факторов и нет никакого повтора. Иногда удобно иметь буквенные обозначения факторов (для операторов).
Для статистической достоверности результатов эксперимента проводятся 3-4 эксперимента.
Каждая строка это условия проведения опыта и его результат. Колонка выходного параметра оценивает эксперимент. Для оценки достоверности результата может производиться повтор только одного опыта.
Регрессионные планы, как правило, строятся для безразмерного обозначения факторов. Безразмерные обозначения позволяют применять другие методы (масштабировать факторы, приводить к одному методу) и центрировать (выбрать другой центр или начало отсчета).

Рис.37. Ось координат размерных величин
Xi меняется от Xiн до Xiв (∆Xi – диапазон)
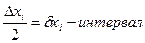
Все значения Xi выбираются из априорного анализа.
Перейдем к Xi – безразмерное обозначение факторов.
Xi0, Xiн, Xiв:
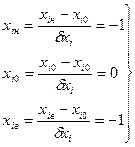 безразмерное обозначение нижнего, среднего и верхнего уровня
безразмерное обозначение нижнего, среднего и верхнего уровня
В математической модели размерность имеют коэффициенты bijk.

Рис.38. Ось координат безразмерных величин
Построение эксперимента с безразмерным обозначением факторов осуществляется по принципу Адамара, и соответствующие планы называются матрицами Адамара.
В плане первым проставляется фактор X0 – фиктивный, записываемый для расчета значений выходного параметра и оценки свойств члена уравнения.
План ПФЭ выражается математической моделью:
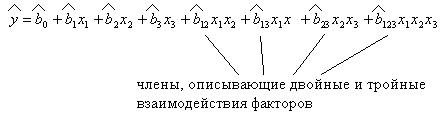
Количеством точек l можно описывать уравнение (l -1) – го порядка.
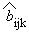 - описывает взаимодействие 3-х факторов (t˚, влажность, P) и это только первый плюс такого плана.
- описывает взаимодействие 3-х факторов (t˚, влажность, P) и это только первый плюс такого плана.
N = g·n,
где N – число опытов, n – число опытов в одном эксперименте, g – число повторных экспериментов.
В связи со сложностью технических систем и с тем, что испытания не всегда могут быть повторены по всем входным параметрам и условиям проведения эксперимента (т.е. в точности эксперимент воспроизвести невозможно), все технические эксперименты являются невоспроизводимыми.
Число g = 3 дает возможность подтверждения результатов эксперимента и рассчитать статистические характеристики.
Рандомизация – опыты должны быть произведены в случайном порядке и отличаться в разных экспериментах.
Свойства планов ПФЭ: ПЭФ 2х2
1. Симметричность (симметричность относительно центра эксперимента) – алгебраическая сумма элементов вектор-столбца каждого фактора равна нулю, или в каждом из столбцов количество факторов на низшем уровне равно количеству факторов на высшем уровне.
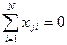 ,
,
где j – номер фактора, N – число опытов, j = 1, 2,…, k.
2. Нормированность (либо условие нормировки) – сумма квадратов элементов каждого столбца равна числу опытов, или 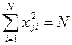 .
.
3. Ортогональность (ортогональность матрицы планирования) – сумма почленных произведений любых двух вектор-столбцов матрицы равна нулю, или 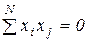
Это говорит о том, что векторы факторов направлены перпендикулярно друг другу и не оказывают существенного влияния друг на друга. Влияние определяется по значению выходного параметра. Приводит к тому, что из уравнения можно выбросить незначительные члены без перерасчета других коэффициентов.

Рис.39. Свойство ортогональности
4. Рототабельность – точки в матрице планирования подбираются так, что точность предсказания значений параметра оптимизации одинакова на равных расстояниях от центра эксперимента и не зависит от направления.
Так же данное свойство говорит о том, что в этом плане получаемые погрешности выходного параметра будут одинаковы на сфере радиуса ρ = 1. Свойство рототабельности позволяет сравнивать значение выходного параметра и количественно определять эффект влияния на него факторов включаемых в модель.
Рис.40. Свойство рототабельности
Yj и Yj+1 – измерены с одной погрешностью.
Это позволит оценить влияние факторов с высокой достоверностью.
При включении факторов в план эксперимента необходимо определить их взаимную коррелированность или техническую совместимость.
Геометрическая интерпретация плана и его математической модели. ПЭФ 2
План эксперимента может быть (в зависимости от числа факторов) представлен различными геометрическими моделями.
а) yj=f(x1) – однофакторная

Рис.41. Интерпретаци однофакторной модели
1 уровень геометрической интерпретации - факторная ось. Однофакторный план ему соответствует уравнение регрессии - однофакторное, линейное, которое интерпретируется линией
б) yj=f(x1,x2) – двухфакторная

Рис.42. Факторная плоскость двухфакторной модели

Рис.43. Геометрическая интерпретация двухфакторной модели
Двухфакторный план - факторная плоскость, в которой работают факторы X1 и Х2. Факторная плоскость ограничена 4 точками ПЭФ. Математическая модель интерпретируется некоторой плоскостью y = j (хi) – плоскость или поверхность отклика или выходного параметра (в случайной линейной зависимости - плоскость, в пространстве - поверхность). Для модели и выше трехфакторной - поверхность отклика - гиперповерхность. Для их исследования их надо разбивать на 2-х факторные условно.
в) yj=f(xi); j=3. – трехфакторная

Рис.44. Факторное пространство трехфакторной модели
Геометрическая интерпретация:
Для модели и выше трехфакторной – поверхность отклика – гиперповерхность. Для их исследования их надо разбивать на 2-х факторные условно.
Таблица 20
| X1 | X2 | X3 | |
| - | - | - | |
| + | - | - | |
| - | + | - | |
| + | + | - | |
| - | - | + | |
| + | - | + | |
| - | + | + | |
| + | + | + |
Поверхность внутри куба - совокупность всех возможных комбинаций трех параметров, вершины - строки плана эксперимента.
Грань куба определяет значение фактора: «+» или «-» единица.
Грани ограничивают факторное пространство состояния факторов. В эксперименте мы работаем на гранях куба (реже внутри куба). За пределами факторного пространства (куба) наша математическая модель работать не будет, не будет давать достоверных результатов. Следовательно, модель работает по интерполяции.
Куб - отражение факторного эксперимента.
Вершина - геометрическая интерпретация одного опыта.
План дробного факторного эксперимента ДФЭ
N=mk-p,
где m - число уровней, p - показатель дробности (p≥1), k - число факторов.
Планы ДФЭ позволяют уменьшить количество опытов в 2 и более раз, но при этом получается накладка влияния факторов и их взаимодействия друг на друга можно определить с помощью специальных действий.
Чтобы сократить число опытов, нужно новому фактору присвоить вектор-столбец матрицы, принадлежащий взаимодействию, которым можно пренебречь. Тогда значение нового фактора в условиях опытов определяется знаками этого столбца.
Пример плана ДФЭ: 24-1
X0 – фиктивный фактор – отсутствует.
N=24-1=8, N=24=16.
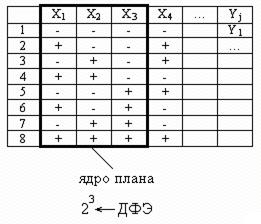
Рис.45. Пример плана ДФЭ 24-1
1) Планирование дополнительного столбца выполняется с помощью планирующих соотношений.
ПС: x4=x1x2x3
Выбирается такое планирующее соотношение, которое дает минимальный эффект на выходной параметр.
2) Записываются определяющие соотношения.
ОС: x4x4=x1x2x3 x4
1 = x1x2x3 x4
3) Построение эффектов смешения для каждого члена математической модели (т.е. умножаем обе части уравнения, определяющего соотношения, на соответствующий член).
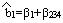
β1 – истинный эффект от воздействия x1
1·x1= x1x1x2x3 x4
x1x1 = 1
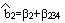
Таким образом, построив смешивающие эффекты, можно узнать какой из факторов имеет наибольшую погрешность в отображении математической модели, полученной по дробному факторному эксперименту.

Рис.46. Смещение истиной оценки
Пример плана ДФЭ: 25-2
N=25-2, 2- говорит о том, сколько факторов из ядра плана заменяется на взаимодействие и одновременно показывает насколько сокращается число опытов.
N=25-2=8, N=25=32.
Таблица 21
| X1 | X2 | X3 | X4 | X5 | X1X2 | … | Yj | |
| - | - | - | + | - | + | |||
| + | - | - | + | + | - | |||
| - | + | - | - | + | - | |||
| + | + | - | - | - | + | |||
| - | - | + | - | + | + | |||
| + | - | + | - | + | - | |||
| - | + | + | + | - | - | |||
| + | + | + | + | + | + |
Алгоритм плана ДФЭ:
1. В соответствии с показателем q выбираются планирующие соотношения
x4 = x2x3
x5 = x1x2x3
Планирующие соотношения:
1. В ДФП замещаемые факторы планируются как взаимодействия, при этом выбираются наиболее слабые взаимодействия, 3 или более из парных выбираем из таблицы взаимодействий.
2. Описание планирующего соотношения, планирующее соотношение расписывается для факторов, являются дополнительным к ядру плана ДФЭ.
Ядро ДФЭ включает в себя количество факторов ядра k-p, т.е. 5-2=3, т.е. в ядре 3 фактора.
3. Построение ПЭФ для факторов ядра.
4. Строим планирующие соотношения для дополнительных факторов.
5. Запись определяющего соотношения, ОС строится для оценки эффектов смешивания факторов и взаимодействий, они выявляются для каждого элемента математической модели для ДФЭ (оценивается наложение искажающих эффектов):
Обе части ПС умножаются на левую часть
x4x4 = x2x3 x4
x5x5 = x1x2x3 x5
x4x4 = 1 → 1 = x2x3 x4
x5x5 = 1 → 1 = x1x2x3 x5
ГОС (генеральное определяющее соотношение) получается в результате перемножения.
ГОС: 1=x2x3x4=x1x2x3x5=x1x4x5 говорит о том, что каждый из факторов будет иметь 3 составляющих погрешности.
6. Введем bi- истинное значение коэффициента регрессионной модели.
7. Определение эффекта смешивания
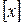 - оценочное значение коэффициентов относительно него.
- оценочное значение коэффициентов относительно него.
Составляющие погрешности – B1, В2,В3, …
Эффекты двойные и одинарные, как правило, имеют один количественный уровень, поэтому необходимо избегать смешивающих эффектов и применять ДФЭ только для k>4 (смешивание эффектов больше 3 порядка оказывает min смещение на оценке основных коэффициентов). Смешивание воздействий вызывает смещение оценок от истинного значения. ГОС умножаем на x1:
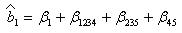
x1=x1x2x3x4=x1x1x2x3x5=x1x1x4x5
Говорит о том, что при получении значений регрессионного уравнения вi на значении коэффициента на в1, например, оказывают воздействие так называемые смешивающие коэффициенты b123, b235, b45 они вызывают смещение значения Bi относительно истинного. Таким образом, с помощью ОС можно оценить влияние эффектов смешивания.
Для многих технических экспериментов применение ПФЭ оправданно, в связи с тем, что возможно выбрать слабые эффекты взаимодействия и снизить влияние смешивающих эффектов, либо выбор планирующего соотношения из взаимодействий более высокого порядка. Можно снизить дробность плана.
Планы 2-го порядка
1. ОЦКП - ортогональный центральный композиционный план;
2. РЦКП - рототабельный центральный композиционный план;
3. BK - планы Бокса;
Планы второго порядка имеют количество уровней больше 2, как правило, композиционные (т.е. линейные и нелинейные части), и могут использоваться в основе как ядро планы ПФЭ и ДФЭ.
Ортогональный центральный композиционный план ОЦКП.
Ядро ОЦКП – дробный факторный эксперимент
Число опытов ОЦКП – Nоцкп= m k-p +2к+kо,
где m k-p – ядро, 2к - квадратичная часть, kо - центральная часть (для ОЦКП всегда равно «1»)
ОЦКП 2 3-1
N= 2 2-1+2·3+1=11
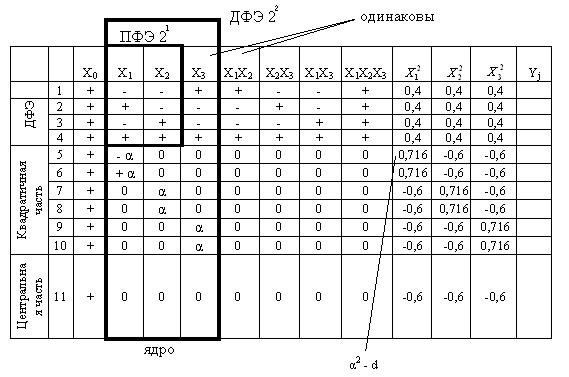
Рис.47. Пример плана ОЦКП 23-1
 Рис.48. Ось координат для ОЦКП
Рис.48. Ось координат для ОЦКП
±a - «звездное плечо» или дополнительный уровень плана ОЦКП - значение фактора, превышающее верхний или нижний уровень; его значение вычисляется исходя из ортогональности плана.
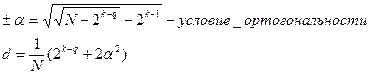 ,
,
где d - квадратичная поправка.
В нашем примере: d=0,6, a=l,147, ki=3.
Условие выполнения в формуле a определяется необходимостью соблюдения ортогональности всех векторов коэффициентов регрессионного уравнения.
α и d позволяют осуществить принцип ортогональности (независимости) всех столбцов матрицы и соответственно всех членов уравнения относительно друг друга.
ОЦКП позволяет построить математическую модель от 2-го до 4-го порядка.
Особенности плана ОЦКП:
1. Модель, полученная использованием ОЦКП имеет взаимно независимые коэффициенты, так, что статистически незначимые из них можно исключить из уравнения без пересчета остальных коэффициентов. Это определяется свойством ортогональности плана.
2. План позволяет построить сначала линейную модель и провести только часть опытов для линейной части плана. В том случае если уравнение будет неадекватно экспериментальным данным, т.е. оно будет иметь порядок выше первого, соответственно этой проверке, эксперимент можно провести по квадратичной части плана и получить нелинейную модель. Такой поэтапный алгоритм эксперимента позволяет выявить линейную модель на первом этапе эксперимента и соответственно сократить количество опытов. Это определяется композиционностью плана.
Рототабельньй центральный композиционный план РЦКП.
В основе построения этих планов лежит свойство рототабельности.
Рототабельность - это свойство дисперсии выходного параметра, при котором погрешность yi на одинаковом расстоянии от центра эксперимента будет одинаковой (дисперсия в этом случае одинакова на поверхности шара). Это один из объективных факторов при оценке эффективности факторов при их сравнении.
Рототабельный план: строится аналогичный ОЦКП, состоит из трех частей: линейной, квадратичной и осевой.
План построения плечей выбирается из условий рототабельности.
Таблица 22
| k | ядро | Количество точек в центре | α | Общее N опытов |
| 22 | 1,414 | |||
| 23 | 1,680 | |||
| 24 | 2,000 | |||
| 25 | 2,378 | |||
| 25-1 | 2,000 | |||
| 26 | 2,828 | |||
| 26-1 | 2,378 | |||
| 27 | 3,333 | |||
| 27-1 | 2,828 |
k – количество точек в центральной части плана. У РЦКП k ≠ 1 в отличие от ОЦКП.
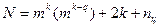
ρ=a (сфера с радиусом ρ)
Такие планы позволяют получить одинаковую дисперсию выходного параметра:
на поверхности шара 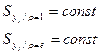
R = ρ = 1 – униформпланы
либо ρ = const, но в пределах ±α.

Рис.49. Факторная область для планов ОЦКП
Условие рототабельности:
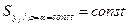
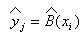
План Бокса (Вк)
Применяются при оценочных экспериментах, является почти ортогональным (т.е. коэффициенты почти независимые).
План Бокса является композиционным и состоят из двух частей, не имеет центральной части.
Bk: В3-1 - трехфакторный план Бокса (2 3-1).
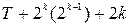
Таблица 23
| X1 | X2 | X3 | ||
| Ядро 23-1 | - | - | + | |
| + | - | - | ||
| - | + | - | ||
| + | + | + | ||
| Квадратичная часть | - | |||
| + | ||||
| - | ||||
| + | ||||
| - | ||||
| + |
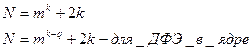
В плане Бокса вместо «звездных» плечей записывают верхний (+) и нижний (—) уровни фактора. План позволяет получить математическую модель второго порядка, но с меньшей точностью, чем ОЦКП и РКЦП. Используется для предварительной оценки. Этот план является почти рототабельным.
План Бокса - Бенкена (В-В)
В-В: k=4.
Общая структура плана:
Таблица 24
| X0 | X1 | X2 | X3 | X4 | |
| a | a1 | a2 | 0 | 0 | |
| a | a1 | 0 | a2 | 0 | |
| a | 0 | a1 | a2 | 0 | |
| a | a1 | 0 | 0 | a2 | |
| a | 0 | a1 | 0 | a2 | |
| a | 0 | 0 | a1 | a2 |
аi- матрицы из четырех опытов.
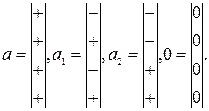
Таблица для расчета плана Блока - Бенкена:
Таблица 25
| k | k0 | N |
План позволяет получить высокую точность математической модели, обладающей высокой рототабельностью и ортогональностью. Для этого плана не нужно рассчитывать рототабельность и ортогональность. Недостатком является отсутствие композиционности.
План Рехтшафнера
План Рехтшафнера имеет частичную выборку из плана 3. Этот план почти композиционный, не симметричный. При расчете может быть использован метод наименьших квадратов.
Структура плана:
Таблица 26
| № | a | b | c | Число точек | Код | |
| X0 | X1 | X2 | X3 | |||
| + | - | - | - | (1) | ||
| + | - | + | + | n=3 | bc | |
| + | + | - | + | ac | ||
| + | + | + | - | ab | ||
| + | + | n=3 | a(0) | |||
| + | + | b(0) | ||||
| + | + | c(0) | ||||
| + | - | - | + | n(n-1)/2 =3 | c | |
| + | - | + | - | b | ||
| + | + | - | - | a |
Полученная математическая модель второго порядка является рототабельной и ортогональной.
Технологические рекомендации по результатам планирования
1. Использование линейных и нелинейных планов. Определение по априорным данным (они устанавливают наличие нелинейности в исследуемых объектах).
2. Проведение эксперимента должно сопровождаться не менее чем трехкратным повторением опытов и использованием принципов рандомизации по каждому эксперименту в целях получения более достоверных результатов.
3. Использование планов должно сопровождаться контролем четырех основных свойств: симметричности, нормированности, ортогональности и рототабельности.
4. При проведении эксперимента необходимо обеспечить запись каждого опыта и соответствующих условий. При установлении основных отклонений при повторе целесообразно провести новый опыт или замер. Достоверность экспериментальных данных возможна при условии соблюдения данных, которые были установлены для блока технологического оснащения.
Дата добавления: 2016-11-02; просмотров: 3211;
