Алгоритм вторичной обработки экспериментальных данных
Входными условиями для этапа вторичной обработки экспериментальных данных по МНК являются: |x|, |y|, N(•) по каждому опыту матрицы Y.
1) Определение коэффициентов регрессионного уравнения:
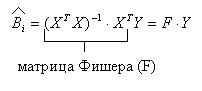
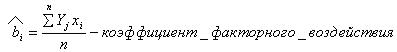
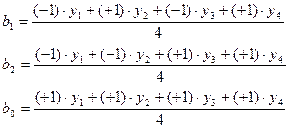
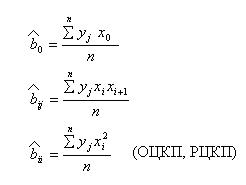
Пример:
Таблица 27
| X1 | X2 | X1X2 | Yср | |
| - | - | + | ||
| + | - | - | ||
| - | + | - | ||
| + | + | + | ||
| b1 | b2 | b12 |
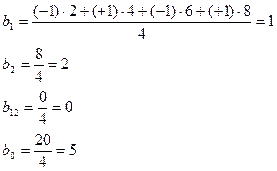
b0 = 5, так как x0 → все «+»
Математическая модель:
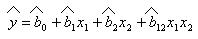
Ответ:
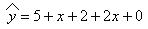
2) Определение остаточной дисперсии (S2остаточн.), или дисперсии адекватности(S2ад.):
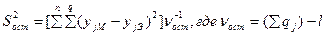
либо
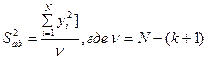
q, N – количество замеров в первом опыте
l, k – количество коэффициентов регрессионного уравнения
Пример
Провели полный факторный эксперимент 23.
Число степеней свободы будет
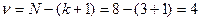
3) Определение дисперсии коэффициентов регрессионного уравнения
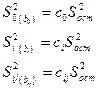
4) Проверка значимости коэффициентов
Можно осуществлять двумя способами: проверкой по t-критерию Стьюдента или построением доверительного интервала. При использовании полного факторного эксперимента доверительные интервалы (в том числе и эффектов взаимодействия) равны друг другу.
Прежде всего надо найти дисперсию коэффициента регрессии 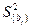 . Она определяется по формуле
. Она определяется по формуле
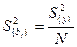 , если параллельные опыты отсутствуют.
, если параллельные опыты отсутствуют.
Из формулы видно, что дисперсии всех коэффициентов равны друг другу, так как они зависят от ошибки опыта и числа опытов.
Теперь построим доверительный интервал ( Δbj )
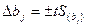
Здесь t – табличное значение критерия Стьюдента при числе степеней свободы, с которыми определялась 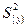 , и выбранном уровне значимости (обычно 0,05);
, и выбранном уровне значимости (обычно 0,05); 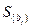 - квадратичная ошибка коэффициента регрессии
- квадратичная ошибка коэффициента регрессии
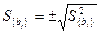
Формулу для доверительного интервала можно записать в следующей эквивалентной форме:
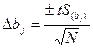
Коэффициент значим, если его абсолютная величина больше доверительного интервала. Доверительный интервал задается верхней и нижней границами 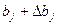 и
и 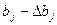 .
.
Для отыскания значения t–критерия можно воспользоваться таблицей, фрагмент из которой преведен в табл. 60.4.
Таблица построена следующим образом. Столбцы соответствуют различным степеням свободы и значениям критерия.
Пусть в двух различных случайно оказались два численно равных коэффициента регрессии. Доверительные интервалы для них оказались различными. Из них значим только второй
Таблица 28
| Задача | 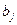
| 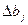
|
| 5,3 | ±5,5 | |
| 5,3 | ±2,6 |
Таблица 29
| Число степеней свободы | Значения t–критерия | Число степеней свободы | Значения t–критерия | Число степеней свободы | Значения t–критерия |
| 12,71 | 2,201 | 2,080 | |||
| 4,303 | 2,179 | 2,074 | |||
| 3,182 | 2,160 | 2,069 | |||
| 2,776 | 2,145 | 2,064 | |||
| 2,571 | 2,131 | 2,060 | |||
| 2,447 | 2,120 | 2,056 | |||
| 2,365 | 2,110 | 2,052 | |||
| 2,306 | 2,101 | 2,048 | |||
| 2,262 | 2,093 | 2,045 | |||
| 2,228 | 2,086 | 2,042 | |||
| ∞ | 1,960 |
В действительности чем уже доверительный интервал (при заданном α), тем с большей уверенностью можно говорить о значимости коэффициента.
Рабочее правило: если абсолютная величина коэффициента больше, чем доверительный интервал, то коэффициент значим. Если больше нравится проверять значимость коэффициента по t–критерию, то воспользуйтесь формулой
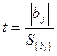
Вычисленное значение t–критерия сравнивается с табличным при при заданном α и соответствующем числе степеней свободы. Полученные выводы о значимости коэффициентов должны совпадать с предыдущими.
Так производится проверка значимости коэффициентов.
Н0:
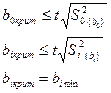
Н0 (гипотеза): Если значение коэффициента регрессионного уравнения удовлетворяет неравенству, то коэффициент регрессии считается статически незначимым на заданном уравнении вероятности и может быть изъят из уравнения регрессии.
Для математической модели, полученной по ортогональным планам, при выбросе незначимых коэффициентов остальные не пересчитываются.
5) Оценка адекватности регрессионной модели:
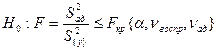
Yср. по плану – среднее значение выходного параметра по строкам и столбцам (т.е. со всеми повторами).
Если гипотеза удовлетворяется, то считается, что регрессионное уравнение адекватно, т.е. соответствует экспериментальным значениям и описывает функцию y = f(x) достаточно достоверно на заданном уровне вероятности p.
Дата добавления: 2016-11-02; просмотров: 1581;
