Пример построения диаграммы

Априорный анализ

- описание объекта,

- описание воздействия (фактора) X_i,

- определение числа Х_i, i == 5,

- определение Х_iн, X_iо, Х_iв, ..., D Xi, D X₂.

N_{повторов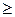} 3

Рис.25. Диаграмма рассеивания

q_н - число точек, которое считается для нижнего уровня по количеству точек ниже нижней точки на верхнем уровне, для верхнего уровня – количестве точек выше верхней точки на нижнем уровне (q_в). q = q_н + q_в, m_i – медиана, средняя точка на каждом уровне фактора, 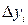- разница медиан, .

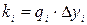q₁=3+3=6, Dy₁=5, k₁= 30

q₂=1, Dy₂=3, k₂=3

q₃=-6, Dy₃=4, k₃=-24

q₄=0, Dy₄=O, k₄=0

q₅=2+2=4, Dу₅=5, k₅=20

X₁, Х₂, X₅ - существенные факторы, X₃ - малосущественный, X₄ -несущественный. Существенные и малосущественные факторы заносятся либо в математическую модель, либо в техническое задание на проект стенда.

Основные термины планирования эксперимента

Случайная величина x_i (i = 0, l, 2, 3,..., k) - входное воздействие, факторы, условия внешней среды.

Y_j (j = 1,2,..., n) - выходной параметр или отклик на внешнее воздействие отражает поведение объекта или является характеристикой процесса.

Статистическая связь - устанавливается между x_i и y_j если каждому значению независимой величины х_i соответствует сопряженное значение y_j последнее значение связывается статистическими параметрами с о и т. 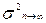среднее квадратичное отклонение, теоретическая дисперсия S(y_j-y_cp)²/n-l или S²_n³3…¥ эмпирическая дисперсия.

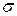устанавливается для генеральной совокупности экспериментальных данных n®¥.

M{y_j} - теоретическое значение выходного параметра в точках экспериментов при n®¥.

y_сp, y_j y_j - среднее для всего эксперимента

Корреляционная связь - статистическая связь между у и х определяется по значениям коэффициентов корреляции г,р-0...1.