Корреляционное отношение можно рассчитать и по такой формуле
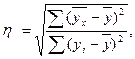 ( 8 )
( 8 )
где 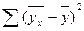 - сумма квадратов отклонений групповых средних
- сумма квадратов отклонений групповых средних 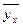 от общей средней
от общей средней 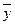 .
.
Значения h распределены на отрезке[0; 1]: 0 £ h £ 1. Чем ближе h к 1, тем теснее связь между переменными Х и Y, тем больше колеблемость Y объясняется колеблемостью X.
В случае линейной зависимости r = h. Если связь — нелинейная, то r < h. Это позволяет использовать h в качестве меры линейности связи между переменными Х и Y. Если коэффициент корреляции r мало отличается от корреляционного отношения h, то зависимость между переменными близка к линейной. В противном случае имеет место нелинейная зависимость между Х и Y.
Проверка значимости корреляционного отношения осуществляется с помощью критерия Фишера (F). Его значение рассчитывается по формуле:
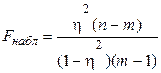 , ( 9 )
, ( 9 )
где п — объем выборки; т — число групп.
Число групп, по которым осуществляется группировка исходных данных, можно определить по формуле Стерджесса:
m =1+3,322· lgN. (10 )
Критическое значение F определяется по таблицам распределения Фишера (приложение ) по уровню значимости а и числу степеней свободы: Fтеор.(a;n1;n2), где n1 = m - 1; n2 = n - m;
Уровень значимости — это достаточно малое значение вероятности, отвечающее событиям, которые в данных условиях исследования будут считаться практически невозможными. Появление такого события считается указанием на неправильность начального предположения. Чаще всего пользуются уровнями a= 0,05 или a = 0,01.
Расчетное значение Fнабл необходимо сравнить с теоретическим Fтеор. По общему правилу проверки статистических гипотез:
- если Fнабл< Fкр, нулевую гипотезу о том, что h незначим, нельзя отклонить;
- если Fнабл ³Fкр, нулевая гипотеза отклоняется в пользу альтернативной. Коэффициент hзначимо отличается от нуля.
Квадрат эмпирического корреляционного отношения (h2) называют коэффициентом детерминации. Он показывает, какая часть колеблемости Y объясняется колеблемостью X.
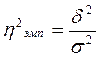 .
.
Он характеризует роль факторной вариации в общей вариации и может быть исчислен как с помощью дисперсионного анализа (разложением дисперсий методом аналитических группировок), так и с помощью регрессионных уравнений.
1.8. Оценка линейности взаимосвязи
Для оценки степени приближения нелинейной зависимости к линейной используется критерий F:
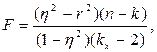
где h2 – квадрат корреляционного отношения; r2 – квадрат коэффициента корреляции; n – объем выборки; kX – число групп по ряду X.
Теоретические значения Fтеор находятся по заданному уровню значимости a и числу степеней свободы n1 = kX и n2 = n - 2.
Если Fрасч < Fтеор – связь практически можно считать линейной.
Если Fрасч. ³ Fтеор. – корреляция нелинейная.
Рассмотрим проверку гипотезы линейности на основе данных предыдущего примера.
Значение коэффициента корреляции равно r = - 0,808.
Расчетное значение критерия F по формуле :

Теоретическое значение критерия F для числа степеней свободы n1 = 10 и n2 = 37 равно Fтеор = 2,18. Видно, что Fрасч < Fтеор. Таким образом, можно считать, что связь между рассматриваемыми факторами практически линейная.
1.9. Ранговая корреляция
Если п объектов какой-либо совокупности N пронумерованы в соответствии с возрастанием или убыванием какого-либо признака X, то говорят, что объекты ранжированы по этому признаку. Ранг х. указывает место, которое занимает i-й объект среди других п объектов, расположенных в соответствии с признаком Х (1= 1,2,..., п). Например, при исследовании рынка мы можем задать вопрос с целью выяснения предпочтений потребителей при выборе товара (при покупке акций, мороженого, водки и т. п.) таким образом, чтобы они распределили товар в порядке возрастания (или убывания) своих потребительских предпочтений. Если мы имеем 2 набора ранжированных данных, то можно попытаться установить степень линейной зависимости между ними. Предположим, имеется 5 продуктов, расположенных по порядку предпочтений от 1 до 5 в соответствии с двумя характеристиками А и В (табл.1.4).
Таблица 1.4
| Характеристики для ранжирования | Продукт | ||||
| V | W | X | У | Z | |
| А В |
Для определения наличия взаимосвязи между ранговыми оценками используется коэффициент ранговой корреляции Спирмена. ,Его расчет основан на различии между рангами:
D = Ранг А - Ранг В.
Коэффициент корреляции рангов Спирмена р рассчитывается по формуле:
где п - число пар ранжированных наблюдений.
В нашем примере мы имеем 5 пар рангов, следовательно, л = 5.
т. е. между признаками есть достаточно сильная линейная связь. Этот коэффициент изменяется в промежутке от [-1; 1] и интерпретируется так же, как и коэффициент Пирсона. Разница лишь в том, что он применяется для ранжированных данных.
Значимость коэффициента Спирмена проверяется на основе (t-критерия Стьюдента по формуле
Значение коэффициента считается существенным, если tнабл > tкрит (a; k=n- 2).
Дата добавления: 2016-10-17; просмотров: 1290;
