Оценка достоверности коэффициента корреляции

Коэффициент парной корреляции, рассчитанный по выборочным данным, является случайной величиной. С уменьшением числа наблюдений надежность коэффициента корреляции падает. С увеличением числа наблюдений (свыше 500) распределение коэффициента корреляции r (не превышающее 0,9) стремится к нормальному.

Определенный по выборке коэффициент корреляции г является оценкой коэффициента корреляции r генеральной совокупности.

Доверительный интервал для оценки истинного значения коэффициента корреляции в генеральной совокупности (r) имеет вид:

r – t_табл s_r £ r £ r + t_табл s_r, ( 5 )

где s_r — средняя квадратическая ошибка выборочного коэффициента парной корреляции; t_табл — параметр распределения Стьюдента с числом степеней свободы k = п - 2 и уровнем значимости а.

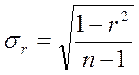
Если коэффициент корреляции меньше 0,9 или выборка мала, среднеквадратическая ошибка выборочного коэффициента корреляцииs_r рассчитывается по формуле

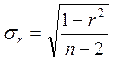
Значимость коэффициента корреляции можно проверить с помощью статистики t, распределения Стьюдента с n - 2 степенями свободы.

Наблюдаемое значение t (t_набл) вычисляется как

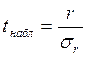
Критическое значение (t_табл) определяется по таблице распределения Стьюдента (приложение ) по уровню значимости а и числу степеней свободы k=п-2.

По общему правилу проверки статистических гипотез:

— если t_набл < t_табл, принимается нулевая гипотеза Н₀: r = 0 т.е. между Х и Y отсутствует корреляционная связь (при заданном уровне значимости);

— если t_набл ³ t_табл, принимается альтернативная гипотеза Н₁: r ¹ 0, т.е. коэффициент корреляции значимо отличается от нуля и можно говорить о наличии корреляционной зависимости между Yи Х.

Критерий t подчиняется закону распределения Стьюдента с п - 2 степенями свободы.

Для оценки значимости r при малом объеме выборки целесообразно использовать z-преобразование Фишера. Для этого применяется статистика z:

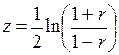, (6)

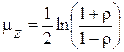
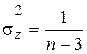Распределение z асимптотически приближается к нормальному. Вариация z выражается формулой, которая распределена по нормальному закону со средним m_z и дисперсией s_z²:

Область принятия гипотезы о нулевой корреляции имеет вид:

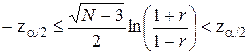, (7)

где z – стандартная, нормально распределенная случайная величина. Если расчетное значение окажется вне этого интервала, то это будет признаком наличия статистической корреляции с уровнем значимости a.

Для a = 0,05 z_a/2 = 1,96; a = 0,02 z_a/2 = 2,32;

a = 0,01 z_a/2 = 2,58; a = 0,1 z_a/2 = 1,64.

Пример 1. Менеджера туристической ком­пании интересует, насколько возрастает привлека­тельность гостиницы в зависимости от ее расстоя­ния до пляжа. С этой целью по 14 гостиницам горо­да была выяснена среднегодовая наполняемость но­меров и расстояние в километрах от пляжа. Статистические данные приведены в таблице 2

Таблица 2 - Данные к примеру 1

На рисунке видно, что связь между исследуемыми факторами обратно пропорциональная, т. е. с увеличением расстояния гостиницы от пляжа ее наполняемость ее уменьшается.

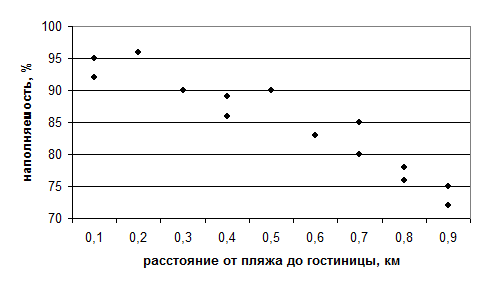
Рисунок 4 – Поле корреляции для примера 1

Оценим силу связи между исследуемыми факторами с помощью коэф-фициента корреляции. Значение коэффициента корреляции r = 0,94 говорит о наличии достаточно сильной обратно пропорциональной зависимости между данными факторами. Так как выборка мала (n < 30), то целесообразно произвести проверку значимости коэффициента корреляции с помощью z-преоб-разования Фишера. Расчеты показали, что z_расч.=5,87 > z _табл.= 1,96 при уровне значимости a=0,05. Таким образом, нет оснований, сомневаться в присутствии связи между исследуемыми факторами.