Частная линейная корреляция
Частный коэффициент корреляции - это показатель, измеряющий степень сопряженности двух признаков.
Математическая статистика позволяет установить корреляцию между двумя признаками при постоянном значении третьего, не ставя специального эксперимента, а используя парные коэффициенты корреляции r12, r13, r23.
Частные коэффициенты корреляции рассчитывают по формулам:
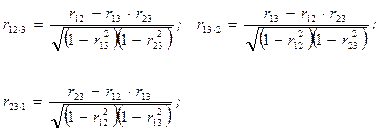
Цифры перед точкой указывают, между какими признаками изучается зависимость, а цифра после точки - влияние какого признака исключается (элиминируется). Ошибку и критерий значимости частной корреляции определяют по тем же формулам, что и парной корреляции:
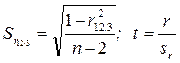 .
.
Теоретическое значение t-критерия определяется для v = n – 2 степеней свободы и принятого уровня значимости a (приложение 1).
Нулевая гипотеза о равенстве частного коэффициента корреляции в совокупности нулю (Ho: r = 0)принимается, если tф < tт, и отвергается, если
tф ³ tт.
Частные коэффициенты могут принимать значения, заключенные между -1 и+1. Частные коэффициенты детерминации находят путем возведения в квадрат частных коэффициентов корреляции:
D12.3 = r212ּ3; d13.2 = r213ּ2; d23ּ1 = r223ּ1.
Определение степени частного воздействия отдельных факторов на результативный признак при исключении (элиминировании) связи его с другими признаками, искажающими эту корреляцию, часто представляет большой интерес. Иногда бывает, что при постоянном значении элиминируемого признака нельзя подметить его статистического влияния на изменчивость других признаков. Чтобы уяснить технику расчета частного коэффициента корреляции, рассмотрим пример. Имеются три параметра X, Y и Z. Для объема выборки n = 180 определены парные коэффициенты корреляции
rxy = 0,799; rxz = 0,57; ryz = 0,507.
Определим частные коэффициенты корреляции:
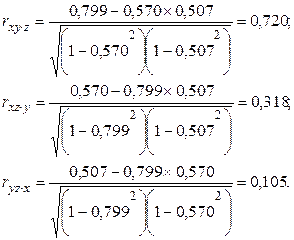
Частный коэффициент корреляции между параметром X и Y с постоянным значением параметра Z (rхуּz = 0,720) показывает, что лишь незначительная часть взаимосвязи этих признаков в общей корреляции (rxy = 0,799) обусловлена влиянием третьего признака (Z). Аналогичное заключение необходимо сделать и в отношении частного коэффициента корреляции между параметром X и параметром Z с постоянным значением параметраY (rхzּу = 0,318 и rxz = 0,57). Напротив, частный коэффициент корреляции между параметрами Y и Z с постоянным значением параметра X ryzּx = 0,105 значительно отличается от общего коэффициента корреляции rуz = 0,507. Из этого видно, что если подобрать объекты с одинаковым значением параметра X, то связь между признаками Y и Z у них будет очень слабой, так как значительная часть в этой взаимосвязи обусловлена варьированием параметра X.
При некоторых обстоятельствах частный коэффициент корреляции может оказаться противоположным по знаку парному.
Например, при изучении взаимосвязи между признаками X, У и Z - были получены парные коэффициенты корреляции (при n = 100): rху = 0,6; rхz= 0,9;
rуz = 0,4.
Частные коэффициенты корреляции при исключении влияния третьего признака:
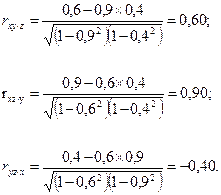
Дата добавления: 2016-10-17; просмотров: 649;
