Недетерминированный алгоритм решения множества уравнений

Вход: множество уравнений .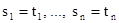

Выход: множество уравнений в разрешённой форме .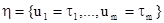

Действия: пока истинно условие применимости хотя бы одного из перечисленных далее преобразований, выполнять в цикле альтернативы.

Начало цикла:

I. если существует уравнение вида: t = x, где t – не переменная, а x – переменная, то заменить это уравнение на x = t; в противном случае

II. если существует уравнение вида: x = x, где x – переменная, то удалить это уравнение из системы уравнений; в противном случае

III. если существует уравнение вида: s = t, в котором s и t не являются переменными, то если корневые функции термов s и t различны, тогда возвращается «отказ», в противном случае осуществить преобразование редукции термов;

IV. если существует уравнение вида: x = t, такое, что переменная x не входит в другие уравнения системы и терм t отличен от x, то если переменная x входит в t, тогда возвращается «отказ», в противном случае осуществить преобразование элиминации переменной.

Конец цикла. (Возвращается «успех», преобразованная система уравнений будет искомым унификатором.)

Здесь под элиминацией переменной понимается переход от системы уравнений к системе, полученной после подстановки x = t.

Пример

Рассмотрим систему, состоящую из одного уравнения:

((a Ç b) È d) È (a Ç b) = (c È (a Ç b) È (a Ç b)}

1) Применяем случай III, делаем редукцию, получаем: h = {(a Ç b) È d) = c È (a Ç b), a Ç b = a Ç b}.

2) Применяем случай III, получаем: h = {a Ç b = с, d = a Ç b, a Ç b = a Ç b}.

3) Применяем случай III для последнего уравнения и повторяем 2 раза случай II, это приводит к h = {a Ç b = с, d = a Ç b}.

4) Применяем случай I, получаем ответ: h = {c = a Ç b, d = a Ç b}.