Предикаты и отношения
Функция n переменных, принимающая значения 0 и 1, называется n-местным предикатом. Каждому отношению 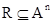 соответствует предикат, равный характеристической функции подмножества R. Ясно, что определение n-местного предиката
соответствует предикат, равный характеристической функции подмножества R. Ясно, что определение n-местного предиката 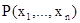 на множестве А равносильно заданию отношения:
на множестве А равносильно заданию отношения:
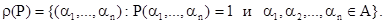
Пусть 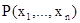 и
и 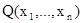 – предикаты. Конъюнкцией P и Q называется предикат
– предикаты. Конъюнкцией P и Q называется предикат 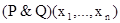
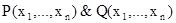 , дизъюнкцией – предикат
, дизъюнкцией – предикат 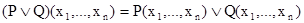 , отрицание определяется с помощью предиката
, отрицание определяется с помощью предиката 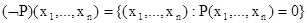 .
.
Для предикатов определяются кванторы существования и всеобщности. Пусть 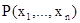 – n-местный предикат. Запись:
– n-местный предикат. Запись: 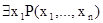 означает, что существует
означает, что существует 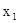 , для которого
, для которого 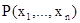 =1, запись:
=1, запись: 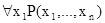 означает, что
означает, что 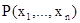 =1 для всех
=1 для всех 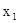 . Аналогично определяются предикаты
. Аналогично определяются предикаты 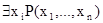 и
и 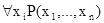 , при
, при 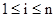 . В этих случая говорят, что переменная
. В этих случая говорят, что переменная 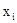 связана квантором. Предикаты
связана квантором. Предикаты 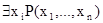 и
и 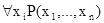 будут зависеть от n-1 переменных. В случае, когда
будут зависеть от n-1 переменных. В случае, когда 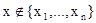 , положим
, положим 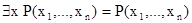 и
и 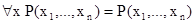 . Тем самым мы определим предикаты
. Тем самым мы определим предикаты 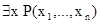 и
и 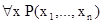 для любых символов переменных x. Отношение, соответствующее предикату
для любых символов переменных x. Отношение, соответствующее предикату 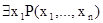 будет проекцией отношения, определяемого P, на область
будет проекцией отношения, определяемого P, на область 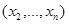 , оно будет равно объединению по всем aÎA отношений, определяемых предикатами
, оно будет равно объединению по всем aÎA отношений, определяемых предикатами 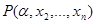 . Предикату
. Предикату 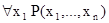 соответствует отношение, равное пересечению этих отношений. Таким образом,
соответствует отношение, равное пересечению этих отношений. Таким образом,
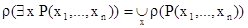 ;
;
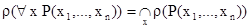 .
.
Дата добавления: 2016-09-20; просмотров: 860;
