Язык логики предикатов
Определим синтаксис языка первого порядка. Алфавит языка первого порядка состоит из логических символов Ú, Ø, $, =, из символов переменных 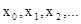 и из нелогических символов. К логическим символам отнесём символы скобок и запятой. В качестве символов переменных будем использовать также x, y, z, u, v и т.д. Логические символы одинаковы для всех языков первого порядка. Нелогическими называются символы операций, символы предикатов и символы констант. Язык первого порядка L задаётся как множество нелогических символов. Если L = Æ, то L называется языком чистого равенства.
и из нелогических символов. К логическим символам отнесём символы скобок и запятой. В качестве символов переменных будем использовать также x, y, z, u, v и т.д. Логические символы одинаковы для всех языков первого порядка. Нелогическими называются символы операций, символы предикатов и символы констант. Язык первого порядка L задаётся как множество нелогических символов. Если L = Æ, то L называется языком чистого равенства.
Каждому s Î L ставится в соответствие #(s) Î w. Если s – константа, то #(s) = 0. Если R – символ предиката, такого, что #(R) = n, то R называется символом n-местного предиката. Если f – символ операции, и #(f) = n, то f называется символом n-арной операции. Для предикатов и операций число #(R) (соответственно #(f)) больше 0, и оно называется местностью (соответственно арностью). Объединение множеств символов операций и констант составляет множество функциональных символов, позволяющее строить термы языка L на множестве 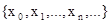 .
.
К предикатам языка L мы всегда относим бинарный предикат 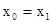 (равенство). Определим формулы языка L.
(равенство). Определим формулы языка L.
Атомной формулой языка L называется выражение вида: 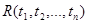 , где
, где 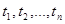 – термы языка L, а R Î L – символ n-местного предиката. В частности, выражение
– термы языка L, а R Î L – символ n-местного предиката. В частности, выражение 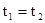 будет атомарной формулой для любых термов языка L. Множество всех формул языка L определяется как наименьшее множество выражений, которое содержит все атомные формулы и удовлетворяет условиям: если q и y – формулы, а x – переменная, то выражения
будет атомарной формулой для любых термов языка L. Множество всех формул языка L определяется как наименьшее множество выражений, которое содержит все атомные формулы и удовлетворяет условиям: если q и y – формулы, а x – переменная, то выражения 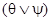 , Øq, $xq – формулы. Формулы q и y называются подформулами формулы
, Øq, $xq – формулы. Формулы q и y называются подформулами формулы 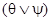 , формула q – подформулой формул Øq и $xq.
, формула q – подформулой формул Øq и $xq.
Будем предполагать, что другие логические связки служат сокращениям:
(q & y) для Ø(Øq Ú Øy),
(q ® y) для (Øq Ú y),
" x q для Ø$ x Øq.
Формула Øx = y обычно записывается как x ¹ y. Примеры формул:
" x $ y P (x, y, x È z), $ x (y £ x ® y = x).
Замена переменных
Переменная, содержащаяся в формуле, называется свободной, если она не связана квантором, в противном случае она называется связанной. Переменная может входить в формулу несколько раз, в этом случае аналогичные определения применяются к каждому вхождению. Например, в формуле
" y (y = z) ® $ z (z < x)
первое вхождение переменной z свободно, а второе – связанное. Переменная x является свободной, а y – связанной. Формальное определение свободных и связанных переменных следующее:
1) все вхождения переменных в атомных формулах свободны;
2) свободные вхождения x в Øq есть в точности свободные вхождения x в q;
3) свободные вхождения x в 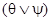 состоят из свободных вхождений x в q и свободных вхождений x в y;
состоят из свободных вхождений x в q и свободных вхождений x в y;
4) если x и y – различные переменные, то свободные вхождения x в формулу
$ y q соответствуют свободным вхождениям x в формулу q;
5) в формуле $ x q нет свободных вхождений переменной x.
Запись: q(x) указывает на то, что формула q содержит свободные вхождения переменной x. Если c – символ константы, то q(с) означает формулу, полученную заменой всех свободных вхождений x в q на с. Например, если q(x) = $y((y = x) & " x (x = y)), то q(c) = $y((y = c) & " x (x = y).
Мы пишем: 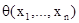 для указания того, что q содержит свободные переменные среди
для указания того, что q содержит свободные переменные среди 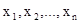 . Применяется запись:
. Применяется запись: 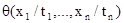 для обозначения формулы, в которой все свободные вхождения каждой из переменных
для обозначения формулы, в которой все свободные вхождения каждой из переменных 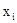 формулы q заменяются на терм
формулы q заменяются на терм 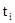 ,
, 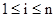 . Таким образом, q(с) является сокращением обозначения q(х/с).
. Таким образом, q(с) является сокращением обозначения q(х/с).
Формула, не содержащая свободных переменных, называется предложением.
Может случиться, что при замене переменной термом нарушается очевидный принцип, согласно которому замена переменной в равных формулах даёт равные формулы. Например, пусть t = f(y), q(z) = $y(y < z). Тогда после замены получаем: 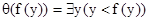 . С другой стороны, q(z) = $x(x < z), и, значит,
. С другой стороны, q(z) = $x(x < z), и, значит, 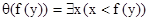 . Получаем не равные формулы. Поэтому перед подстановкой терма
. Получаем не равные формулы. Поэтому перед подстановкой терма 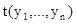 в формулу q(х) связанные переменные, содержащиеся в
в формулу q(х) связанные переменные, содержащиеся в 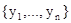 будем переименовывать на символы, не встречающиеся в
будем переименовывать на символы, не встречающиеся в 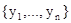 .
.
Другой выход следующий: терм t называется свободным для переменной x в формуле q(х), если никакое свободное вхождение x в q не лежит в области действия кванторов 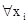 и
и 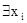 , где
, где 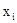 входит в t. В этом случае замена q(х/t) допускается.
входит в t. В этом случае замена q(х/t) допускается.
При подстановках констант противоречия не возникают.
Замечание. Применяемые в анализе и алгебре обозначения: 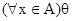 и
и 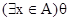 служат сокращениями соответственно формул
служат сокращениями соответственно формул 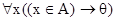 и
и 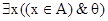 . Например,
. Например, 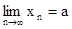 будет определяться формулой:
будет определяться формулой: 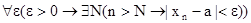 .
.
Дата добавления: 2016-09-20; просмотров: 1609;
