Исчисление предикатов

Для того чтобы определить формальную теорию, связанную с языком первого порядка, введём логические аксиомы и правила вывода языка L. Логические аксиомы подразделяются на 3 группы:

1) Аксиомы предложений: всякая формула q языка L, которая может быт получена из некоторой тавтологии исчисления высказываний K (описанного в разд. 3 с помощью аксиом К1 – К10) в результате подстановки формул языка L на место высказывательных символов, есть логическая аксиома языка L. Всякая такая формула называется тавтологией языка первого порядка L.

2) Аксиомы кванторов

· если q и y – формулы языка L, то имеют место следующие аксиомы:

("x (q ® y)) ® (q ® "x y), если х не входит свободно в q;

("x (q ® y)) ® (($ x q) ® y), если х не входит свободно в y;

· для каждой формулы q(х) и терма t, свободного для x, имеют место кванторные аксиомы:

" х q(х) ® q(t);

q(t) ® $ х q(х).

3) Аксиомы равенства

t = t для любого терма t;

(t = s) & q(t) ® q(s), для любых формул q(х) и термов s, t, для которых х свободна в q, а s и t свободны для х (здесь q(t) означает формулу q(x/t)).

Правила вывода

(MP) Из формул q и q ® y выводится y (Modus Ponens).

(Gen) Из формулы q выводится " x q (правило обобщения).

Таким образом, определена формальная теория, (разд.3.4), в которой есть формулы, аксиомы и правила вывода. Эта теория называется исчислением предикатов L.

Запись: å 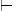q означает, что существует вывод формулы q из логических аксиом и формул из множества å. Если Æ 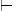q, то q – теорема исчисления предикатов L. Множество å называется противоречивым, если для каждой формулы q языка L существует вывод: å 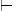q. В противном случае å называется непротиворечивым. Предложение q называется непротиворечивым, если множество {q} непротиворечиво. Множество формул å называется максимально непротиворечивым, если оно не является собственным подмножеством некоторого непротиворечивого множества.

Легко доказать следующие свойства непротиворечивых множеств:

1) Множество å непротиворечиво, если и только если каждое его конечное подмножество непротиворечиво.

2) Пусть q – предложение. Тогда множество å È {q} противоречиво, если и только если å 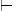Øq.

3) Пусть å – максимально непротиворечивое множество. Тогда для любых предложений q и y имеет место:

(i) å 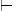q, если и только если q Î å;

(ii) q Ï å, если и только если Øq Î å;

(iii) (q & y) Î å, если и только если q Î å и y Î å;

4) Каждое непротиворечивое множество предложений содержится в некотором максимальном непротиворечивом множестве предложений.

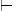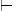Теорема (о непротиворечивости исчисления предикатов). Нет формул q исчисления предикатов L, для которых существуют выводы: q и Øq.

Доказательство. Каждой формуле q поставим в соответствие формулу h(q) исчисления высказываний K, множество символов P которого состоит из предикатов RÎL. Формулу h(q) определим по индукции:

1) 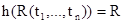для атомных формул;

2) , ,

,

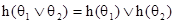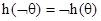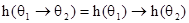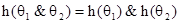, для любых формул ;

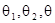3) h("xq) = h(q), h($xq) = h(q).

Для всякой логической аксиомы q формула h(q) будет тавтологией в K. Если бы для некоторой формулы q существовали выводы 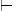q и 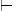Øq, то формулы h(q) и Øh(q) были бы тавтологиями в исчислении высказываний. Поскольку исчисление высказываний непротиворечиво, это невозможно. Стало быть, нет формул q, для которых существуют выводы: 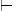q и Øq.