Исчисление высказываний L
Алфавитом называется произвольное множество. Его элементы называются символами. Произвольная конечная последовательность символов называется словом. Слово может быть пустым.
Исчисление высказываний L определяется следующим образом:
Его алфавит состоит из символов 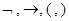 , называемых логическими,и из символов, принадлежащих произвольному множеству Р, называемых нелогическими символами или буквами.
, называемых логическими,и из символов, принадлежащих произвольному множеству Р, называемых нелогическими символами или буквами.
Синтаксис исчисления L определяется с помощью наименьшего подмножества S множества слов, такого, что
1) Р 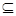 S;
S;
2) Если A 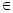 S и B
S и B 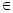 S , то
S , то 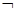 A
A 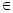 S и (A
S и (A  B)
B) 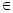 S.
S.
Элементы множества S называются (пропозициональными) формулами. Таким образом, формулами называются слова, определяемые по индукции с помощью правил 1 – 2 из логических и нелогических символов.
Аксиомами исчисления L называются формулы:
(A1) A  (B
(B  A),
A),
(A2) (A  (B
(B  C))
C))  ((A
((A  B)
B)  (A
(A  C)),
C)),
(A3) ( 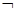 B
B 
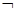 A)
A)  ((
(( 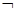 B
B  A)
A)  B).
B).
Здесь A, B, C – произвольные формулы. Поэтому в действительности мы имеем бесконечное множество аксиом, в каждой из групп A1, A2 и A3.
Правилом выводаModus Ponens называется множество троек формул (A,A  B,B), которое позволяет паре формул (A,A
B,B), которое позволяет паре формул (A,A  B) поставить в соответствие формулу B, называющуюся непосредственным следствием этих формул. Правило вывода Modus Ponens обозначается через MP и записывается, как
B) поставить в соответствие формулу B, называющуюся непосредственным следствием этих формул. Правило вывода Modus Ponens обозначается через MP и записывается, как
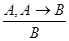 MP
MP
Формула A называется выводимой в исчислении L из формул X1, X2, …, Xk, если существует последовательность формул: A1, A2, A3, …, An, такая, что для каждого 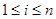 формула Ai является либо аксиомой исчисления L, либо элементом множества {X1, …, Xk} , либо непосредственным следствием формул Ap и Aq, при некоторых
формула Ai является либо аксиомой исчисления L, либо элементом множества {X1, …, Xk} , либо непосредственным следствием формул Ap и Aq, при некоторых
1 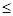 p, q
p, q 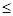 i-1. В этом случае последовательность: A1, A2, A3, …, An называется выводом формулы A. Для обозначения выводимости формулы A в исчислении L из формул X1, …, Xk применяется запись:
i-1. В этом случае последовательность: A1, A2, A3, …, An называется выводом формулы A. Для обозначения выводимости формулы A в исчислении L из формул X1, …, Xk применяется запись:
X1, X2, …, Xk  L A .
L A .
Если для вывода формулы A достаточно аксиом, то А называется теоремой теории L, а выводимость из пустого множества формул записывается, как
 L А .
L А .
Лемма. Имеет место теорема  L А
L А  А.
А.
Доказательство. Построим вывод формулы А  А из аксиом (А1) – (А3) следующим образом:
А из аксиом (А1) – (А3) следующим образом:
А1 будет аксиомой (А2) для формул А, B = (А  А), С = А;
А), С = А;
А2 будет аксиомой (А1) для формул А, В = (А  А);
А);
получим:
А1=(А  ((А
((А  А)
А)  А))
А))  ((А
((А  (А
(А  А))
А))  (А
(А  А)),
А)),
А2=А  ((А
((А  А)
А)  А).
А).
Применяя правило вывода 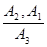 MP , будем иметь непосредственное следствие формул A2 и A1:
MP , будем иметь непосредственное следствие формул A2 и A1:
А3=(А  (А
(А  А))
А))  (А
(А  А).
А).
Следующая формула получается из аксиомы (А1) подстановкой В = А:
А4=А  (А
(А  А).
А).
Применяя правило вывода 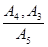 MP, получим:
MP, получим:
А5 = А  А.
А.
Последовательность формул: A1, A2, A3, А4, А5 = (А  А) является искомым выводом формулы А
А) является искомым выводом формулы А  А.
А.
Теорема о дедукции
Пусть Г – множество формул. Запись Г  L А означает, что существует конечная последовательность формул Xi
L А означает, что существует конечная последовательность формул Xi 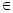 Г,
Г, 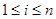 , такая, что X1, X2, …,Xn
, такая, что X1, X2, …,Xn  L A. Вместо Г
L A. Вместо Г 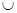 {X}
{X}  L А будем писать Г, X
L А будем писать Г, X  L А. Легко видеть, что из Г
L А. Легко видеть, что из Г  L (А
L (А  В) следует существование вывода Г, А
В) следует существование вывода Г, А  L В. Верно и обратное утверждение:
L В. Верно и обратное утверждение:
Теорема (о дедукции). Пусть Г – множество формул исчисления L; А и В – формулы, и пусть
Г, А  L В.
L В.
Тогда Г  L (А
L (А  В). В частности, при пустом Г, из выводимости А
В). В частности, при пустом Г, из выводимости А  L В вытекает теорема:
L В вытекает теорема:  L А
L А  В.
В.
Доказательство. Пусть В1, В2, …, Вn = В – вывод формулы из формул, принадлежащих множеству Г 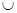 {A}. Докажем с помощью индукции по i, что Г
{A}. Докажем с помощью индукции по i, что Г  L (А
L (А  Вi), а затем применим это к i = n, чтобы получить Г
Вi), а затем применим это к i = n, чтобы получить Г  L (А
L (А  В). При i = 1 имеем В1
В). При i = 1 имеем В1 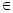 Г, либо В1 = А, либо В1 – аксиома. Если В1
Г, либо В1 = А, либо В1 – аксиома. Если В1 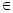 Г, либо В1 – аксиома, тогда получаем с помощью аксиомы (А1) формулу В1
Г, либо В1 – аксиома, тогда получаем с помощью аксиомы (А1) формулу В1  (А
(А  В1). Применение MP к В1 и В1
В1). Применение MP к В1 и В1  (A
(A  В1) дает вывод для А
В1) дает вывод для А  В1 из Г. Если же В1 = А, то имеем:
В1 из Г. Если же В1 = А, то имеем:  L (А
L (А  В1) по доказанной лемме о том, что верна теорема
В1) по доказанной лемме о том, что верна теорема  L А
L А  А.
А.
Докажем теперь: Г  L (А
L (А  Вi) при i > 1, предполагая, что выводимость
Вi) при i > 1, предполагая, что выводимость
Г  L (А
L (А  Вк) уже доказана для всех k < i.
Вк) уже доказана для всех k < i.
Для Вi имеем 4 возможности: Вi 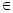 Г; Вi – аксиома; Вi = А; Вi непосредственно следует из Вj и Вm, при некоторых j, m
Г; Вi – аксиома; Вi = А; Вi непосредственно следует из Вj и Вm, при некоторых j, m 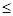 i-1. В первых трёх случаях Г
i-1. В первых трёх случаях Г  L А
L А  Вi доказывается так же, как при i = 1. В четвёртом случае формула Вm равна формуле (Вj
Вi доказывается так же, как при i = 1. В четвёртом случае формула Вm равна формуле (Вj  Вi), и согласно предположению индукции имеем:
Вi), и согласно предположению индукции имеем:
Г  L (А
L (А  Вj) и Г
Вj) и Г  L (А
L (А  (Вj
(Вj  Вi)),
Вi)),
ибо (Вj  Вi)=Вm. По аксиоме (А2) верно
Вi)=Вm. По аксиоме (А2) верно
 L (А
L (А  (Вj
(Вj  Вi))
Вi))  ((А
((А  Вj)
Вj)  (А
(А  Вi)).
Вi)).
Применение
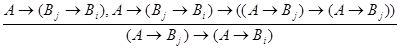 MP
MP
приводит к выводу Г  L (А
L (А  Вj)
Вj)  (А
(А  Вi). Из этого вывода и вывода Г
Вi). Из этого вывода и вывода Г
 L (А
L (А  Вj) с помощью Modus Ponens получаем:
Вj) с помощью Modus Ponens получаем:
Г  L (А
L (А  Вi).
Вi).
Таким образом, Г  L (А
L (А  Вi), для всех i = 1,…,n. В частности, при i = n, получаем:
Вi), для всех i = 1,…,n. В частности, при i = n, получаем:
Г  L (А
L (А  В),
В),
что и требовалось доказать.
Дата добавления: 2016-09-20; просмотров: 1593;
