Реализация функций формулами

Пусть 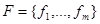– множество булевых функций. Понятие формулы над F определяется индуктивно:

1. Каждая переменная 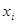и каждая булева функция из F являются формулами над F.

2. Если 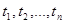– формулы над F, то для каждой функции 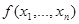из F выражение вида 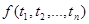являются формулой над F.

Каждой формуле над F соответствует булева функция, которая называется интерпретацией этой формулы. Интерпретацию, как и формулу, можно определить индуктивно:

1. Интерпретация формулы 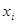сопоставляет элементу 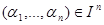элемент .

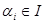2. Интерпретация формулы 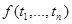принимает значения 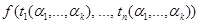, где функции 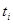дополняются, в случае необходимости, фиктивными переменными.

Пример

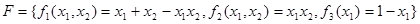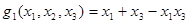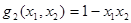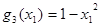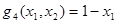Пусть . Тогда , , и – формулы над F, ибо

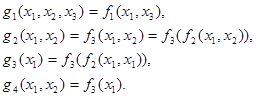
Подставляя 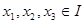в формулы, получим значения интерпретаций этих формул.

Если интерпретацией формулы g является булева функция f, то формула g называется реализацией функции f. Две формулы называются равносильными, если их интерпретации равны.

Например, формулы 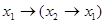и 1, над 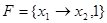, равносильны, ибо функция 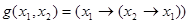принимает значения 1, для всех .

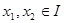Множество классов равносильных формул составляют булеву алгебру относительно операций:

& , Ú , Ø,

которая называется алгеброй Линденбаума – Тарского.

В следующем разделе будет доказано, что все булевы функции реализуемы формулами над 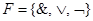, поэтому классы равных булевых функций можно рассматривать как элементы этой булевой алгебры.