Совершенная дизъюнктивная нормальная форма

Теорема. Каждая булева функция 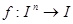реализуема с помощью формулы над .

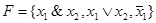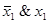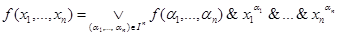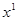Доказательство. Функция 0 реализуема с помощью формулы: . В общем случае имеет место равенство: , где обозначает 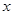, а 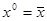. Здесь 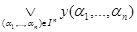обозначает логическую сумму всех значений функции 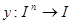. Это приводит к равенству, доказывающему теорему: .

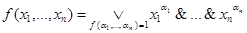Правая часть этого равенства называется совершенной дизъюнктивной нормальной формой (СДНФ).

Пример 1

Найдем СДНФ для функции 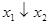. С этой целью составим таблицу истинности:

Поскольку лишь на элементе 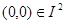значение функции 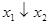равно 1, то .

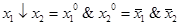Конъюнктивная нормальная форма определяется как конъюнкция формул вида: 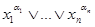. В силу равенств 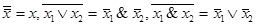получаем соотношение:

.

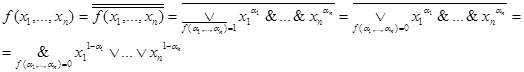Это представление функции f называется ее совершенной конъюнктивной нормальной формой (СКНФ).

Пример 2

Найдем СКНФ функции . Составим таблицу истинности:

Так как 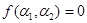лишь в случае 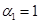и 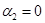, то СКНФ будет равна: 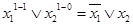. Заметим, что СКНФ формулы 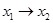будет равна: 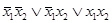. Система булевых функций F называется полной, если каждая булева функция реализуема с помощью формулы над F. Поскольку 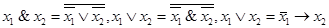, то имеет место следствие.

Следствие. Системы функций 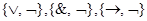являются полными.