Несущественные переменные и равенство функций
Для того чтобы производить операции над функциями, например, из функций 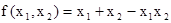 ,
, 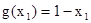 , получить функцию
, получить функцию 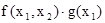 , удобно предполагать, что области определения функций
, удобно предполагать, что области определения функций 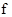 и
и 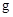 совпадают. С этой целью вводиться понятие несущественной переменной. В данном примере функция
совпадают. С этой целью вводиться понятие несущественной переменной. В данном примере функция 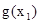 рассматривается как функция от
рассматривается как функция от 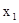 и
и 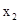 , для которой переменная
, для которой переменная 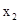 – несущественная.
– несущественная.
Определение. Функция 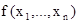 зависит существенным образом от аргумента
зависит существенным образом от аргумента 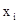 , если существуют такие значения аргументов
, если существуют такие значения аргументов 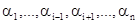 , что
, что 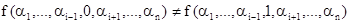 . В противном случае переменная
. В противном случае переменная 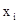 называется несущественной или фиктивной. Две булевы функции называются равными, если одна из другой получается введением или удалением несущественных переменных.
называется несущественной или фиктивной. Две булевы функции называются равными, если одна из другой получается введением или удалением несущественных переменных.
Несущественные переменные удаляются следующим образом:
Сначала строится таблица значений функции 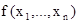 . Затем перебираются пары строк аргументов, на которых значения функции
. Затем перебираются пары строк аргументов, на которых значения функции 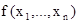 совпадают, и отмечается
совпадают, и отмечается 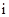 -й элемент строк вида
-й элемент строк вида
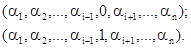
Если, в результате, все элементы некоторого столбца 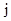 окажутся отмеченными, то
окажутся отмеченными, то 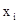 будет несущественной переменной.
будет несущественной переменной.
Пример
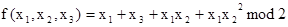 . Здесь
. Здесь 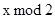 обозначает остаток от деления
обозначает остаток от деления 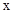 на 2. Составим таблицу значений:
на 2. Составим таблицу значений:
| x1 | x2 | x3 | f | |
| 0 | ||||
| 0 | ||||
| 1 | ||||
| 1 | ||||
| 0 | ||||
| 0 | ||||
| 1 | ||||
| 1 |
Строку 1 сравниваем со строками, в которых 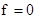 . Отмечаем элементы 2-го столбца строк 1 и 3. То же самое проделываем с остальными строками. Отмечаем элементы 2-го столбца строк 2 и 4, 5 и 7, 6 и 8. Поскольку все элементы столбца 2 отмечены, то
. Отмечаем элементы 2-го столбца строк 1 и 3. То же самое проделываем с остальными строками. Отмечаем элементы 2-го столбца строк 2 и 4, 5 и 7, 6 и 8. Поскольку все элементы столбца 2 отмечены, то 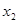 – несущественная переменная. Вычеркивая второй столбец, получаем таблицу значений некоторой функции
– несущественная переменная. Вычеркивая второй столбец, получаем таблицу значений некоторой функции 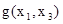 , равной
, равной 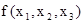 :
:
| x1 | x2 | g |
Функция 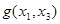 фиктивных переменных не имеет. В общем случае некоторые строки таблицы значений могут отличаться лишь одним элементом, а функция может не иметь фиктивных переменных. Например, функция
фиктивных переменных не имеет. В общем случае некоторые строки таблицы значений могут отличаться лишь одним элементом, а функция может не иметь фиктивных переменных. Например, функция 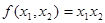 имеет таблицу:
имеет таблицу:
| x1 | x2 | f |
| 0 | 0 | |
| 1 | ||
| 1 | ||
и не имеет фиктивных элементов.
Дата добавления: 2016-09-20; просмотров: 1236;
