Аксиома выбора и сравнения мощностей
Следующее утверждение справедливо в предположении аксиомы выбора и вместе с теоремой Кантора-Шредера-Бернштейна (разд. 1.7) позволяет установить, что для любых множеств X и Y имеет место одно из соотношений:
|X| < |Y|, |X| = |Y|, |X| > |Y|.
Теорема. Пусть X и Y – множества. Тогда |X| £ |Y| или |Y| £ |X|.
Доказательство. Пусть T – множество пар (A. f), состоящее из подмножеств
A Í X и инъекций f : A à Y. Определим на T отношение порядка, полагая для
(A1, f1) и (A2. f2) из T выполненным отношение (A1, f1) £ (A2. f2), если A1 < A2 и 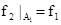 . Для произвольной цепи C Í T существует пара (B, g), состоящая из
. Для произвольной цепи C Í T существует пара (B, g), состоящая из 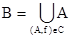 и отображения g : B à Y, заданного как g(x) = f(x), если (A, f) – такая пара из T, что x Î A. Эта пара (B, g) будет ограничивать сверху цепь С. Значит, любая цепь С ограничена сверху в Т, и в Т существует, по крайней мере, один элемент, который мы обозначим через (A, f). Если A ¹ X и Imf ¹ Y, то инъекцию f можно доопределить на некотором x Î X \ A и получить таким образом элемент из T, больший чем
и отображения g : B à Y, заданного как g(x) = f(x), если (A, f) – такая пара из T, что x Î A. Эта пара (B, g) будет ограничивать сверху цепь С. Значит, любая цепь С ограничена сверху в Т, и в Т существует, по крайней мере, один элемент, который мы обозначим через (A, f). Если A ¹ X и Imf ¹ Y, то инъекцию f можно доопределить на некотором x Î X \ A и получить таким образом элемент из T, больший чем
(A, f). Это противоречие показывает, что либо A ¹ X и Imf = Y, либо A = X. В первом случае f осуществляет биекцию некоторого подмножества из X с множеством Y, и, значит, имеет место |Y| £ |X|. Во втором случае |X| £ |Y|. Теорема доказана.
Замечание. В действительности эта теорема равносильна аксиоме выбора и, стало быть, может быть принята в качестве аксиомы.
Счетные множества
Мощностью множества X будем называть совокупность всех множеств Y таких, что |X| = |Y|. Обозначим мощность тем же символом |X|. Эта совокупность не является множеством, тем не менее, можно доказать, что из неё можно выбрать канонический представитель и взять его за определение мощности.
Множество X называется конечным, если существует n Î w такое, что |X| = |n|. Множество X называется счетным, если |X| = |w|. Например, множество {0, 3, 5} конечно, а множество всех четных натуральных чисел {0, 2, 4, …} счётно.
Упражнение 1
Доказать, что множество положительных рациональных чисел Q+ – счётно.
Указание. Каждое положительное рациональное число можно представить как несократимую дробь m/n. Отсюда существует инъекция Q+ à w ´ w, сопоставляющая дроби m/n пару (m, n), и, значит, |Q+| £ |w ´ w|. Счётность множества w ´ w доказывается стандартным способом:
Пары (m, n) располагаем в таблицу:
(0, 0) (1, 0) (2, 0) (3, 0) …
(0, 1) (1, 1) (2, 1) (3, 1) …
(0, 2) (1, 2) (2, 2) (3, 2) …
… … … …
Затем их выстраиваем в последовательность: (0, 0), (1, 0), (0, 1), (0, 2), (1, 1), (2, 0), (3, 0), (2,1), (1,2), … Сопоставляя каждому n Îw n-й член этой последовательности, получаем биекцию между w и w ´ w. Поскольку каждое бесконечное подмножество из w счётно, отсюда получаем счётность Q+.
Упражнение 2
Доказать, что объединение двух счётных множеств счётно.
Упражнение 3
Пользуясь решениями предыдущих упражнений 2 и 1, доказать счётность всех рациональных чисел.
По теореме Кантора, |w| < |P(w)|, поэтому P(w) – несчётно.
Упражнение 4
Доказать, что множество действительных чисел 0 < x < 1 несчётно.
Доказательство провести методом диагонализации. Каждое число представляем в виде бесконечной десятичной дроби: 0.a1a2a3,… состоящей из цифр и не имеющей в периоде 9. Предположим, что множество таких дробей счётно. Тогда их можно расположить в виде списка строк:
0 . a11 a12 a13 a14…
0 . a21 a22 a23 a24…
0 . a31 a32 a33 a34…
…
Рассмотрим последовательность цифр: b1 ¹ a11, b2 ¹ a22, b3 ¹ a33, …, не равных 9. Тогда число 0.b1b2b3 … не содержится в списке, хотя находится в интервале (0, 1). Значит, все действительные числа из этого интервала невозможно занумеровать с помощью натуральных чисел.
Булевы алгебры
Бинарной операцией на множестве A называется произвольное отображение 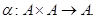 Значения a(a, b) на (a,b) Î A ´ A обычно записываются в инфиксной форме: a a b.
Значения a(a, b) на (a,b) Î A ´ A обычно записываются в инфиксной форме: a a b.
Пример 1
Операция сложения +: w ´ w ® w является бинарной операцией на множестве натуральных чисел.
Унарной операцией на множестве A называется произвольное отображение A ® A.
Булевой алгеброй называется непустое множество A, на котором определены две бинарные операции È, Ç и одна унарная операция Ø , удовлетворяющие для всех a, b, c Î A следующим аксиомам:
1) a È b = b È a, a Ç b = b Ç a;
2) a È (b È c) = (a È b) È c, a Ç (b Ç c) = (a Ç b) Ç c;
3) (a Ç b) È b = b, (a È b) Ç b = b;
4) a Ç (b È c) = (a Ç b) È (a Ç c), a È (b Ç c) = (a È b) Ç (a È c);
5) (a Ç Ø a) È b=b, (a È Ø a) Ç b = b.
Таким образом, булева алгебра – это непустое множество и операции, обладающие теми же свойствами, что и операции пересечения, объединения и дополнения подмножеств фиксированного множества.
Пример 2
Под полем множеств понимается непустое множество U подмножеств фиксированного множества X, содержащее вместе с любыми A, B Î U их объединение A È B и пересечение A Ç B, и вместе с любым A Î U – его дополнение X\A. Легко видеть, что U будет булевой алгеброй относительно операций: A È B, A Ç B и ØA = X\A.
Пусть (A, È, Ç, Ø) – булева алгебра. Можно доказать, что для любых a, b Î A верно a È Øa = b È Øb и a Ç Øa = b Ç Øb, и, значит, элементы x È Øx, x Ç Øx не зависят от x. Обозначим x È Øx через 1, а x Ç Øx через 0. Имеют место тождества:
6) a È a = a, a Ç a = a;
7) a È 1 = 1, a Ç 0 = 0;
8) a È 0 = a, a Ç 1 = a;
9) Ø (Ø a) = a;
10) Ø (a Ç b) = (Ø a) È (Ø b), Ø (a È b) = (Ø a) Ç (Ø b).
Докажем, например, свойство 6.
В силу симметричности определения булевой алгебры относительно операций È и Ç, достаточно доказать: a È a = a. Применим аксиомы булевой алгебры:
a = (b Ç a) È a (по аксиоме 3)
= a È (b Ç a) (по аксиоме 1)
= a È (a Ç b) (по аксиоме 1)
= (a È a) Ç (a È a) (по аксиоме 4)
= (a Ç (a È b)) È (a Ç (a È b)) (по аксиоме 4)
= ((b È a) Ç a) È ((b È a) Ç a) (по аксиоме 1)
= a È a, что и требовалось доказать.
Для каждой булевой алгебры существует поле подмножеств некоторого множества и сохраняющая операции объединения, пересечения и дополнения биекция между элементами булевой алгебры и элементами поля подмножеств. Поэтому операции булевой алгебры обладают свойствами, аналогичными свойствам теоретико-множественных операций.
БУЛЕВЫ ФУНКЦИИ
Дата добавления: 2016-09-20; просмотров: 1635;
