Операции над отношениями

Напомним, что отношением между множествами A и B называется произвольное подмножество R Í A ´ B. Поскольку отношения являются подмножествами множества A ´ B, то для них определены операции объединения, пересечения и дополнения 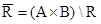. Вместо (x, y) Î R обычно пишут x R y и говорят, что x находится в отношении R с y. Бинарным отношением на A называется подмножество R Í A ´ A.

Например, отношение равенства =, на множестве w натуральных чисел можно понимать как множество пар {(0, 0), (1, 1), (2, 2), …}.

Дополнением этого отношения будет отношение ¹. Отношение < будет множеством пар (x, y), для которых x < y. Объединением отношений < и = будет равно отношению £, а пересечение будет пустым отношением.

Большое значение имеют также операции обращения и композиции отношений.

Для произвольного отношения R Í A ´ B обратным называется отношение 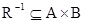, состоящее из пар (b, a), для которых (a, b) Î R. Например, для отношения < на w, обратное отношение <^-1 состоит из пар (y, x) таких, что x < y. Следовательно, .

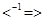Пусть заданы отношения R Í A ´ B и S Í B ´ C. Композицией называется отношение:

S ° R = {(a, c) Î A ´ C: существует b Î B такой, что (a, b) Î R и (b, c) Î S}

Имеют место соотношения:

(T ° S) ° R = T ° (S ° R),

R ° Id_A = Id_B ° R = R,

для любых отношений R Í A ´ B, S Í B ´ C, T Í C ´ D, и отношений равенств
Id_A = {(a, a): a Î A} на A, Id_B = {(b, b): b Î B} на B.