Компактность и полнота языка первого порядка
Теорема компактности для счётных языков была доказана Куртом Гёделем в 1930 году. Анатолий Иванович Мальцев доказал её для произвольных языков первого порядка в 1936 году. Мы будем следовать доказательству Генкина (1949 г.).
Напомним, что теории – это множества предложений. Множество предложений å языка L называется конечно выполнимым, если каждое конечное подмножество из å имеет модель. Множество å – полное, если для каждого предложения q либо q Î å, либо Øq Î å.
Лемма 1.Для каждого конечно выполнимого множества å предложений языка первого порядка существует полное конечно выполнимое множество предложений 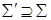 .
.
Доказательство. Пусть B = {Q : Q Ê å и Q – конечно выполнимо}. Легко видеть, что (B, Í) удовлетворяет лемме Куратовского-Цорна. Значит, существует максимальное конечно выполнимое 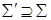 . Для каждого предложения q либо
. Для каждого предложения q либо 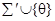 , либо
, либо 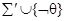 конечно выполнимо. В противном случае существуют конечные
конечно выполнимо. В противном случае существуют конечные 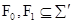 такие, что
такие, что 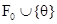 и
и 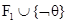 не имеют моделей, хотя
не имеют моделей, хотя 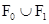 будет иметь некоторую модель А в силу конечной выполнимости å. Для этой модели либо A |= q, либо A |= Øq. Противоречие показывает, что либо
будет иметь некоторую модель А в силу конечной выполнимости å. Для этой модели либо A |= q, либо A |= Øq. Противоречие показывает, что либо 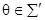 , либо
, либо 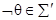 . Следовательно,
. Следовательно, 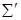 – полное.
– полное.
Лемма 2. Если å – конечно выполнимое множество предложений языка L с одной свободной переменной x, а с – новый символ константы (не принадлежащий L), то å È {($xq(x)) ® q(c)} – конечно выполнимо в языке L È {с}.
Доказательство. Новое предложение ($xq(x)) ® q(c) называется предложением Генкина, а константа с – константой Генкина. Предположим, что å È {($xq(x)) ® q(c)} не является конечно выполнимым. Тогда существует конечное 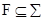 , такое, что
, такое, что
F È {($xq(x)) ® q(c)} не имеет модели. Пусть А – модель языка L, удовлетворяющая F. Так как константа с не принадлежит L, то мы можем интерпретировать её произвольным образом. Если A |= $xq(x), то существует b Î А, для которого A |= 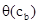 . В этом случае, сопоставляя символу с элемент b, мы расширим модель на L È {c}. Получим A |= q(c), а вместе с тем A |= $xq(x) ® q(c). Если же $xq(x) ложно в модели А, то символу c можно сопоставить любой элемент из А. Во всех случаях модель А будет удовлетворять F È {($xq(x)) ® q(c)}.
. В этом случае, сопоставляя символу с элемент b, мы расширим модель на L È {c}. Получим A |= q(c), а вместе с тем A |= $xq(x) ® q(c). Если же $xq(x) ложно в модели А, то символу c можно сопоставить любой элемент из А. Во всех случаях модель А будет удовлетворять F È {($xq(x)) ® q(c)}.
Определение. Множество å предложений языка L называется множеством Генкина, если для каждой формулы q(x) с единственной свободной переменной х существует такой символ константы с Î L, что
(($xq(x)) ® q(c)) Î å .
Лемма 3. Если å – конечно выполнимое множество предложений языка L, то существуют такие 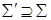 и
и 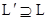 , что å¢ является конечно выполнимым множеством Генкина предложений языка L¢.
, что å¢ является конечно выполнимым множеством Генкина предложений языка L¢.
Доказательство. Для любого множества å предложений языка L положим:
å* = å È {$xq(x) ® q(cq) : q(x) – формула языка L с одной свободной переменной}. Язык теории å* содержит новый символ константы cq для каждой формулы q(x). Применяя к конечным подмножествам теории å* лемму 2, получим конечную выполнимость множества å*. Далее положим: å0 = å и 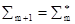 для всех m Î w. Тогда множество
для всех m Î w. Тогда множество 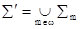 будет множеством Генкина. Оно конечно выполнимо как объединение цепи конечно выполнимых множеств.
будет множеством Генкина. Оно конечно выполнимо как объединение цепи конечно выполнимых множеств.
Дата добавления: 2016-09-20; просмотров: 776;
