Полнота теории первого порядка

Кроме исчисления предикатов существуют другие формальные теории, связанные с языком первого порядка. Мы рассмотрим исчисление предикатов. Наиболее простая из них – исчисление ММ. Логические аксиомы в этой системе – предложения q, истинные в любой модели языка первого порядка L. Правило вывода одно – Modus Ponens. Мы будем опираться далее на равносильность этой формальной теории исчислению предикатов, которая в действительности вытекает из теоремы Гёделя о полноте исчисления предикатов.

Теорема о полноте теории первого порядка. Пусть заданы произвольные множества предложений å и предложение q языка L. Вывод å 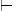q существует тогда и только тогда, когда каждая модель теории å удовлетворяет предложению q .

Доказательство. В случае å 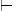q и A |= å утверждение A |= q доказывается очевидным образом с помощью индукции по длине вывода å 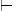q (теорема о корректности). Пусть, наоборот, каждая модель A |= å удовлетворяет q. Так как всякая модель å является моделью для q, то множество предложений å È {Øq} не имеет моделей. По теореме компактности существует такое конечное подмножество {q₁, …, q_n} Í å, что {q₁, …, q_n, Øq} не имеет моделей. Отсюда Ø (q₁ & … & q_n & Øq) – тавтология исчисления ММ. Значит, имеет место логическая аксиома: q₁ ® (q₂ ® (… ® (q_n ® q) …))), из которой будет вытекать вывод: å 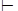q.

Упрощение формул

Наша задача: привести произвольную формулу к бескванторной форме. Это можно решить приведением к пренексной нормальной форме с последующей элиминацией кванторов и расширением исходного языка.