Алгоритм унификации термов с использованием стека
Вход: термы s, t.
Выход: подстановка h, записанная как список пар 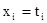 , если t и s обладают наибольшим общим унификатором. Процедура возвращает отказ, если унификаторов нет.
, если t и s обладают наибольшим общим унификатором. Процедура возвращает отказ, если унификаторов нет.
Действия: h = Æ; запомнить пару (s = t) в стек;
Пока стек не пуст, выполнять цикл:
Тело цикла: Извлечь из стека пару термов (s = t) и произвести одно из следующих действий, в зависимости от выполнения одного из условий
I если s – переменная, t – терм, не содержащий вхождений s, то все вхождения переменной s в стеке заменяются на t и все вхождения s в h заменяются на t, затем подстановка s = t добавляется к списку подстановок в h;
II если t – переменная, а s – терм, то произвести действия, как в I, поменяв ролями s и t (к h добавляется пара t = s);
III если s и t – составные термы, 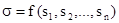 и
и 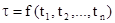 , то все пары
, то все пары 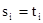 , 1 £ i £ n, запоминаются в стек;
, 1 £ i £ n, запоминаются в стек;
IV если s и t – одинаковые символы констант или переменных, то ничего не делать;
V во всех остальных случаях производится выход из цикла и возвращается отказ.
Конец тела цикла.
Если выход из цикла произошёл не после выполнения условия V, то h содержит элементы 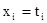 искомой подстановки.
искомой подстановки.
Пример
s = (a Ç b) È ((a Ç b) Ç d), t = (a Ç b) È (c Ç (a Ç b)).
1) Устанавливаем h = Æ; запоминаем в стек пару (s = t);
2) извлекаем (s = t) из стека, имеет место случай III, запоминаем в стек пары 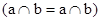 и ((a Ç b) Ç d = c Ç (a Ç b));
и ((a Ç b) Ç d = c Ç (a Ç b));
3) извлекаем из стека ((a Ç b) Ç d = c Ç (a Ç b)), имеет место случай III, запоминаем в стек (a Ç b = c) и (d = a Ç b);
4) извлекаем из стека (d = a Ç b), имеет место случай I, h = {(d = a Ç b)};
5) извлекаем из стека (a Ç b = c), имеет место случай II, 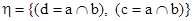 ;
;
6) извлекаем из стека 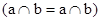 , изменений в h нет;
, изменений в h нет;
7) стек пуст, возвращаем 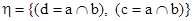 .
.
Система уравнений
Пусть задано несколько пар термов 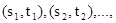
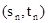 и необходимо найти подстановку w, которая превращает все пары термов
и необходимо найти подстановку w, которая превращает все пары термов 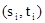 в равные
в равные 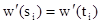 . Эта задача называется системой уравнений:
. Эта задача называется системой уравнений: 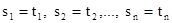 .
.
Унификатором системы уравнений называется подстановка v, которая является унификатором пар 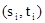 для всех 1 £ i £ n. Система уравнений
для всех 1 £ i £ n. Система уравнений 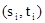 , 1 £ i £ n, называется находящейся в разрешённой форме, если каждое из этих уравнений имеет вид:
, 1 £ i £ n, называется находящейся в разрешённой форме, если каждое из этих уравнений имеет вид: 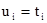 для некоторого элемента
для некоторого элемента 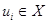 , причём переменная
, причём переменная 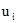 не входит в терм
не входит в терм 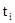 ни при каком i. Такая система имеет унификатором подстановку:
ни при каком i. Такая система имеет унификатором подстановку: 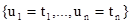 , которая будет наиболее общим унификатором этой системы. Редукцией термов называется замена уравнения
, которая будет наиболее общим унификатором этой системы. Редукцией термов называется замена уравнения 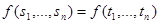 системой уравнений:
системой уравнений: 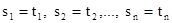 .
.
Дата добавления: 2016-09-20; просмотров: 1801;
