Устойчивость. Устойчивостью на курсе называется способность суд­на сохранять направление прямолинейного движения. Различают два вида устойчивости: собственную и эксплуатационную. 3 страница

Для наглядной оценки адекватности рассматриваемой математи­ческой модели ниже использованы результаты натурных испытаний торможения теплохода «Большевик М. Томас» водоизмещением 22 850 т.

На рис. 3.3 показано пассивное торможение судна ПХПм—Стоп, а на рис. 3.4 — торможение с реверсированием двигателя СХП—ПХЗ. Экспериментальные измерения пути и скорости показаны на обоих

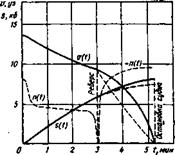Рис. 3.4. Графики торможения теплохо­да «Большевик М. Томас» с реверсиро­ванием двигателя

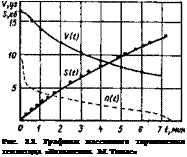рисунках черными точками, а графики s(t) и V(t), рассчитанные по формулам — сплошными линиями. Момент реверсирования (см. рис. 3.4) указан вертикальной штриховой линией. На обоих рисунках при­ведены также графики частоты вращения винта, построенные по ре­зультатам экспериментальных измерений.

На участке активного торможения от момента реверсирования до остановки судна (см рис. 3.4) для сравнения показаны штриховыми линиями также графики пути и скорости, построенные по формулам

(3.25) и (3.26).

Помимо описанных, существует еще ряд моделей, из которых можно отметить линейную математическую модель, в которой теку­щее значение силы сопротивления воды принято пропорциональным скорости судна в первой степени, т. е. R=KV (К — коэффициент со­противления при линейной зависимости, кг/с), а сила упора — посто­янной (Р,.= Р=const).

Имеющиеся результаты натурных экспериментов в виде элемен­тов пассивного и активного торможения по каждому испытанному судну позволяют получить статистические данные точности расчетных значений путей пассивного и активного торможения для каждой ма­тематической модели.

Как известно, в общем случае торможения полный тормозной путь содержит участки пассивного и активного торможения (второй и тре­тий периоды). Точность полного тормозного пути в соответствии с теорией ошибок можно оценивать по формуле

(3.39)

где Мот -относительное среднее квадратическое отклонение (СКО) полного тор­мозного пути, %;

_отн — относительные СКО соответственно пассивного и активного тормозных путей, %;

s^N

— отношение пассивного участка к полному тормозному пути;

m

“Тг —отношение активного участка к полному тормозному пути\

Путь первого периода s¹ (прохождение команды) из-за его мало­сти на оценку точности практически не влияет.

Отношение i—. зависит от типа двигателя и его реверсивного

устройства, а также от начальной скорости судна. В реальных усло­виях это отношение находится в большинстве случаев в пределах 0,15-7-0,75. Для данных значений в табл. 3.1 приведены результаты оценки точности рассмотренных математических моделей для пассив­ных, активных и полных тормозных путей, выполненные на базе на­турных испытаний торможения с полного и полного маневренного хода на 16 различных судах с проведением надежных траекторных изме­рений.

Напомним, что при оценке точности расчетные тормозные пути определялись с использованием значений коэффициента сопротивления и силы упора винта, найденных из условия равенства между расчет­ным к экспериментальным временем торможения. Поэтому приведен­ные в табл. 3.1 оценки характеризуют потенциальную точность, с ко­торой каждая модель способна описывать процесс торможения судна при условии использования оптимальных значений коэффициента со­противления и силы упора винта.

Любая из рассмотренных математических моделей может быть использована для расчета ИТХ, если известны значения коэффициен­та сопротивления и силы упора винта для каждого конкретного судна при заданных условиях торможения. Эти необходимые значения могут быть найдены какими-то расчетными или экспериментально-расчетны­ми способами. Поскольку получаемые таким путем значения коэффи­циента сопротивления и силы упора винта будут содержать неизбеж­ные погрешности, т. е. не будут оптимальными, то ИТХ, полученные с их использованием, будут характеризоваться (статистически) боль­шими погрешностями, чем те, которые указаны в табл. 3.1.

Контрольные вопросы. 1. Каковы особенности реверсирования главного двигате­ля на теплоходах с гребным винтом фиксированного шага? 2. Из каких периодов в общем случае состоит процесс торможения судна? 3. Чем отличаются друг от друга основные математические модели торможения судна? 4. Как изменяется полезная си­ла упора винта в процессе активного торможения? 5. Как влияет загрузка судна на время и путь его торможения? в. Чем объясняется зависимость максимальной силы упора винта при активном торможении от осадки судна?

Глава 4.УПРАВЛЕНИЕ СУДНОМ В УСЛОВИЯХ ВЕТРА

4.1. Силы и моменты, связанные с воздействием ветра

Сила ветра оценивается в баллах двенадцатибалльной шкалы, при­веденной в МТ-75.

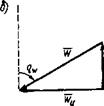
Скорость ветра в судовых условиях измеряется над верхним мос­тиком с помощью анемометра. При этом измеряется так называемая кажущаяся скорость ветра UP, вектор которой представляет собой разность двух векторов — вектора истинного ветра ТГ_И и вектора ско­рости судна Р, т. е.

W = Wh-V. (4.1)

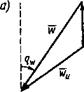
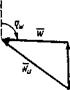
Вектор кажущегося ветра, помимо скорости, характеризуется кур­совым углом qw, т. е. углом между носовой частью ДП и кажущимся направлением ветра. За направление ветра принимается то, откуда ду­ет ветер (ветер дует «в компас»).

Курсовые углы ветра измеряются от 0 до 180° вправо и влево от ДП (курсовые углы правого или левого борта).

Геометрический смысл формулы (4.1) характеризуется векторным треугольником, показанным на рис. 4.1 (а, б, в). Из рисунка видно, что под влиянием движения судна вперед со скоростью V курсовой угол кажущегося ветра будет всегда меньше, чем истинного.

Аэродинамическая сила и ее момент. Равнодействующая сила давления ветра на надводную часть — аэродинамическая сила А не совпадает в общем случае с направлением кажущегося ветра, а откло­няется в сторону траверзного направления (см. п. 1.1).

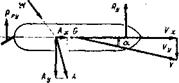
Надводная часть судна находится в потоке воздуха под углом ата­ки, равным курсовому углу кажущегося ветра. При этом на надводной части создается аэродинамическая сила А, имеющая, как показано на рис. 4.2, продольную А_х и поперечную А_у составляющие.

Продольная составляющая А_х влияет на скорость судна, а попе­речная А_у вызывает боковое перемещение судна.

Поперечную аэродинамическую силу (Н) можно рассчитать по формуле

(4.2)

где Со* — безразмерный коэффициент поперечной аэродинамической силы, зависящий от формы надводной части судна и курсового угла кажущегося ветра;

Q_y— боковая площадь парусности (площадь проекции надводной части на ДП), м²;

р_а —■ массовая плотность воздуха (р_в» 1,226 кг/м).

Безразмерный аэродинамический коэффициент С_ау по данным натурных и модельных исследований для разных судов находится обычно в пределах от 0,8 sin q_w до 1,3 sin q_w.

Точка приложения аэродинами­ческой силы в соответствии со свой­ствами крыла смещается от ЦП на­встречу потоку воздуха (см. рис. 4.2), т. е. при носовых курсовых углах вет­ра в сторону носа, а при кормовых курсовых углах — в корму. Величина смещения зависит от курсового угла кажущегося ветра: чем острее угол атаки между ДП и направлением ветра, тем дальше от ЦП сме­щается точка приложения аэродинамической силы. Максимальное сме­щение точки приложения аэродинамической силы (при курсовых углах, близких к 0 и 180°) составляет в среднем приблизительно четверть длины судна, т. е. 0,25L, а при курсовых углах кажущегося ветра, рав­ных 90°, точка приложения аэродинамической силы совпадает с ЦП.

Таким образом, в общем случае на корпус судна действует не только поперечная аэродинамическая сила, вызывающая дрейф судна, но и момент этой силы, стремящийся развернуть судно вокруг верти­кальной оси, проходящей через ЦТ.

Плечо поперечной аэродинамической силы 1_Л относительно ЦТ можно определить по приближенной формуле:

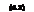7 -о I^е, I ^{<ци 4w}

/_д-0,25+ _L ^

где 7а—- относительное плечо аэродинамической силы, выраженное в долях длины кор-

.к. (‘л- -£);

L—длина судна между перпендикулярами, м;

/цп— отстояние ЦП от Цт, м.

В формуле (4.3) величина /_цп принимается положительной, если ЦП смещен в нос от ЦТ, и отрицательной при его смещении в корму. Знак величины /л укажет соответственно направление смещения точ­ки приложения аэродинамической силы от ЦТ.

Положение ЦП по длине судна /_цп зависит от размеров и распо­ложения надстроек и других надводных частей, а также от диффе­рента судна и его осадки. Площадь парусности и положение ЦП по длине судна можно рассчитать по чертежу бокового вида судна с уче­том масштаба. При этом следует иметь в виду, что положение ЦП значительно изменяется с изменением дифферента судна.

При определении отстояния ЦП от ЦТ для (4.3) необходимо учи­тывать положение ЦТ по длине, которое только при .посадке судна на «ровный киль» приблизительно совпадает с мидель-шпангоутом. Если ЦТ смещен в сторону одной из оконечностей судна, то благодаря диф­ференту ЦП смещается в противоположную сторону, что приводит к существенному изменению /_ц„ и, следовательно, /д.

Аэродинамический момент Мл=Л_у1_л стремится развернуть суд­но относительно вертикальной оси в направлении уваливания навет­ренной оконечности судна.

Гидродинамическая сила и ее момент. Поперечная аэродинамиче­ская сила А_у создает боковое перемещение судна — дрейф со скоро-

стыо V_y, в результате чего корпус судна движется с углом дрейфа а.

В этих условиях корпус судна испытывает сопротивление со стороны воды в виде гидродинамической силы /?, имеющей поперечную состав­ляющую Ry.

Подводная часть судна характеризуется площадью проекции по­груженной части на ДГ1. Эту площадь S_y для приближенных оценок можно принимать равной произведению длины судна между перпен­дикулярами на среднюю осадку.

При движении судна лагом, когда о=90°, точка приложения силы реакции воды (гидродинамической силы Л) носит название цент­ра бокового сопротивления (ЦБС).

Приближенно можно считать, что ЦБС совпадает с центром пло­щади проекции погруженной части судна на ДП, а по длине судна практически совпадает с ЦТ.

При посадке судна на ровный киль ЦБС, как и ЦТ, примерно сов­падает с мидель-шпангоутом, а при наличии дифферента отстояние ЦБС от мидель-шпангоута можно приближенно рассчитать по фор­муле

7- _о,5,

^цвс 3 (1 —d„/d„)

где /ц_БС — расстояние ЦБС от мидель-шпангоута, выраженное в долях длины судна L; ё_ы —- осадка носа, м; dm -- осадка нормы, м.

Знак «—» у 7цбс укажет, что ЦБС смещено в корму от ми- дель-шпангоута, а знак «+» — в нос.

Если угол дрейфа не равен 90°, то точка приложения гидродина­мической силы смещается по ДП в направлении движения, т. е. на­встречу набегающему потоку воды. Если угол дрейфа меньше 90°, то точка приложения смещается от ЦБС в сторону носа, а при угле дрей­фа более 90° — в сторону кормы, т. е. смещение точки приложения гидродинамической силы имеет ту же закономерность, что и для аэро­динамической. Однако величина смещения точки приложения гидро­динамической силы примерно в 2 раза больше, чем аэродинамической при одинаковых углах атаки (а=?»), что объясняется более совер­шенными обводами подводной части и, следовательно, более выражен­ным проявлением свойств крыла.

Плечо поперечной гидродинамической силы относительно ЦТ можно приближенно рассчитывать по формуле

где 1н — относительное плечо поперечной гидродинамической силы, выраженное в до­лях длины корпуса -^rj;

/цвс — отстояние ЦБС от ЦТ, м.

В соответствии с формулой (4.4) точка приложения гидродина­мической силы имеет максимальное смещение при углах дрейфа, близ­ких к 0 и 180°, когда это смещение достигает ±0,51, т. е. точка при­ложения приближается к носовому или кормовому перпендикуляру.

Угол дрейфа, близкий к 180®, судно может иметь при движении назад.

Рис. 4.3. Силы, действующие на суд­но при движении с углом дрейфа

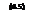Поперечная составляющая гидродинамической силы R_y создает гидродинамический момент M_R относительно вертикальной оси, про­ходящей через ЦТ судна,

M_R =/?* i_R,

Поперечная гидродинамическая сила R_y в Н рассчитывается по формуле*

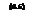Ry-CyZ-SyV*.

где р — массовая плотность забортной воды, кг/м³;

S- — площадь проекции подводной части судна на ДП, м²;

V —* скорость судна относительно воды, м/с;

C_v — безразмерный коэффициент поперечной гидродинамической силы, значение ко-

торого можно выразить приближенной зависимостью 0,23sinct-f l,09sin²cc

(4.7)

(2,16—7d/L)*

где 6 — коэффициент общей полноты; d/L — отношение средней осадки судна к его длине.

Очевидно, что формулы (4.3) и (4.4) структурно подобны. Сле­дует лишь еще раз отметить, что ЦБС располагается по длине судна всегда сравнительно близко от ЦТ, поэтому в практических расчетах допустимо /_ЦБС принимать равным нулю, в то время как /_11П мо­жет иметь значительную величину.

4.2. Ветровой дрейф

Условия движения судна постоянным курсом с углом ветрового дрейфа выражаются вторым и третьим уравнениями системы (1.1), которые для случая установившегося движения, когда инерционные силы и момент равны нулю, можно записать в следующем виде:

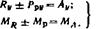
(4.8)

Ветер, дующий со скоростью W под произвольным курсовым уг­лом, воздействует на надводную часть судна силой А, которую в об­щем случае можно разложить (рис. 4.3) на две составляющие: про­дольную А_х и поперечную А_у.

Продольная составляющая А_х, складываясь алгебраически с си­лой сопротивления Я*, увеличивает или уменьшает скорость движе­ния судна V_x. Эта скорость учитывается лагом, поэтому силу А_х мож­но не рассматривать.

Сила А_у, действующая перпендикулярно ДП, заставляет судно смещаться в поперечном направлении со скоростью V» называемой скоростью дрейфа. В данных условиях направление и скорость дейст­
вительного перемещения судна относительно воды определяются век­тором V, который является геометрической суммой векторов V_x и V_v (см. рис. 4.3).

Непосредственно из приведенной схемы следует

tga = ~; ^V* • (4.9)

V_x cos а

Для получения формулы угла дрейфа можно воспользоваться первым уравнением системы (4.8) на том основании, что гидродинами­ческая сила R_v согласно (4.7) зависит от угла дрейфа.

Боковая сила руля Р_ру, возникающая в связи с перекладкой руля для удержания судна на курсе, по сравнению с силой R_v при движе­нии с углом дрейфа относительно невелика, поэтому ее в первом при­ближении можно не учитывать и тогда

R.y = Ау,

а после подстановки значений (4.2) и (4.6)

Су Y + - с_а„ -|2- Q„ V. (4.10)

По данным, приведенным в п. 4.1, можно принять значение аэро­динамического коэффициента

Спу= 1,18 sin ^ц). (4.11)

Подстановка в уравнение (4.10) выражений (4.8) и (4.11) при­водит к квадратному уравнению относительно sin а. Решение этого уравнения с последующим переходом от скорости относительно воды V, выраженной в м/с, к скорости по курсу У_л% выраженной в уз

[V _л = —q '§п~ )’ ^и некоторые упрощающие преобразования дают ра­бочую формулу для определения угла дрейфа

|/ (О.ПКл)¹ + ^ —0,\\Vji

tg«- % . (4.12)

^у л

где W — скорость кажущегося ветра, м/с;

Vя — скорость судна по курсу, уз;

к —коэффициент дрейфа, который можно рассчитывать по приближенной форму* ле

*_о-(0.1М-0.в£)|/^Г «'3)

Сопоставление с формулой (4.9) показывает, что числитель фор­мулы (4.12) выражает скорость бокового перемещения судна под вли­янием ветра (скорости дрейфа), а знаменатель — скорость судна по курсу.

Из формулы (4.12) видно, что скорость дрейфа V'_v зависит от ско­рости по курсу V_A: чем больше У_л, тем меньше V_y при тех же значе­ниях W и q_v.

Для практического применения полученной формулы следует учесть еще то обстоятельство, что скорость ветра вблизи поверхности моря за счет трения нижнего слоя воздуха о поверхность воды мень­ше, чем в более высоких слоях. Поскольку измерение скорости ветра анемометром выполняется на высоте мостика, то результаты оказы­ваются несколько завышенными по сравнению со средней скоростью ветра, воздействующего на надводную часть.

Профиль скоростей ветра на высоте подчиняется логарифмиче­скому закону, из которого вытекает, что для получения эквивалент­ного давления скорость ветра, измеренная над верхним мостиком, должна быть умножена на коэффициент 0,83, т. е.

1Р = 0,83Г\ (4.14)

где № —эквивалентная скорость кажущегося ветра для использования в формуле (4.12), м/с;

W' — скорость кажущегося ветра, измеренная анемометром над верхним мостиком, м/с.

Опыт практического использования формулы (4.12) на различ­ных судах показывает, что предвычисление угла дрейфа обеспечива­ется с точностью 1—2°, что примерно соответствует точности графиче­ского счисления пути судна.

Угол дрейфа по формуле (4.12) в условиях плавания легко рас­считывать с помощью калькулятора. При этом следует иметь в виду, что коэффициент дрейфа k_a для каждого конкретного судна зависит только от его осадки, поэтому значения коэффициента целесообразно заранее рассчитать для рабочего диапазона осадок судна с интерва­лом, например, через 1 м и использовать то значение £_а, которое со­ответствует средней осадке на данный период плавания. Переменны­ми величинами будут скорость кажущегося ветра W в м/с, его курсо­вой угол q_w и скорость судна У_л, уз.

Наиболее просто угол дрейфа может быть получен из специаль­ных таблиц дрейфа, рассчитанных по формулам (4.12) с учетом (4.13) и (4.14). Предлагаемые таблицы приведены в прил. 1 и состоят из трех таблиц. Определение угла дрейфа по ним сводится к последо­вательной выборке из трех таблиц (необходимая интерполяция выпол­няется «на глаз»).

Таблицы дрейфа являются универсальными и могут быть исполь­зованы на любом судне по заранее вычисленным значениям k_a для разных осадок.

Влияние переложенного руля на угол дрейфа. При определении уг­ла дрейфа по формуле (4.12), а также с помощью таблиц или номо­граммы, построенных по указанной формуле, не учитывается тот факт, что под действием аэро- и гидродинамической сил, точки приложения которых в общем случае не совпадают с ЦТ судна, последнее имеет тенденцию разворачиваться вокруг вертикальной оси, т. е. приводить­ся к ветру или уваливать в зависимости от знака результирующего момента действующих сил.

Чтобы обеспечить движение заданным курсом, приходится пере­кладывать руль на некоторый средний угол, т. е. создавать момент боковой силы руля для компенсации результирующего момента аэро- и гидродинамической сил. При этом поперечная сила руля P_PV, скла­дываясь алгебраически с поперечной аэродинамической силой А_у, увеличивает или уменьшает скорость бокового перемещения судна V_v% что приводит к изменению угла дрейфа а на величину Да, которая зависит от отношения площадей руля и погруженной части ДП — Sp/S_y.

Для морских транспортных судов можно приблизительно считать, что в среднем

(4.15)

дрешра

V

Рис. 4.4. Силы и моменты» действующие на судно в свободном дрейфе

Учесть влияние перекладки руля на угол дрейфа можно с помощью приближенной формулы, полученной с учетом (4.!5),

Ла°= =F 0,26р. (4.16)

Из приведенной формулы видно, что на каждые 5° перекладки руля угол дрейфа изменяется приблизительно на 1°. При перекладке руля под вегер (судно стремится к ветру) абсолютное значение угла дрейфа уменьшается на величину Ла°. Если же судно уваливает, и приходится руль перекладывать на ветер, то значение угла дрейфа соответственно возрастает.

Дрейф судна с остановленными двигателями. Иногда судну прихо дится длительное время находиться в море с остановленными двигате лями (ожидание светлого времени, неисправность двигателя, ожида­ние распоряжений и т. п.). При наличии ветра судно в данных обсто­ятельствах дрейфует с некоторой скоростью, направление которой в общем случае не совпадает с направлением действующего ветра.

При установившемся дрейфе аэродинамическая сила А уравнове­шивается гидродинамической силой R. Для равновесия судна по курсу необходимо, чтобы аэро- и гидродинамическая силы действовали в од­ной плоскости. При этом условии аэро- и гидродинамический моменты уравновешивают друг друга.

Указанному условию соответствуют положения судна носом или кормой строго против ветра, однако это случаи неустойчивого равно­весия, так как при любом случайном отклонении ДП от данного на­правления возникает поперечная аэродинамическая сила, момент ко­торой стремится развернуть судно еще больше от линии ветра. Одно­временно возникает поперечная гидродинамическая сила, момент ко­торой разворачивает судно в том же направлении, что и аэродинами­ческий момент (рис. 4.4).

Действующие при свободном дрейфе силы и их моменты стремят­ся развернуть судно приблизительно лагом к ветру, следовательно, где-то вблизи этого направления и должно быть положение устойчи­вого равновесия. Данный вывод подтверждается опытом: суда в уста­новившемся свободном дрейфе располагаются примерно лагом к ветру.

Аналитическое определение условий устойчивого свободного дрей­фа выражается системой трех уравнений (1.1), которые для случая ус­тановившегося режима, т. е. при отсутствии инерционных сил, а также равенства нулю силы упора винта и силы на руле, имеют вид:

Rx—^xl |

R_V=A_V; (4.17)

Система (4.17) выражает условие равновесия аэро- и гидродина­мических сил по осям X и К, а также равновесие аэро- и гидродинами­ческого моментов вокруг оси Z.

Продольная гидродинамическая сила R_x выражается зависи­мостью:

= (4.18)

где С_ж —коэффициент продольной гидродинамической силы, который для движения с углом дреАфа может быть получен по эмпирической формуле

С, = 0,075 sin ^168»^ <^4Л9>

Продольная аэродинамическая сила А_х выражается приближен­ной формулой:

А* ~ 1.3-Ё²-<?«*’* cos V»-. (4.20)

где Qx — лобовая площадь парусности, м².

Ранее были приведены формулы для выражения поперечных сил и их коэффициентов: (4.2), (4.6), (4.7) и (4.11).

Условие равновесия одновременно по осям X и У можно получить, если поделить второе уравнение на первое системы (4.17):

4^L- ^{(4 2|)}

Дат Л*

Подставляя в найденное условие выражения (4.2), (4.6), (4.18) и (4.20), окончательно получим

. _________________ 0,23 sin a-f 1,09 sin» а Q_x

(*.,«-Т_Т) 0.075S.*

Полученное выражение дает возможность для любого значения угла дрейфа а определить значение курсового угла ветра q_Wt при ко­тором обеспечивается равновесие сил по продольной и поперечной осям одновременно. I

Второе условие устойчивого свободного дрейфа выражается рав­новесием аэро- и гидродинамического моментов относительно верти­кальной оси, проходящей через ЦТ судна.

Если разделить третье уравнение на второе системы (4.17), то, учитывая, что отношение момента к силе равняется плечу этой силы, получим указанное условие в виде равенства плеч аэро- и гидроди­намической сил

(4.23)

Рис. 4.5. Положение судна при свободном дрейфе в зависимости от знака смещения ЦП от ЦТ:

а — ЦП смещен в нос от ЦТ; б — ЦП смешен в корму от ЦТ

Подставляя значения плеч из формул (4.3) и (4.4) и учитывая при этом, что ЦБС располагается, как правило, достаточно близко к ЦТ судна (/_ЦБС « 0), получим окончательно второе условие равно­весия при свободном дрейфе

,; = 2(«° -45° + 1807_ц„). (4.24)

Положение устойчивого равновесия при дрейфе с остановленными двигателями будет иметь место при одновременном выполнении двух условий, выражаемых формулами (4.22) и (4.24).

На большинстве морских судов коэффициент ft находится в пре­делах 0,6—0,8, а отношение d)L — в пределах 0,03—0,07, поэтому мож­но приближенно принять средние постоянные значения:

6- 0,7; d/L=0,5.

С учетом принятых значений по формулам (4.22) и (4.24) по­строена номограмма для определения q°_w и а° по Q_VIQ_X и 7ц„, приве­денная в прил. 2.

Номограмма показывает, что при больших значениях 7_ЦП направ­ление свободного дрейфа может существенно отличаться от направле­ния ветра (порядка до 20°), что следует учитывать на практике.

Положения судна при свободном дрейфе в зависимости от знака 7_ЦП и действующей силы показаны на рис. 4.5.

При свободном дрейфе практически важно знать не только на­правление движения, но и скорость судна относительно воды V.

Из приведенной схемы (см. рис. 4.5) видно, что

у_ ^V* _ ^ (4 251

cos (90°— a⁰) sin а *

где v_v — поперечная составляющая скорости судна.

Поперечная составляющая скорости V_v соответствует скорости дрейфа «на стопе» К_в0, которую можно получить по таблицам дрей­фа (см. прил. 1).

4.3. Маневрирование в условиях ветра

При маневрировании в условиях ветра внешние силы и их мо­менты, особенно при небольших скоростях движения, сопоставимы с силами и моментами средств управления (руля и винта), а нередко и превосходят их, что затрудняет или делает даже невозможным вы­полнение того или иного маневра из-за резкого ухудшения или потери управляемости.

Для оценки и прогнозирования поведения судна при маневриро­вании в условиях ветра воспользуемся уже известными нам обшими закономерностями отдельно для аэро- и гидродинамических сил и их моментов.

На рис. 4.6 схематически показано действие на судно аэро- и гид­родинамических сил в зависимости от курсового угла кажущегося вет­ра для трех условий.

Точки приложения поперечных сил показаны в соответствии с приближенными формулами (4.3) и (4.4) для плеч аэро- и гидродина­мической сил соответственно. При этом для простоты сделано допуще­ние, что ЦП и ЦТ совпадают по длине судна и находятся в точке G (такое допущение достаточно справедливо для судов без дифферента с надстройкой, расположенной посредине, а также для судов с кор­мовым расположением надстройки, но имеющих такой дифферент ^на корму, при котором ЦП смещен вперед до совпадения с ЦТ судна).

Рассмотрим подробнее каждый из трех случаев (см. рис. 4.6).

Ветер со стороны носовых курсовых углов. Поток воздуха, дейст­вующий на надводную часть судна, имеющего скорость v_x> со стороны носового курсового угла (см. рис. 4.6, а) создает поперечную аэроди­намическую силу А_у. Точка ее приложения в соответствии с формулой

(4.3) смещена от ЦТ вперед по ДП, т. е. навстречу потоку воздуха, на расстояние 1л. В связи с этим создается момент А_у1_а, стремящийся развернуть судно в направлении увеличения q_u-_% т. е. носом от ветра. В то же время сила А_и создает поперечное движение со скоростью