Упрощение математических моделей

После перехода от описания моделируемой системы S к ее модели M_к, построенной по блочному принципу, необходимо построить математические модели процессов, происходящих в различных блоках. Математическая модель представляет собой совокупность соотношений (например, уравнений, логических условий, операторов), определяющих характеристики процесса функционирования системы S в зависимости от структуры системы, алгоритмов поведения, параметров системы, воздействий внешней среды E, начальных условий и времени. Математическая модель является результатом формализации процесса функционирования исследуемой системы, т.е. построения формального (математического) описания процесса с необходимой в рамках проводимого исследования степенью приближения к действительности.

Для иллюстрации возможностей формализации рассмотрим процесс функционирования некоторой гипотетической системы S, которую можно разбить на m подсистем с характеристиками y₁ (t), y₂ (t), …, y_hy (t) с параметрами h₁, h₂, …, h_nH при наличии входных воздействий x₁, x₂, …, x_nX и воздействий внешней среды 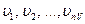. Тогда математической моделью процесса может служить система соотношений вида

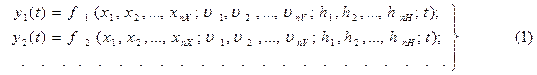
Если бы функции f₁, f₂, …, f_m были известны, то соотношения (1) оказались бы идеальной математической моделью процесса функционирования системы S. Однако на практике получение модели достаточно простого вида для больших систем чаще всего невозможно, поэтому обычно процесс функционирования системы S разбивают на ряд элементарных подпроцессов. При этом необходимо так проводить разбиение на подпроцессы, чтобы построение моделей отдельных подпроцессов было элементарно и не вызывало трудностей при формализации. Таким образом, на этой стадии сущность формализации подпроцессов будет состоять в подборе типовых математических схем. Например, для стохастических процессов это могут быть схемы вероятностных автоматов (P-схемы), схемы массового обслуживания (Q-схемы) и т.д., которые достаточно точно описывают основные особенности реальных явлений, составляющих подпроцессы, с точки зрения решаемых прикладных задач.

Таким образом, формализация процесса функционирования любой системы S должно предшествовать изучение составляющих его явлений. В результате появляется содержательное описание процесса, которое представляет собой первую попытку четко изложить закономерности, характерные для исследуемого процесса, и постановку прикладной задачи. Содержательное описание является исходным материалом для последующих этапов формализации: построения формализованной схемы процесса функционирования системы и математической модели этого процесса. Для моделирования процесса функционирования системы на ЭВМ необходимо преобразовать математическую модель процесса в соответствующий моделирующий алгоритм и машинную программу.

Подэтапы первого этапа моделирования. Рассмотрим более подробно основные подэтапы построения концептуальной модели системы M_к и ее формализации.

1.1. Постановка задачи машинного моделирования системы. Дается четкая формулировка задачи исследования конкретной системы S и основное внимание уделяется таким вопросам, как: а) признание существования задачи и необходимости машинного моделирования; б) выбор методики решения задачи с учетом имеющихся ресурсов; в) определение масштаба задачи и возможности разбиения ее на подзадачи.

Необходимо также ответить на вопрос о приоритетности решения различных подзадач, оценить эффективность возможных математических методов и программно-технических средств их решения. Тщательная проработка этих вопросов позволяет сформулировать задачу исследования и приступить к ее реализации. При этом возможен пересмотр начальной постановки задачи в процессе моделирования.

1.2. Анализ задачи моделирования системы. Проведение анализа задачи способствует преодолению возникающих в дальнейшем трудностей при ее решении методом моделирования. На рассматриваемом втором этапе основная работа сводится именно к проведению анализа, включая: а) выбор критериев оценки эффективности процесса функционирования системы S; б) определение эндогенных и экзогенных переменных модели M; в) выбор возможных методов идентификации; г) выполнение предварительного анализа содержания второго этапа алгоритмизации модели системы и ее машинной реализации; д)выполнение предварительного анализа содержания третьего этапа получения и интерпретации результатов моделирования системы.

1.3. Определение требований к исходной информации об объекте моделирования и организация ее сбора. После постановки задачи моделирования системы S определяются требования к информации, из которой получают качественные и количественные исходные данные, необходимые для решения этой задачи. Эти данные помогают глубоко разобраться в сущности задачи, методах ее решения. Таким образом, на этом подэтапе проводится: а) выбор необходимой информации о системе S и внешней среде E; б) подготовка априорных данных; в) анализ имеющихся экспериментальных данных; г) выбор методов и средств предварительной обработки информации о системе.

При этом необходимо помнить, что именно от качества исходной информации об объекте моделирования существенно зависят как адекватность модели, так и достоверность результатов моделирования.

1.4. Выдвижение гипотез и принятие предположений. Гипотезы при построении модели системы S служат для заполнения «пробелов» и понимания задачи исследователем. Выдвигаются такие гипотезы относительно возможных результатов моделирования системы S, справедливость которых проверяется при проведении машинного эксперимента. Предположения предусматривают, что некоторые данные известны или их нельзя получить. Предположения могут выдвигаться относительно известных данных, которые не отвечают требованиям решения поставленной задачи. Предположения дают возможность провести упрощения модели в соответствии с выбранным уровнем моделирования. При выдвижении гипотез и принятия предположений учитываются следующие факторы: а) объем имеющейся информации для решения задач; б) подзадачи, для которых информация недостаточна; в) ограничения на ресурсы времени для решения задачи; г) ожидаемые результаты моделирования.

Таким образом, в процессе работы с моделью системы S возможно многократное возвращение к этому подэтапу в зависимости от полученных результатов моделирования и новой информации об объекте.

1.5. Определение параметров и переменных модели. Прежде чем перейти к описанию математической модели, необходимо определить параметры системы 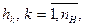входные и выходные переменные 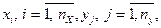воздействия внешней среды 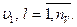Конечной целью этого подэтапа является подготовка к построению математической модели системы S, функционирующей во внешней среде E, для чего необходимо рассмотрение всех параметров и переменных модели и оценка степени их влияния на процесс функционирования системы в целом. Описание каждого параметра и переменной должно даваться в следующей форме: а) определение и краткая характеристика; б) символ обозначения и единица измерения; в) диапазон изменения; г) место применения в модели.

1.6. Установление основного содержания модели. На этом подэтапе определяется основное содержание модели и выбирается метод построения модели системы, которые разрабатываются на основе принятых гипотез и предположений. При этом учитываются следующие особенности: а) формулировка задачи моделирования системы; б) структура системы S и алгоритмы ее поведения, воздействия внешней среды E; в) возможные методы и средства решения задачи моделирования.

1.7. Обоснование критериев оценки эффективности системы. Для оценки качества процесса функционирования моделируемой системы S необходимо выбрать некоторую совокупность критериев оценки эффективности, т.е. в математической постановке задача сводится к получению соотношения для оценки эффективности как функции параметров и переменных системы. Эта функция представляет собой поверхность отклика в исследуемой области изменения параметров и переменных и позволяет определить реакцию системы. Эффективность системы S можно оценить с помощью интегральных или частных критериев, выбор которых зависит от рассматриваемой задачи.

1.8. Определение процедур аппроксимации. Для аппроксимации реальных процессов, протекающих в системе S, обычно используются три вида процедур: а) детерминированную; б) вероятностную; в) определения средних значений.

При детерминированной процедуре результаты моделирования однозначно определяются по данной совокупности входных воздействий, параметров и переменных системы S. В этом случае отсутствуют случайные элементы, влияющие на результаты моделирования. Вероятностная (рандомизированная) процедура применяется в том случае, когда случайные элементы, включая воздействия внешней среды E, влияют на характеристики процесса функционирования системы S и когда необходимо получить информацию о законах распределения выходных переменных. Процедура определения средних значений используется тогда, когда при моделировании системы интерес представляют средние значения выходных переменных при наличии случайных элементов.

1.9. Описание концептуальной модели системы. На этом подэтапе построения модели системы: а) описывается концептуальная модель M_к в абстрактных терминах и понятиях; б) дается описание модели с использованием типовых математических схем; в)принимаются окончательно гипотезы и предположения; г) обосновывается выбор процедуры аппроксимации реавльных процессов при построении модели. Таким образом, на этом подэтапе проводится пробный анализ задачи, рассматриваются возможные методы ее решения и дается детальное описание концептуальной модели M_к, которая затем используется на втором этапе моделирования.

1.10. Проверка достоверности концептуальной модели. После того как концептуальная модель M_к описана, необходимо проверить достоверность некоторых концепций модели перед тем, как перейти к следующему этапу моделирования системы S. Проверять достоверность концептуальной модели достаточно сложно, так как процесс ее построения является эвристическим и такая модель описывается в абстрактных терминах и понятиях. Один из методов проверки модели M_к -применение операций обратного перехода, позволяющий проанализировать модель, вернуться к принятым аппроксимациям и, наконец, рассмотреть снова реальные процессы, протекающие в моделируемой системе S. Проверка достоверности концептуальной модели M_к должна включать: а) проверку замысла модели; б0 оценку достоверности исходной информации; в) рассмотрение постановки задачи моделирования; г) анализ принятых аппроксимаций; д) исследование гипотез и предположений.

Только после тщательной проверки концептуальной модели M_к не позволяют получить достоверные результаты моделирования.

2.Качественный анализ уровня адекватности моделей

Проверка достоверности модели системы. Эта проверка является первой из проверок, выполняемых на этапе реализации модели. Так как модель представляет собой приближенное описание процесса функционирования реальной системы S, то до тех пор, пока не доказана достоверность модели M_м, нельзя утверждать, что с ее помощью будут получены результаты, совпадающие с теми, которые могли бы быть получены при проведении натурного эксперимента с реальной системой S. Поэтому определение достоверности модели можно считать наиболее важной проблемой при моделировании систем. От решения этой проблемы зависит степень доверия к результатам, полученным методом моделирования. Проверка модели на рассматриваемом подэтапе должна дать ответ на вопрос, насколько логическая схема модели системы и используемые математические соотношения отражают замысел модели, сформированный на первом этапе. При этом проверяются: а) возможность решения поставленной задачи; б) точность отражения замысла в логической схеме; в) полнота логической схемы модели; г) правильность используемых математических соотношений.

Только после того, как разработчик убеждается путем соответствующей проверки в правильности всех этих положений, можно считать, что имеется логическая схема модели системы S, пригодная для дальнейшей работы по реализации модели на ЭВМ.

При реализации моделирующих алгоритмов на ЭВМ вырабатывается информация о состояниях процесса функционирования исследуемых систем z (t) є Z. Эта информация является исходным материалом для определения приближенных оценок искомых характеристик, получаемых в результате машинного эксперимента, т.е. критериев оценки. Критерием оценки будем называть любой количественный показатель, по которому можно судить о результатах моделирования системы. Критериями оценки могут служить показатели, получаемые на основе процессов, действительно протекающих в системе или получаемых на основе специально сформированных функций этих процессов.

В ходе машинного эксперимента изучается поведение исследуемой модели M процесса функционирования системы S на заданном интервале времени [О,Т].Поэтому критерий оценки является в общем случае векторной случайной функцией, заданной на этом же интервале:

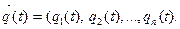
Часто используют более простые критерии оценки, например, вероятность определенного состояния системы в заданный момент времени t * є [О, Т], отсутствие отказов и сбоев в системе на интервале [О,Т] и т.д. При интерпретации результатов моделирования вычисляются различные статистические характеристики закона распределения критерия оценки.

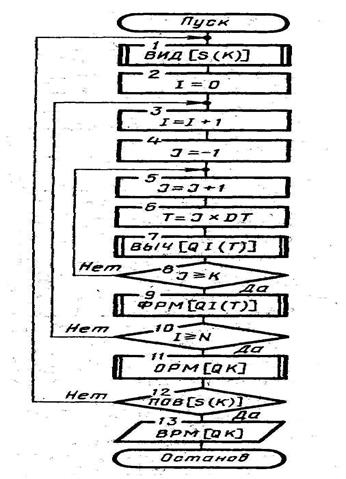
Рассмотрим общую схему фиксации и обработки результатов моделирования системы, которая приведена на рис. 3. Будем рассматривать гипотетическую модель M, предназначенную для исследования поведения системы S на интервале времени [О, Т]. В общем случае критерием интерпретации результатов моделирования является нестационарный случайный n-мерный процесс 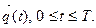Полагаем для определенности, что состояние моделируемой системы S проверяется каждые Δ t временных единиц, т.е. используется «принцип Δ t». При этом вычисляют значения 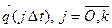, критерия 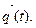Таким образом, о свойствах случайного процесса 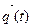судят по свойствам случайной последовательности 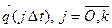, или, иначе говоря, по свойствам m-мерного вектора вида

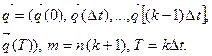
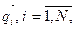Процесс функционирования системы S на интервале [О, Т] моделируется N-кратно с получением независимых реализаций вектора 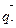Работа модели на интервале [О, Т] называется прогоном модели.

На схеме, изображенной на рис. 3, обозначено I≡i; J≡j; K≡k; N≡N; T≡t; DT≡Δt; Q≡q.

В общем случае алгоритмы фиксации и статистической обработки данных моделирования содержат три цикла. Полагаем, что имеется машинная модель M_м системы S.

В н у т р е н и й ц и к л (блоки 5-8), позволяет получить последо-вательность 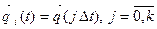в моменты времени t=0, Δ t, 2 Δ t, …, k Δ t=T.

Рис.3.

Основной блок 7 реализует процедуру вычисления последовательности 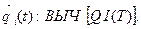Именно в этом блоке имитируется процесс функционирования моделируемой системы S на интервале времени [О, Т].

П р о м е ж у т о ч н ы й ц и к л (блоки 3-10), в котором организуется N-кратное повторение прогона модели, позволяющее после соответствующей статистической обработки результатов судить об оценках характеристик моделируемого варианта системы. Окончательное моделирование варианта системы S может определяться не только заданным числом реализаций (блок 10), как это показано на схеме, но и заданной точностью результатов моделирования. В этом цикле содержится блок 9, реализующий процедуру фиксации результатов моделирования по i-му прогону модели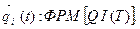

В н е ш н и й ц и к л (блоки 1-12) охватывает оба предшествующих цикла и дополнительно включает блоки 1, 2, 11, 12, управляющие последовательностью моделирования вариантов системы S. Здесь организуется поиск оптимальных структур, алгоритмов и параметров системы S, т.е. блок 11 обрабатывает результаты моделирования исследуемого k–го варианта системы OPM [Q, K], блок 12 проверяет удовлетворительность полученных оценок характеристик процесса функционирования системы 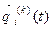требуемым (ведет поиск оптимального варианта системы ПОВ [S (K)], блок 1 изменяет структуру, алгоритмы и параметры системы S на уровне ввода исходных данных для очередного k–го варианта системы ВИД [S (K)]. Блок 13 реализует функцию выдачи результатов моделирования по каждому k–му варианту модели системы S_k^, т.е. ВРМ [Q K].

Рассмотренная схема позволяет вести статистическую обработку результатов моделирования в наиболее общем случае при нестационарном критерии 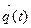. В частных случаях можно ограничиться более простыми схемами.

Если свойства моделируемой системы S определяются значением критерия 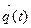в некоторый заданный момент времени, например в конце периода функционирования модели t=kΔ t=T, то обработка сводится к оценке распределения n-мерного вектора 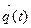по независимым реализациям 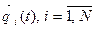, полученным в результате N прогонов модели.

Если в моделируемой системе S по истечению некоторого времени с начала работы t₀=k₀Δ t установится стационарный режим, то о нем можно судить по одной, достаточно длинной реализации 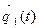критерия 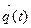, стационарного и эргодического на интервале [t₀, Т]. Для рассмотренной схемы это означает, что исключается средний цикл (n=1) и добавляется оператор, позволяющий начать обработку значений 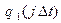при j≥k₀.

Другая особенность применяемых на практике методов статистической обработки результатов моделирования связана с исследованием процесса функционирования систем с помощью моделей блочной конструкции. В этом случае часто приходится применять раздельное моделирование отдельных блоков модели, когда имитация входных воздействий для одного блока проводится на основе оценок критериев, полученных предварительно на другом блоке модели. При раздельном моделировании может иметь место либо непосредственная запись в накопителе реализаций критериев, либо их аппроксимация, полученная на основе статистической обработки результатов моделирования с последующим использованием генераторов случайных чисел для имитации этих воздействий.