ЛЕКЦИЯ 13. Идентификация нелинейных динамических объектов

1. Применение гармонической линеаризации при идентификации объектов.

2. Использование метода статистической линеаризации для идентификации нелинейных объектов

3. Идентификация нелинейных объектов с использованием функциональных степенных рядов

1. В инженерной практике большое применение находят приближенные методы, основанные на замене действительных зависимости между входной и выходной переменными приближенными линейными. При этом линеаризацию необходимо производить так, чтобы учесть хотя бы приближенно нелинейные свойства звеньев, т.е. чтобы для линеаризованных элементов не выполняется принцип суперпозиции.

Линеаризация нелинейных характеристик путем разложения в рядсостоит в замене характеристики у = f(x) приближенной линейной зависимостью, определяемой двумя первыми членами разложения характеристики в ряд Тейлора . Пусть характеристика у = f(x) дифференцируема и входной сигнал х (f) мало отличается от некоторого среднего значения х₀, тогда зависимость у = f(x) можно заменить приближенной

у = f(x₀) + f ' (х-₀) (х - х₀). (2.131)

Замена нелинейной зависимости у =f(x) линейной геометрически представляет собой замену кривой у= f(x), касательной к ней в точке х₀.

Действующие внешние возмущения можно представить как стационарные случайные функции х (г) с математическим ожиданием т_х и центрированной случайной составляющей л(г):

x(t)^m_x + x(t). (2.132)

В этом случае практически линеаризацию нелинейной характеристики целесообразно производить относительно центрированного входного случайного сигнала x(t), т.е. за центр разложения .х₀ в (2.131) взять математическое ожидание т_х входного сигнала х(1). В результате получается

у (г) *./>У + ./' (т_х) х (г). (2.13.3)

Таким образом, приближенная зависимость (2.133) линейна только относительно случайной составляющей x(t) входного сигнала и нелинейно относительно математического ожидания т_х, поэтому принцип суперпозиции здесь неприменим.

Гармоническая линеаризация.В целом ряде практических задач приходится рассматривать воздействие на линейное звено гармонических колебаний

X(t)= A sin ωt = A sin ψ, ψ=ωt.

Выходной сигнал нелинейного звена также будем периодическим, но не гармоническим.

Идея гармонической линеаризации состоит в том, что выходные периодические колебания у(t) разлагают в ряд Фурье и для дальнейших исследований ограничиваются рассмотрением лишь первых гармоник этого ряда. В этом случае нелинейная зависимость у= у(t)=f(Asinψ) заменяется приближенной

Y(t)=a₀+asin ωt+bcosωt=a₀+ q₁x+q₂x/ω,

где

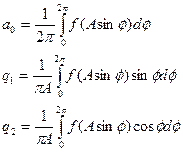
Статистическая линеаризация. Метод приближенной замены нелинейной характеристики эквивалентными в вероятностном смысле линейными зависимостями называется методом статистической линеаризации. В результате такой линеаризации нелинейная зависимость у=f(t) заменяется приближенной

y(t)=k_am_x + k,x⁰(t).

где m_x = const — математическое ожидание стационарного случайного сигнала на входе нелинейного элемента; x⁰(t) — центрированная случайная составляющая входного сигнала х (t).

Предполагается, что выходной стационарный случайный сигнал может быть представлен в виде

у(t) = т_у. + у^/(t)

где т_у — математическое ожидание у(t); y^/(t) -центрированная случайная составляющая y(t). Коэффициент

к₀ = т_у/т_х

называется статистическим коэффициентом усиления нелинейного звена по математическому ожиданию. Коэффициент

k₁=±σ_y/ σ _x .

3. Идентификация нелинейных объектов с использованием функциональных степенных рядов

Производная функции определяется разностным отношением:

.

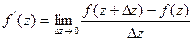Если существует предел и не зависит от того, как стремится к нулю, то функция является аналитической. Следовательно в окрестности некоторой точки а можно ее разложить в ряд Тейлора:

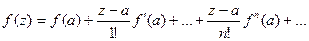
Если а=0 , то получаем ряд Маклорена:

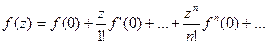
Учитывая , что последующие слагаемые выше второго достаточно малые величины, можно заменить функцию линейной частью разложения.