Показники безвідмовності
Імовірність безвідмовної роботи – імовірність того, що протягом заданого наробітку відмова об’єкта не виникне.
Імовірність безвідмовної роботи об’єкта характеризує можливість виконання ним заданих функцій за певний час t і визначається як імовірність того, що тривалість його безвідмовної роботи T (наробіток до відмови) буде не менша часу t:

Імовірність безвідмовної роботи пов’язана з функцією розподілу наробітку до відмови F(t) таким чином:
P(t) = 1 – F(t). (2.2)
Як і будь–яка ймовірність, імовірність безвідмовної роботи змінюється від 1 до 0 (при t = 0 вона дорівнює 1, при t = ¥ дорівнює 0).
Імовірність безвідмовної роботи за інтервал часу від 0 до t визначається при статистичних випробовуваннях як відношення кількості працездатних об’єктів у момент часу t до кількості об’єктів, які поставлено на випробовування (тобто до кількості працездатних об’єктів у початковий момент часу t = 0):

де N 0 – кількість об’єктів, які поставлено на випробування (за умовою, що об’єкти, які відмовили, не замінюються і не відновлюються);
n(t) – кількість об’єктів, що відмовили на інтервалі часу 0 – t.
Імовірність відмови – імовірність того, що протягом заданого наробітку виникне відмова об’єкта.
Імовірність відмови об’єкта визначається як імовірність того, що тривалість його безвідмовної роботи T (наробіток до відмови) буде менша часу t:

Імовірність відмови визначають для заданого наробітку (визначеного інтервалу часу) за формулою
Q(t) = F(t)= 1 – Р (t). (2.5)
Імовірність відмови та імовірність безвідмовної роботи події протилежні й у сумі дають одиницю, тобто
Q(t) +Р (t) = 1. (2.6)
Статистичне визначення ймовірності відмови – це відношення кількості об’єктів, що відмовили на інтервалі часу 0 – t,до кількості об’єктів, які поставлено на випробовування:

Значення Р(t) і Q(t) не мають сенсу без указівки часу t.
Щільність розподілу наробітку до відмови (закон розподілу відмов) – щільність імовірності відмови до моменту часу t, або щільність імовірності того, що тривалість роботи об’єкта до відмови буде менше t.
Імовірність безвідмовної роботи та ймовірність відмови пов’язана з щільністю розподілу наробітку до відмови f(t) таким чином:
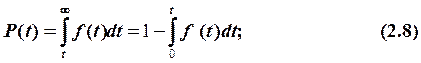
 |
Або, після диференціювання,


Тобто
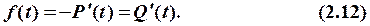
Статистичне визначення щільності розподілу наробітку до відмови:

Інтенсивність відмов– умовна щільність імовірності виникнення відмови невідновного об’єкта, яка визначається за умови, що до цього моменту відмова не виникла.
Визначається за формулою

або

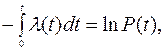 |
Проінтегруємо вираз (2.15) від 0 до t:
звідки

Формула (2.16) зв’язує ймовірність безвідмовної роботи об’єктів з інтенсивністю їх відмов для будь–якого закону зміни інтенсивності у часі (закону розподілу відмов).
Статистичне визначення інтенсивності відмов:

де Nср – середня кількість об’єктів, які працювали безвідмовно на інтервалі часу D t:
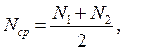
де N1, N2 – кількість об’єктів, які працювали безвідмовно відповідно до початку і до кінця інтервалу часу D t.
Інтенсивність відмов є показником безвідмовності неремонтуємих і невідновлюваних об’єктів.
Наробіток– тривалість чи обсяг роботи.
Наробіток може бути як неперервною величиною (тривалість роботи у годинах, кілометрах пробігу тощо), так і цілочисельною величиною (кількість робочих циклів, спрацьовувань тощо).
Наробіток до відмови –наробіток об’єкта від початку його експлуатації до виникнення першої відмови.
 |
Середній наробіток до відмови –математичне сподівання наробітку об’єкта до першої відмови.
де t – наробіток до відмови;
Р (t) – імовірність безвідмовної роботи (функція безвідмовності).
 |
Статистичне визначення cереднього наробітку до відмови:
де ti – наробіток до відмови і-об’єкта.
Наробіток між відмовами– наробіток об’єкта від завершення відновлення його працездатного стану після відмови до виникнення наступної відмови.
Середній наробіток на відмову (середній наробіток між відмовами)– відношення сумарного наробітку відновного об’єкта до математичного сподівання кількості його відмов протягом цього наробітку
 |
Статистична оцінка середнього наробітку на відмову:
де tоі – наробіток відновного об’єкта між двома його сусідніми відмовами, тобто від початку його функціонування або відновлення до моменту наступної відмови;
n –кількість відмов одного відновного об’єкта.
 |
Якщо випробовують N однотипних зразків, тоді середній наробіток на відмову визначають за формулою
де tсі – середній наробіток між відмовами і - зразка.
Параметр потоку відмов – відношення математичного сподівання кількості відмов відновного об’єкта за досить малий його наробіток до значення цього наробітку.
Для визначення статистичної оцінки параметра потоку відмов використовують формулу

де N0 – кількість об’єктів, які поставлено на випробування (об’єкти, що відмовили, замінюються на нові).
Дата добавления: 2016-06-13; просмотров: 2608;
