Функции FIRST и FOLLOW
При построении таблицы предсказывающего анализатора нам потребуются две функции - FIRST и FOLLOW.
Пусть G = (N, T, P, S) - КС-грамматика. Для  - произвольной цепочки, состоящей из символов грамматики, определим
- произвольной цепочки, состоящей из символов грамматики, определим 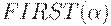 как множество терминалов, с которых
как множество терминалов, с которых
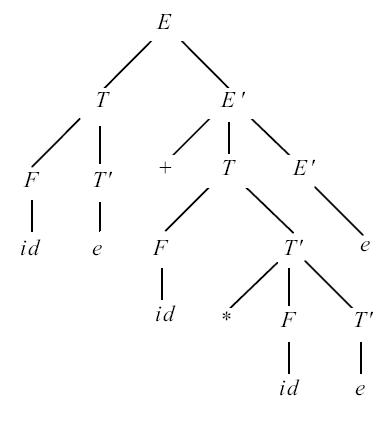
Рис. 4.3.
начинаются строки, выводимые из  Если
Если 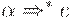 , то e также принадлежит
, то e также принадлежит 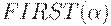 .
.
Определим FOLLOW(A) для нетерминала A как множество терминалов a, которые могут появиться непосредственно справа отA в некоторой сентенциальной форме грамматики, то есть множество терминалов a таких, что существует вывод вида 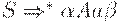 для некоторых
для некоторых 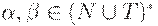 . Заметим, что между A и a в процессе вывода могут находиться нетерминальные символы, из которых выводится e. Если A может быть самым правым символом некоторой сентенциальной формы, то $ также принадлежит FOLLOW(A).
. Заметим, что между A и a в процессе вывода могут находиться нетерминальные символы, из которых выводится e. Если A может быть самым правым символом некоторой сентенциальной формы, то $ также принадлежит FOLLOW(A).
Рассмотрим алгоритмы вычисления функции FIRST.
Алгоритм 4.3. Вычисление FIRST для символов КС- грамматики.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Множество FIRST(X) для каждого символа  .
.
Метод. Выполнить шаги 1-3:
(1) Если X - терминал, то положить FIRST(X) = {X}; если X - нетерминал, положить 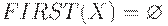 .
.
(2) Если в P имеется правило X -> e, то добавить e к FIRST(X).
(3) Пока ни к какому множеству FIRST(X) нельзя уже будет добавить новые элементы, выполнять:
do { continue = false; Для каждого нетерминала X Для каждого правила X -> Y1Y2...Yk {i=1; nonstop = true; while (i <= k && nonstop) {добавить FIRST(Yi) n {e} к FIRST(X); if (Были добавлены новые элементы) continue = true; if (e != FIRST (Yi)) nonstop = false; else i+ = 1; } if (nonstop) {добавить e к FIRST(X); continue = true; } } }while (continue);Алгоритм 4.4. Вычисление FIRST для цепочки.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Множество 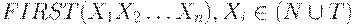 .
.
Метод. Выполнить шаги 1-3:
(1) При помощи алгоритма 4.3. вычислить FIRST(X) для каждого  .
.
(2) Положить 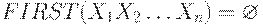 .
.
(3)
{i = 1; nonstop = true; while (i <= && nonstop) {добавить FIRST(Xi) n {e} к FIRST(u); if (e not in FIRST(Xi) nonstop = false; else i+ = 1; }if (nonstop) {добавить e к FIRST(u); } }Рассмотрим алгоритм вычисления функции FOLLOW.
Алгоритм 4.5. Вычисление FOLLOW для нетерминалов грамматики.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Множество FOLLOW(X) для каждого символа 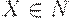 .
.
Метод. Выполнить шаги 1-4:
(1) Положить  для каждого символа
для каждого символа 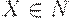 .
.
(2) Добавить $ к FOLLOW(S).
(3) Если в P eсть правило вывода  , где
, где 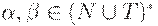 , то все элементы из
, то все элементы из  , за исключением e, добавить к FOLLOW(B).
, за исключением e, добавить к FOLLOW(B).
(4) Пока ничего нельзя будет добавить ни к какому множеству FOLLOW(X), выполнять:
если в P есть правило  или
или  ,
, 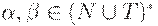 , где
, где  содержит
содержит 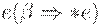 , то все элементы из FOLLOW(A) добавить к FOLLOW(B).
, то все элементы из FOLLOW(A) добавить к FOLLOW(B).
Пример 4.4. Рассмотрим грамматику из примера 4.3. Для нее
FIRST(E) = FIRST(T) = FIRST(F) = {(, id}FIRST(E') = {+, e}FIRST(T') = {*, e}FOLLOW(E) = FOLLOW(E') = { ), $}FOLLOW(T) = FOLLOW(T') = {+, ), $}FOLLOW(F) = {+, *, ), $}Например, id и левая скобка добавляются к FIRST(F) на шаге 3 при i = 1, поскольку FIRST(id) = {id} и FIRST("(") = {"("} в соответствии с шагом 1. На шаге 3 при i = 1, в соответствии с правилом вывода T -> FT', к FIRST(T) добавляются такжеid и левая скобка. На шаге 2 в FIRST(E') включается e.
Также при вычислении множеств FOLLOW на шаге 2 в FOLLOW(E) включается $. На шаге 3, на основании правила F -> (E), кFOLLOW(E) добавляется также правая скобка. На шаге 4, примененном к правилу E -> TE', в FOLLOW(E') включаются $ и правая скобка. Поскольку 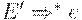 , они также попадают и во множество FOLLOW(T). В соответствии с правилом вывода E -> TE', на шаге 3 в FOLLOW(T) включаются и все элементы из FIRST(E'), отличные от e.
, они также попадают и во множество FOLLOW(T). В соответствии с правилом вывода E -> TE', на шаге 3 в FOLLOW(T) включаются и все элементы из FIRST(E'), отличные от e.
Определим теперь функцию FIRSTk(R), где k - натуральное число и 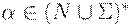 .
.
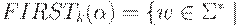 либо |w| < k и
либо |w| < k и 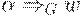 , либо
, либо 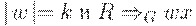 для некоторого
для некоторого  .
.
Если  , то
, то  , где w - это первые k символов цепочки
, где w - это первые k символов цепочки  при
при  и
и  при
при  .
.
Приведем алгоритм вычисления функции 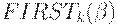 , где
, где 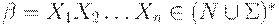 .
.
Определение. Пусть 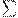 - некоторый алфавит. Если L1 и L2 - подмножества
- некоторый алфавит. Если L1 и L2 - подмножества  , то положим
, то положим

Лемма 4.1. Для любой КС-грамматики 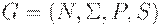 и любых
и любых 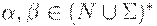

Доказательство оставляем читателю в качестве упражнения.
Aлгоритм 4.6. Вычисление функции  .
.
Вход. КС-грамматика 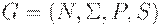 и цепочка
и цепочка 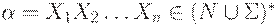 .
.
Выход. 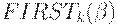 .
.
Метод.Так как по последней лемме
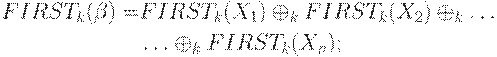
то достаточно показать, как найти FIRSTk(X) для 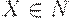 .
.
Если 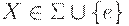 , то очевидно, что FIRSTk(X) = {X}.
, то очевидно, что FIRSTk(X) = {X}.
Определим множества Fi(X) для каждого  и возрастающих значений i >= 0:
и возрастающих значений i >= 0:
(1) Fi(a) = {a} для всех 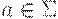 и i >= 0:
и i >= 0:
(2)  и существует правило
и существует правило 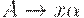 из P, для которого либо |x| = k, либо |x| < k и
из P, для которого либо |x| = k, либо |x| < k и  .
.
(3) Допустим, что F0, F1..., Fi-1 уже определены для всех  . Тогда
. Тогда
 принадлежит P и
принадлежит P и 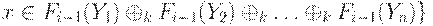
(4) Так как 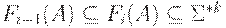 для всех A и i, то в конце концов мы дойдем до такого i, что Fi-1(A) = Fi(A) для всех
для всех A и i, то в конце концов мы дойдем до такого i, что Fi-1(A) = Fi(A) для всех  . Тогда положим FIRSTk(A) = Fi(A) для этого значения i.
. Тогда положим FIRSTk(A) = Fi(A) для этого значения i.
Дата добавления: 2016-06-13; просмотров: 3312;
