Конструирование LR(1)-таблицы

Рассмотрим алгоритм конструирования таблицы, управляющей LR(1) - анализатором.

Пусть G = (N, T, P, S) - КС-грамматика. Пополненной грамматикой для данной грамматики G называется КС- Состояния Action Goto

Рис. 4.7.

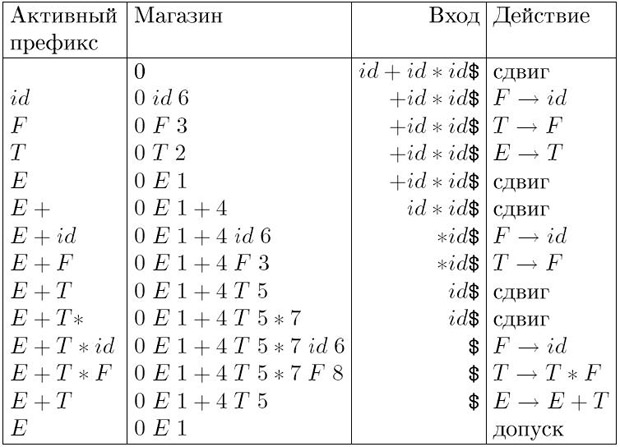
Рис. 4.8.

грамматика

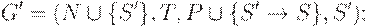
то есть эквивалентная грамматика, в которой введен новый начальный символ S' и новое правило вывода S' -> S.

Это дополнительное правило вводится для того, чтобы определить, когда анализатор должен остановить разбор и зафиксировать допуск входа. Таким образом, допуск имеет место тогда и только тогда, когда анализатор готов осуществить свертку по правилу S' -> S.

LR(1)- ситуацией называется пара 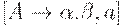, где - правило грамматики, a - терминал или правый концевой маркер $. Вторая компонента ситуации называется аванцепочкой.

Будем говорить, что LR(1)-ситуация 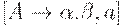допустима для активного префикса +, если существует вывод 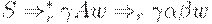, где 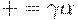и либо a - первый символ w, либо w = e и a = $.

Будем говорить, что ситуация допустима, если она допустима для какого-либо активного префикса.

Пример 4.11. Дана грамматика G = ({S, B}, {a, b}, P, S) с правилами

S -> BB

B -> aB | b

Существует правосторонний вывод 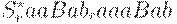. Легко видеть, что ситуация [B -> a.B, a] допустима для активного префикса + = aaa, если в определении выше положить 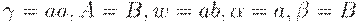. Существует также правосторонний вывод 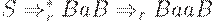. Поэтому для активного префикса Baa допустима ситуация [B -> a.B, $].

Центральная идея метода заключается в том, что по грамматике строится детерминированный конечный автомат, распознающий активные префиксы. Для этого ситуации группируются во множества, которые и образуют состояния автомата. Ситуации можно рассматривать как состояния недетерминированного конечного автомата, распознающего активные префиксы, а их группировка на самом деле есть процесс построения детерминированного конечного автомата из недетерминированного.

Анализатор, работающий слева-направо по типу сдвиг- свертка, должен уметь распознавать основы на верхушке магазина. Состояние автомата после прочтения содержимого магазина и текущий входной символ определяют очередное действие автомата. Функцией переходов этого конечного автомата является функция переходов LR-анализатора.

Чтобы не просматривать магазин на каждом шаге анализа, на верхушке магазина всегда хранится то состояние, в котором должен оказаться этот конечный автомат после того, как он прочитал символы грамматики в магазине от дна к верхушке. Рассмотрим ситуацию вида 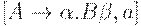из множества ситуаций, допустимых для некоторого активного префикса z. Тогда существует правосторонний вывод 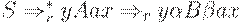, где 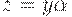. Предположим, что из 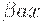выводится терминальная строка bw. Тогда для некоторого правила вывода вида B -> q имеется вывод 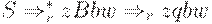. Таким образом [B -> .q, b] также допустима для z и ситуация 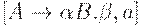допустима для активного префикса zB. Здесь либо b может быть первым терминалом, выводимым из 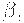либо из 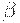выводится e в выводе 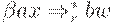и тогда b равно a. То есть b принадлежит 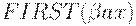. Построение всех таких ситуаций для данного множества ситуаций, то есть его замыкание, делает приведенная ниже функция closure.

Система множеств допустимых LR(1)-ситуаций для всевозможных активных префиксов пополненной грамматики называетсяканонической системой множеств допустимых LR(1)-ситуаций. Алгоритм построения канонической системы множеств приведен ниже.

Алгоритм 4.10. Конструирование канонической системы множеств допустимых LR(1)-ситуаций.

Вход. КС-грамматика G = (N, T, P, S).

Выход. Каноническая система C множеств допустимых LR(1)-ситуаций для грамматики G.

Метод. Выполнить для пополненной грамматики G' процедуру items, которая использует функции closure и goto.

Если I - множество ситуаций, допустимых для некоторого активного префикса +, то goto(I, X) - множество ситуаций, допустимых для активного префикса +X.

Работа алгоритма построения системы C множеств допустимых LR(1)-ситуаций начинается с того, что в C помещается начальное множество ситуаций I₀ = closure({[S' -> .S, $]}). Затем с помощью функции goto вычисляются новые множества ситуаций и включаются в C.

По-существу, goto(I, X) - переход конечного автомата из состояния I по символу X.

Рассмотрим теперь, как по системе множеств LR(1)-ситу- аций строится LR(1)-таблица, то есть функции действий и переходов LR(1)-анализатора.

Алгоритм 4.11. Построение LR(1)-таблицы.

Вход. Каноническая система C = {I₀, I₁, ... , I_n} множеств допустимых LR(1)-ситуаций для грамматики G.

Выход. Функции Action и Goto, составляющие LR(1)- таблицу для грамматики G.

Метод. Для каждого состояния i функции Action[i, a] и Goto[i, X] строятся по множеству ситуаций I_i:

1. Значения функции действия ( Action ) для состояния i определяются следующим образом:

1. если (a - терминал) и goto(I_i, a)= I_j, то полагаем Action[i, a] = shift j;

2. если 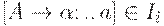, причем 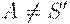, то полагаем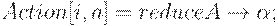

3. если 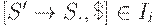, то полагаем Action[i, $] = accept.

2. Значения функции переходов для состояния i определяются следующим образом: если goto(I_i, A) = I_j, то Goto[i, A] = j (здесь A - нетерминал).

3. Все входы в Action и Goto, не определенные шагами 2 и 3, полагаем равными error.

4. Начальное состояние анализатора строится из множества, содержащего ситуацию [S' -> .S, $].

Таблица на основе функций Action и Goto, полученных в результате работы алгоритма 4.11., называется канонической LR(1)-таблицей. Работающий с ней LR(1)-анализатор, называется каноническим LR(1)-анализатором.

Пример 4.12. Рассмотрим следующую грамматику, являющуюся пополненной для грамматики из примера 4.8.:

(0) E' -> E

(1) E -> E + T

(2) E -> T

(3) T -> T * F

(4) T -> F

(5) F -> id.

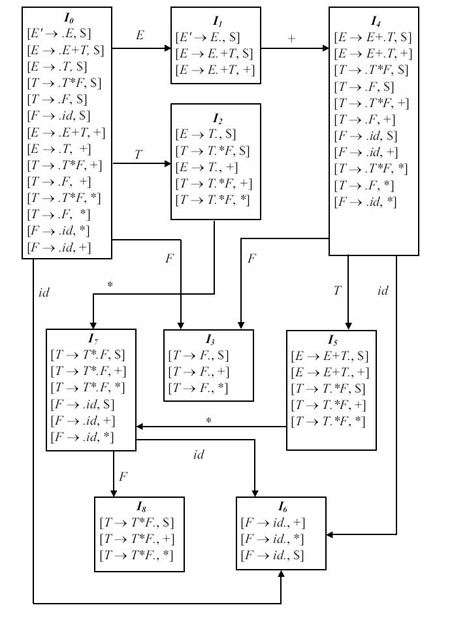
Множества ситуаций и переходы по goto для этой грамматики приведены на рис. 4.9. LR(1)-таблица для этой грамматики приведена на рис. 4.7.

Проследим последовательность создания этих множеств более подробно.

1. Вычисляем I₀ = closure({[E' -> .E, $]}).

1. Ситуация [E' -> .E, $] попадает в него по умолчанию как исходная.

2. Если обратиться к обозначениям функции closure, то для нее

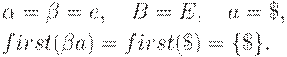
Значит, для терминала $ добавляем ситуации на основе правил со знаком E в левой части правила. Это правила

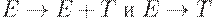
и соответствующие им ситуации

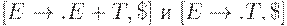
3. Просматриваем получившиеся ситуации. Для ситуации [E ->.E + T, $] , поэтому 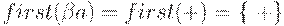. На основе этого добавляем к I₀ [E -> E + .T, +] и [E ->.T, +].

4. Для ситуации . Поэтому добавляем к I₀ [T ->. T * F, $] и [T ->.F, $].

5. Подобно этому для ситуации . Поэтому добавляем к I₀ [T ->.T * F, +] и [T ->.F, +].

6. Из ситуации 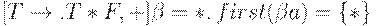: Поэтому добавляем к I₀

увеличить изображение
Рис. 4.9.

[T ->.T * F, *] и [T ->.F, *]

7. Далее из ситуации [T ->.F, *] получаем ситуацию [F ->. id, *]. из ситуации [T ->. F, $] - ситуацию [F ->. id, $], а из ситуации [T ->. F, +] - [F ->. id, +].

Таким образом, все 14 искомых ситуаций I₀ получены.

Возвращаемся в головную функцию items, включаем I₀ в множество C и исследуем непустые итоги применения функцииgoto(I₀; X), где .

Если посмотреть на вид правил в функции goto(I₀; X), то видно, что X должен встретиться в правой части хотя бы одного правила. Для E0 таких правил у нас нет, поэтому значение функции goto(I₀, E') пусто.

Возьмем goto(I0; E). E встречается после точки в правых частях двух ситуаций из I0, значит берем эти два правила и переносим в них точки на один символ вправо (пока есть куда - не уперлись в запятую), получаем:

[E' -> E., $]

и

[E -> E. + T, $|+]

Вычислим от каждой из этих ситуаций функцию closure. Но, поскольку справа от точки здесь либо пустая цепочка, либо терминал, то никаких новых ситуаций не возникает. Дальше отслеживаем, может ли куда-то сдвинуться точка дальше на право и по какому символу. Если может, строим соответствующее множество ( рис. 4.9). И т.д.

LR(1)-грамматики

Если для КС-грамматики G функция Action, полученная в результате работы алгоритма 4.11., не содержит неоднозначно определенных входов, то грамматика называется LR(1)- грамматикой.

Язык L называется LR(1)-языком, если он может быть порожден некоторой LR(1)-грамматикой.

Иногда используется другое определение LR(1)-грамматики. Грамматика называется LR(1), если из условий

1.

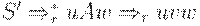
2.

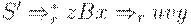
3. FIRST(w)=FIRST(y)

следует, что uAy = zBx (то есть u = z, A = B и x = y).

Согласно этому определению, если uvw и uvy - правовыводимые цепочки пополненной грамматики, у которых FIRST(w) = FIRST(y) и 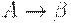- последнее правило, использованное в правом выводе цепочки uvw, то правило 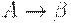должно применяться и в правом разборе при свертке uvy к uAy. Так как A дает 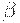независимо от w, то LR(1)-условие означает, что вFIRST(w) содержится информация, достаточная для определения того, что uv за один шаг выводится из uA. Поэтому никогда не может возникнуть сомнений относительно того, как свернуть очередную правовыводимую цепочку пополненной грамматики.

Можно доказать, что эти два определения эквивалентны. Дадим теперь определение LR(k)-грамматики.

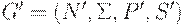Определение. Пусть - КС-грамматика и - полученная из нее пополненная грамматика. Будем называть G LR(k)-грамматикой для k >= 0, если из условий

(1)

(2)

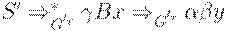
(3) FIRST_k(w) = FIRST_k(y)

следует, что :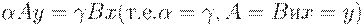

Грамматика G называется LR-грамматикой, если она LR(k)-грамматика для некоторого k >= 0:

Интуитивно это определение говорит о том, что есл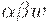и и 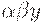- правовыводимые цепочки пополненной грамматики, у которых FIRST_k(w) = FIRST_k(y), и 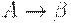- последнее правило, использованное в правом выводе цепочки 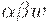, то правило 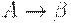должно использоваться также в правом разборе при свертке 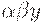к 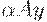. Так как A даeт 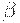независимо от w, то LR(k)-условие говорит о том, что в FIRSTk(w) содержится информация, достаточная для определения того, что 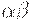за один шаг выводится из 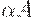. Поэтому никогда не может возникнуть сомнений относительно того, как свернуть очередную правовыводимую цепочку пополненной грамматики. Кроме того, работая с LR(k)-грамматикой, мы всегда знаем, допустить ли данную входную цепочку или продолжать разбор.

Пример 4.13. Рассмотрим грамматику G с правилами

S -> Sa|a

Согласно определению, G не LR(0)-грамматика, так как из трeх условий

(1)

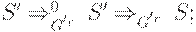
(2)

(3) FIRST₀(e) = FIRST₀(a) = e

не следует, что S'a = S: Применяя определение к этой ситуации, имеем . Проблема здесь заключается в том, что нельзя установить, является ли S основой правовыводимой цепочки Sa, не видя символа, стоящего после S (т.е. наблюдая "нулевое" количество символов). В соответствии с интуицией G не должна быть LR(0)- грамматикой и она не будет ею, если пользоваться первым определением. Это определение мы и будем использовать далее.

Пример 4.14. Пусть G - леволинейная грамматика с правилами

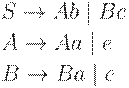
Заметим, что G не является LR(k)-грамматикой ни для какого k.

Допустим, что G - LR(k)-грамматика. Рассмотрим два правых вывода в пополненной грамматике G':

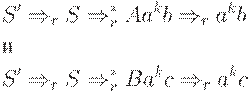
Эти два вывода удовлетворяют условию из определения LR(k)- грамматики при 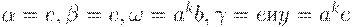: Но так как заключение неверно, т.е. , то G - не LR(k)-грамматика. Более того, так как LR(k)-условие нарушается для всех k, то G - не LR-грамматика.

Если грамматика не является LR(1), то анализатор типа сдвиг-свертка при анализе некоторой цепочки может достигнуть конфигурации, в которой он, зная содержимое магазина и следующий входной символ, не может решить, делать ли сдвиг или свертку (конфликт сдвиг/свертка), или не может решить, какую из нескольких сверток применить (конфликт свертка/свертка).

В частности, неоднозначная грамматика не может быть LR(1). Для доказательства рассмотрим два различных правых вывода

(1)

(2) ,

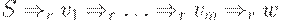Нетрудно заметить, что LR(1) - условие (согласно второму определению LR(1)-грамматики) нарушается для наименьшего из чиселi, для которых .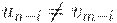

Пример 4.15. Рассмотрим ещe раз грамматику условных операторов:

Если анализатор типа сдвиг-свертка находится в конфигурации, такой, что необработанная часть входной цепочки имеет вид else ... $, а в магазине находится ... if E then S, то нельзя определить, является ли if E then S основой, вне зависимости от того, что лежит в магазине ниже. Это конфликт сдвиг/свертка. В зависимости от того, что следует на входе за else, правильной может быть свертка по S -> if E then S или сдвиг else, а затем разбор другого S и завершение основы if E then S else S. Таким образом нельзя сказать, нужно ли в этом случае делать сдвиг или свертку, так что грамматика не является LR(1).

Эта грамматика может быть преобразована к LR(1)-виду следующим образом:

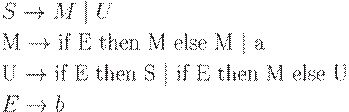
Основная разница между LL(1)- и LR(1)- грамматиками заключается в следующем. Чтобы грамматика была LR(1)- грамматикой, необходимо распознавать вхождение правой части правила вывода, просмотрев все, что выведено из этой правой части и текущий символ входной цепочки. Это требование существенно менее строгое, чем требование для LL(1)-грамматики, когда необходимо определить применимое правило, видя только первый символ, выводимый из его правой части. Таким образом, класс LL(1)-грамматик есть собственный подкласс класса LR(1)-грамматик.

Справедливы также следующие утверждения [2].

Теорема 4.7. Каждый LR(1)-язык является детерминированным КС-языком.

Теорема 4.8. Если L - детерминированный КС-язык, то существует LR(1)-грамматика, порождающая L.

Теорема 4.9. Для любой LR(k)-грамматики для k > 1 существует эквивалентная ей LR(k \Gamma 1)-грамматика.

Доказано, что проблема определения, порождает ли грамматика LR-язык, является алгоритмически неразрешимой.