Конструирование таблицы предсказывающего анализатора

Для конструирования таблицы предсказывающего анализатора по грамматике G может быть использован алгоритм, основанный на следующей идее. Предположим, что 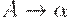- правило вывода грамматики и 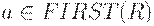. Тогда анализатор делает развертку A по , если входным символом является a. Трудность возникает, когда или 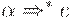. В этом случае нужно развернуть A в 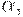если текущий входной символ принадлежит FOLLOW(A) или если достигнут $ и .

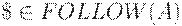Алгоритм 4.7. Построение таблицы предсказывающего анализатора.

Вход. КС-грамматика G = (N, T, P, S).

Выход. Таблица M[A; a] предсказывающего анализатора, .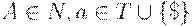

Метод. Для каждого правила вывода 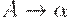грамматики выполнить шаги 1 и 2. После этого выполнить шаг 3.

(1) Для каждого терминала a из FIRST(R) добавить A->R к M[A; a].

(2) Если 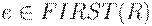, добавить A -> R к M[A; b] для каждого терминала b из FOLLOW(A). Кроме того, есл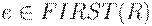и и 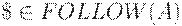, добавить 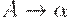к M[A; $].

(3) Положить все неопределенные входы равными "ошибка".

Пример 4.5. Применим алгоритм 4.7 к грамматике из примера 4.3. Поскольку FIRST(TE') = FIRST(T) = {(, id }, в соответствии с правилом вывода E -> TE' входы M[E, ( ] и M[E, id ] становятся равными E -> TE'.

В соответствии с правилом вывода E' -> +TE' значение M[E', +] равно E' -> +TE'. В соответствии с правилом вывода E' -> e значения M[E', )] и M[E', $] равны E' -> e, поскольку FOLLOW(E') = { ), $}.

Таблица анализа, построенная по алгоритму 4.7. для этой грамматики, приведена в таблица 4.3.

LL(1)-грамматики

Алгоритм 4.7 построения таблицы предсказывающего анализатора может быть применен к любой КС-грамматике. Однако для некоторых грамматик построенная таблица может иметь неоднозначно определенные входы. Например, нетрудно доказать, что если грамматика леворекурсивна или неоднозначна, таблица будет иметь по крайней мере один неоднозначно определенный вход.

Грамматики, для которых таблица предсказывающего анализатора не имеет неоднозначно определенных входов, называются LL(1)-грамматиками. Предсказывающий анализатор, построенный для LL(1)-грамматики, называется LL(1)-анализатором. Первая буква L в названии связано с тем, что входная цепочка читается слева направо, вторая L означает, что строится левый вывод входной цепочки, 1 - что на каждом шаге для принятия решения используется один символ непрочитанной части входной цепочки.

Доказано, что алгоритм 4.7 для каждой из LL(1)-грам- матик G строит таблицу предсказывающего анализатора, распознающего все цепочки из L(G) и только эти цепочки. Нетрудно доказать также, что если G - LL(1)-грамматика, то L(G) - детерминированный КС-язык.

Справедлив также следующий критерий LL(1)-граммати- ки. Грамматика G = (N, T, P, S) является LL(1)-грамматикой тогда и только тогда, когда для каждой пары правил 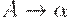, 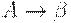из P

(то есть правил с одинаковой левой частью) выполняются следующие 2 условия:

(1)

(2) Если , то .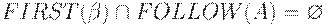

Язык, для которого существует порождающая LL(1)- грамматика, называют LL(1)-языком. Доказано, что проблема определения, порождает ли грамматика LL-язык, является алгоритмически неразрешимой.

Пример 4.6.Неоднозначная грамматика не является LL(1). Примером может служить следующая грамматика

Эта грамматика является неоднозначной, что иллюстрируется на рис. 4.4.

LL(k)-грамматики

Определение. КС-грамматика 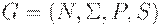называется LL(k)-грамматикой для некоторого фиксированного k, если из

(1)

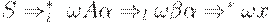
(2) 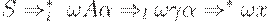для которых

и

FIRST_k(x) = FIRST_k(y), вытекает, что .

Говоря менее формально, G будет LL(k)- грамматикой, если для данной цепочки 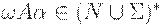и первых k символов (если они есть), выводящихся из 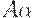, существует не более одного правила, которое можно применить к A, чтобы получитьвывод какой-нибудь терминальной цепочки,

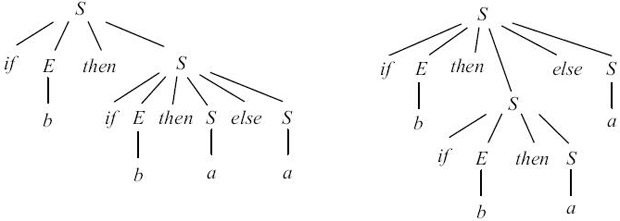
Рис. 4.4.

начинающейся с 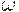и продолжающейся упомянутыми k терминалами.

Грамматика называется LL(k)-грамматикой, если она LL(k)-грамматика для некоторого k.

Пример 4.7. Рассмотрим грамматику G = ({S, A, B}, {0, 1, a, b}, P, S), где P состоит из правил

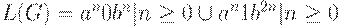Здесь . G не является LL(k)-грамматикой ни для какого k. Интуитивно, если мы начинаем с чтения достаточно длинной цепочки, состоящей из символов a, то не знаем, какое из правил S -> A и S -> B было применено первым, пока не встретим 0 или 1.

Обращаясь к точному определению LL(k)-грамматики, положим 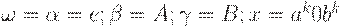и y = a^k1b^2k. Тогда выводы

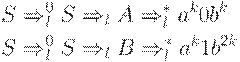
соответствуют выводам (1) и (2) определения. Первые k символов цепочек x и y совпадают. Однако заключение ложно. Так как k здесь выбрано произвольно, то G не является LL-грамматикой.