Следствия определения LL(k)- грамматики

Теорема 4.6. КС-грамматика 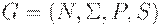является LL(k)-грамматикой тогда и только тогда, когда для двух различных правил 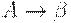и и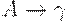з Р пересечение пусто при всех таких , что .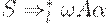

Доказательство. Необходимость. Допустим, что 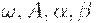и 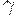удовлетворяют условиям теоремы, а содержит x. Тогда по определению FIRST для некоторых y и z найдутся выводы

(Заметим, что здесь мы использовали тот факт, что N не содержит бесполезных нетерминалов, как это предполагается для всех рассматриваемых грамматик.) Если |x| < k ; то y = z = e. Так как 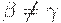, то G не LL(k)-грамматика.

Достаточность. Допустим, что G не LL(k)-грамматика.

Тогда найдутся такие два вывода

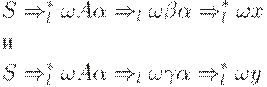
что цепочки x и y совпадают в первых k позициях, но 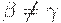. Поэтому 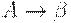и 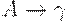- различные правила из Pи каждое из множеств 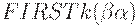и 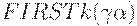содержит цепочку FIRST_k(x), совпадающую с цепочкойFIRST_k(y).

Пример 4.8. Грамматика G, состоящая из двух правил S -> aS | a, не будет LL(1)-грамматикой, так как

FIRST₁(aS) = FIRST₁(a) = a.

Интуитивно это можно объяснить так: видя при разборе цепочки, начинающейся символом a, только этот первый символ, мы не знаем, какое из правил S -> aS или S -> a надо применить к S. С другой стороны, G - это LL(2)-грамматика. В самом деле, в обозначениях только что представленной теоремы, если 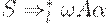, то A = S и . Так как для S даны только два указанных правила, т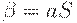о и . Поскольку FIRST2(aS) = aa и FIRST2(a) = a, то по последней теоремеG будет LL(2)-грамматикой.