Удаление левой рекурсии

Основная трудность при использовании предсказывающего анализа - это нахождение такой грамматики для входного языка, по которой можно построить таблицу анализа с однозначно определенными входами. Иногда с помощью некоторых простых преобразований грамматику, не являющуюся LL(1), можно привести к эквивалентной LL(1)-грамматике. Среди этих преобразований наиболее эффективными являются левая факторизация и удаление левой рекурсии. Здесь необходимо сделать два замечания. Во-первых, не всякая грамматика после этих преобразований становится LL(1), и, во-вторых, после таких преобразований получающаяся грамматика может стать менее понимаемой.

Непосредственную левую рекурсию, то есть рекурсию вида 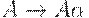, можно удалить следующим способом. Сначала группируем A -правила:

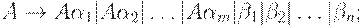
где никакая из строк 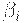не начинается с A. Затем заменяем этот набор правил на

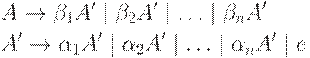
где A' - новый нетерминал. Из нетерминала A можно вывести те же цепочки, что и раньше, но теперь нет левой рекурсии. С помощью этой процедуры удаляются все непосредственные левые рекурсии, но не удаляется левая рекурсия, включающая два или более шага. Приведенный ниже алгоритм 4.8 позволяет удалить все левые рекурсии из грамматики.

Алгоритм 4.8. Удаление левой рекурсии.

Вход. КС-грамматика G без e-правил (вида A -> e ).

Выход. КС-грамматика G' без левой рекурсии, эквивалентная G.

Метод. Выполнить шаги 1 и 2.

(1) Упорядочить нетерминалы грамматики G в произвольном порядке.

(2) Выполнить следующую процедуру:

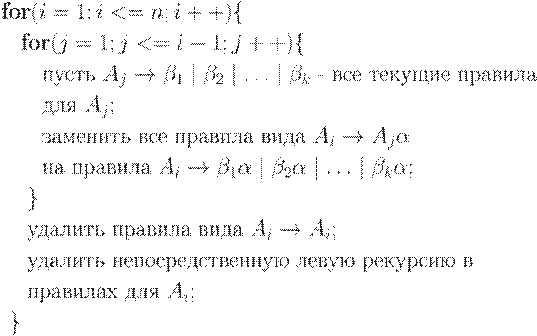
После (i-1) -й итерации внешнего цикла на шаге 2 для любого правила вида 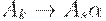, где k < i, выполняется s > k. В результате на следующей итерации (по i ) внутренний цикл (по j ) последовательно увеличивает нижнюю границу по m в любом правиле , пока не будет m >= i. Затем, после удаления непосредственной левой рекурсии для A_i -правил, m становится больше i.

Алгоритм 4.8 применим, если грамматика не имеет e - правил (правил вида A -> e ). Имеющиеся в грамматике e - правила могут быть удалены предварительно. Получающаяся грамматика без левой рекурсии может иметь e -правила.

Левая факторизация

Oсновная идея левой факторизации в том, что в том случае, когда неясно, какую из двух альтернатив надо использовать для развертки нетерминала A, нужно изменить A -правила так, чтобы отложить решение до тех пор, пока не будет достаточно информации для принятия правильного решения.

Если 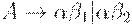- два A -правила и входная цепочка начинается с непустой строки, выводимой из 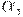мы не знаем, разворачивать ли по первому правилу или по второму. Можно отложить решение, развернув 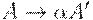. Тогда после анализа того, что выводимо из 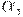можно развернуть по или по 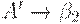. Левофакторизованные правила принимают вид

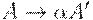
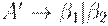
Алгоритм 4.9. Левая факторизация грамматики.

Вход. КС-грамматика G.

Выход. Левофакторизованная КС-грамматика G', эквивалентная G.

Метод. Для каждого нетерминала A найти самый длинный префикс 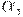общий для двух или более его альтернатив. Если 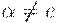, то есть существует нетривиальный общий префикс, заменить все A -правила

,

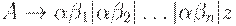где z обозначает все альтернативы, не начинающиеся с 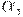на

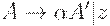
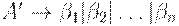
где A' - новый нетерминал. Применять это преобразование, пока никакие две альтернативы не будут иметь общего префикса.

Пример 4.9. Рассмотрим вновь грамматику условных операторов из примера 4.6:

После левой факторизации грамматика принимает вид

К сожалению, грамматика остается неоднозначной, а значит, и не LL(1)-грамматикой.

Рекурсивный спуск

Выше был рассмотрен один из вариантов таблично-управ- ляемого предсказывающего анализа, когда магазин явно использовался в процессе работы анализатора. Возможен иной вариант предсказывающего анализа, в котором каждому нетерминалу сопоставляется процедура (вообще говоря, рекурсивная), и магазин образуется неявно при вызовах таких процедур. Процедуры рекурсивного спуска могут быть записаны, как показано ниже.

В процедуре A для случая, когда имеется правило A -> u_i, такое, что (напомним, что не может быть больше одного правила, из которого выводится e ), приведены два варианта - 1.1 и 1.2. В варианте 1.1 делается проверка, принадлежит ли следующий входной символ FOLLOW(A): Если нет - выдается ошибка. В варианте 1.2 этого не делается, так что анализ ошибки откладывается на процедуру, вызвавшую A.