Уравнения предельного равновесия для сыпучих и связных грунтов
Угол наибольшего отклонения. При действии на поверхность грунта местной нагрузки в любой точке грунта М для любой площадки тп, проведенной через эту точку под углом а (рис. 64, а), возникнут нормальные и касательные напряжения. К нормальным напряжениям при математическом рассмотрении вопроса следует отнести и силы связности, суммарно оцениваемые [см. формулу (11.23')] давлением связности рг. Тогда на площадку тп (рис. 64, а) будут действовать нормальное напряжение оа+ре и касательное Та .
При изменении угла а величина составляющих напряжений также будет меняться и, если касательные (сдвигающие) напряжения достигнут определенной доли от нормальных, то, как показывают опыты на сдвиг, произойдет скольжение одной части грунта по другой.
Таким образом, условием предельного равновесия грунта в данной точке будет
Та < !(Оа + Ре)
или
Оа + рг
Если / — величина постоянная, то, как показано в гл. II, в предельном состоянии она представляет собой тангенс угла наклона прямолинейной огибающей кругов предельных напряжений (рис. 64, б, в).
С другой стороны, согласно рис. 64, а
Та
аа + Р>
= *8в.
Это отношение равно тангенсу угла отклонения 9, т. е. угла, на который отклоняется полное напряжение для площадки о от нормали к этой площадке.
| УУ* \ 4 | \ ___■—7 | ||||
| Втая = Я> / | / / V- | ||||
| \ | |||||
| \ Л \ | |||||
| и / | б | ||||
| А бы | с | ||||
| 6, |
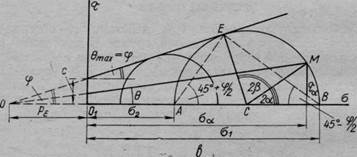
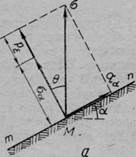
Рис. 64. Круги предельных напряжений:
а — схема напряжений в данной точке; б— диаграмма сдвига для сыпучих грунтов; в — то же, для грунтов связных
Так как через заданную точку можно провести множество площадок, то, очевидно, необходимо отыскать самую невыгодную площадку, для которой будет существовать максимальный угол отклонения бтах- Тогда
1§ бтах ^
Условия предельного равновесия. Для сыпучих грунтов согласно диаграмме сдвига (см. рис. 64, б) максимальное значение угла отклонения бтах будет тогда, когда огибающая ОЕ коснется круга предельных напряжений.
Как было показано ранее (см. гл. II, § 4) и что вытекает из геометрических соотношений, поставленному условию удовлетворяет
120 равенство (11.24):
ОЧ — 02 01 + 02
31П ф,
где 01 и 02 — главные напряжения;
Ф — угол внутреннего трения грунта.
Это и есть условие предельного равновесия для сыпучих грунтов. Ему можно придать несколько другой вид после несложных тригонометрических преобразований, а именно
02 = 01
1 — 51П ф 1 + 51Пф
или
— = 18а(45°=Рф/2)
(11.24")
Последнее выражение весьма широко используется в теории давления грунтов на ограждения, причем знак «минус» (в скобках) соответствует так называемому активному давлению, а знак «плюс» — пассивному сопротивлению сыпучих грунтов.
Условию предельного равновесия для сыпучих грунтов иногда придают иной вид, выразив главные напряжения 01 и 02 через составляющие напряжения о2, ау и хуг (для плоской задачи). Тогда будем иметь следующее выражение, тождественное зависимости (11.24):
(02 — 0^)2 +4т
(0у + ог)<
5Ш2ф.
(11.24'")
Для связных грунтов, подобно предыдущему, пользуясь диаграммой предельных напряжений (рис. 64, в), получим условие предельного равновесия в виде
01 — 02
01 + 02 + 2/?е
= 51П ф,
(11.25')
откуда
01 — 02 :
2 5 ИТ
+ 0"2
(11.25")
а так как согласно формуле (11.23')
ссгдф,
где с — сцепление грунта, определяемое как начальный параметр огибающей кругов предельных напряжений, то уравнение (11.25") может быть представлено в виде 1
01 — о%
С05 ф
С1 + 02 *ёф-о- = С.
(11.25'")
Последняя формула широко используется в задачах теории предельного равновесия.
Условие предельного равновесия в составляющих напряжениях сг, оу, х для связных грунтов имеет следующий вид:
(Ох — Оу) 2 + 4туг (аг + ау-г-2сс1§ф)
- = 5Ш2ф.
(11.25^)
Отметим, что круг предельных напряжений дает возможность определить направления площадок скольжения для любой заданной точки.
Если соединить точку касания предельной прямой ОЕ (рис. 64, в) с концом отрезка, изображающего в масштабе о2 (точка А), то направление ЕА определит направление площадки скольжения. По рис. 64, 8
/_ВСЕ = 2|3 = 90° + ф,
откуда
= 45° + ф/2.
Таким образом, в условиях предельного равновесия площадки скольжения будут наклонены под углом ±(45° + ф/2) к направлению площадки наибольшего главного напряжения, или, что то же самое, под углом ± (45°—ф/2) к направлению главного напряжения 0\.
Дифференциальные уравнения равновесия грунтов в предельно-напряженном состоянии. Плоская задача. В общем случае напряженного состояния для условий плоской задачи дифференциальные уравнения равновесия для любых линейно деформируемых тел при горизонтальной ограничивающей полупространство плоскости (направление оси У,— горизонтально, оси 2 — вертикально), как известно из теории упругости, записываются в следующем виде:
| доу | дхУх |
| ду | дг |
| дох | дхух |
| дг | ду |
0;
(а!)
(ая)
где ог>У> 1уг составляющие напряжении;
у — объемный вес грунта.
В этих двух дифференциальных уравнениях три неизвестных (ог, оу и хуг); таким образом, задача является (без добавочных условий) статически неопределимой. Если же добавить к этим двум уравнениям третье, например, (П.251У), то получим замкнутую систему трех уравнений с тремя неизвестными, но для предельного напряженного состояния, так как уравнение (П.251У) является условием предельного равновесия:
(Ог — ау)2 + 4т.
1/2
(ог + Оу + 2сС1§ф)2
= 51П2 ф.
(аз)
Таким образом, задача в общей постановке статически определима.
Решение дифференциальных уравнений равновесия (а1) и (аг) совместно с условием предельного равновесия (аз) в дальнейшем получено (проф. В. В. Соколовским, 1942 г.) как системы уравнений гиперболического типа.
Пространственная задача имеет замкнутую систему уравнений (статически определимую) только для случая осевой симметрии.
Для осесимметричной задачи, воспользовавшись цилиндрической системой координат (г, т>) и приняв обозначения составляющих напряжений по рис. 65, имеем следующую систему уравнений равновесия:
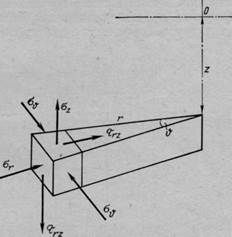
Рис. 65. Схема пространственной
напряжении в случае осесимметричной задачи
дог
1/7 +
дог
дг
~дг'
дхг
От — 0>
= 0;
Хгг
дг
(61)
(62)
Условие предельного равновесия в цилиндрической системе координат запишется так:
(Ог— Сг)2"}- 4тгг
{ог + о2 + 2с с1§уУ
= ЗШ^ф.
(бз)
Кроме того, вследствие симметрии касательные напряжения по меридиональным плоскостям равны нулю, поэтому напряжение является главным и, кроме того, для осесимметричной задачи
00 = 02 == 03- (64)
Уравнение (б4) и является добавочным к системе уравнений (61) — (б3) и делает ее статически определимой. Приведенная система уравнений предельного равновесия (61) — (б4) для осесимметричной задачи (сформулированная проф. В. Г. Березанцевым, 1952 г.) соответствует случаю деформаций грунта от оси симметрии 02. Некоторые важные случаи решения этой задачи приведены ниже.
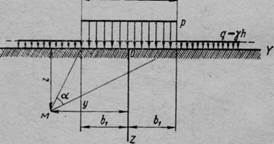
Рис. 66. Схема действия полосообразной нг грузки
Дата добавления: 2016-06-02; просмотров: 3157;
