Распределение напряжений в случае плоской задачи
Условия плоской задачи будут иметь место тогда, когда напряжения распределяются в одной плоскости, в направлении же перпендикулярном они или будут равны нулю, или постоянны. Это условие имеет место для очень вытянутых в плане сооружений, например ленточных и стеновых фундаментов, оснований подпорных стенок, насыпей, дамб и подобных сооружений. Для этих сооружений в любом месте, за исключением лишь краевых участков от края по длине (примерно 2—3 ширины сооружения), распределение напряжений в любом проведенном сечении будет таким же, как и в других соседних, при условии, что в направлении, перпендикулярном рассматриваемой плоскости, нагрузка не меняется.
Определение напряжений в условиях плоской задачи значительно упрощается и во многих случаях может быть представлено в удобной форме.
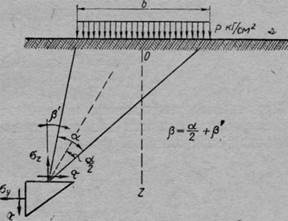
Рис. 47. Схема действия равномерно распределенной нагрузки
в условиях плоской задачи
Следует также отметить весьма важное свойство плоской задачи, заключающейся в том, что все составляющие напряжений ог, оу и % в рассматриваемой плоскости 20 У не зависят от деформационных характеристик линейно деформируемого полупространства (модуля общей деформации и коэффициента поперечной деформации), т. е. будут справедливы для всех тел (сплошных, сыпучих и т. п.), для которых зависимость между напряжениями и деформациями может быть принята линейной.
Плоская задача определения напряжений для линейно деформируемых тел в настоящее время детально разработана в трудах Прандтля, Митчела, Г. В. Колосова, Н. П. Пузыревского, Н. М. Гер-севанова и др. Мы здесь ограничимся приведением только наиболее часто применяемых на практике решений. Эти решения получены следующим методом.
Используя формулы для напряжений в линейно деформируемом массиве от погонной нагрузки (Фламана) в условиях плоской задачи путем интегрирования напряжений от действия элементарных сил (рйу-\), получают выражения для составляющих напряжений а2, оу, х для различных видов распределенных нагрузок: равномерной, возрастающей по закону прямой и др.
Действие равномерно распределенной нагрузки. Схема действия равномерно распределенной нагрузки в условиях плоской задачи показана на рис. 47. Если обозначить буквой а угол видимости, ос
р = — + р' (где р" — угол, составляемый крайним лучом с вертикалью), то для составляющих напряжений будут справедливы следующие выражения:
Ох
Л
р
(а + 51П асоз 2р);
оу — —(а — 51П а сое 26);
т = —(зта51п2р).
(111.11)
Приведенные выражения позволяют легко составить таблицу коэффициентов влияния для вычисления составляющих напряжений, введя следующие обозначения:
Ох --- КтР;
Т = КухР.
(111.11')
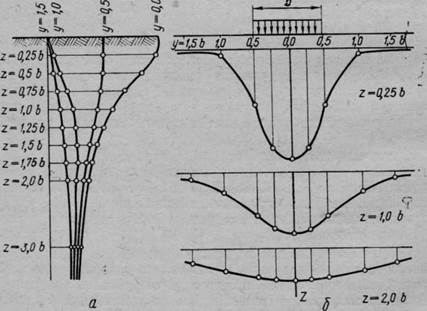
Рис. 48. Эпюры распределения сжимающих напряжений <тг по
вертикальным (а) и горизонтальным (б) сечениям массива грунта
Величины коэффициентов влияния Кг, Ку, Ку? приведены в табл. 12 в зависимости от величины относительных координат г/Ь и у/Ь.
Пользуясь данными табл. 12, легко построить эпюры распределения напряжений по горизонтальным и вертикальным сечениям массива грунта в случае плоской задачи (при полосообразной равномерно распределенной нагрузке).
Как пример на рис. 48 показаны эпюры сжимающих напряжений аг для вертикальных и горизонтальных сечений массива грунта.
Пользуясь полученными эпюрами напряжений, легко построить и кривые равных напряжений. Так, на рис. 49, а приведены линии одинаковых вертикальных сжимающих напряжений или давлений {изобары), на рис. 49, б — линии одинаковых горизонтальных напряжений (распоры) и на рис. 49, в — линии одинаковых касательных напряжений (сдвиги), наглядно характеризующие вею напряженную область грунта под полосообразной нагрузкой.
Интересно отметить, что если ограничиться рассмотрением давлений, больших 0,1 р, то влияние сжимающих напряжений сказывается в случае плоской задачи на большую глубину (примерно до 6Ь), чем в случае пространственной задачи (например, для квадратной площади загрузки — до 4 Ь).
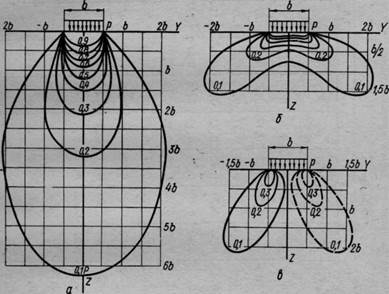
Рис. 49. Линии равных напряжений в линейно деформируемом массиве в случае плоской задачи:
а — изобары ог; б — распоры Оу; в — сдвиги X гх
Область распределения распоров выдвигается в стороны более чем на ширину площади подошвы ленточного фундамента, а макси мальные сдвигающие напряжения (до 0,32 р) имеют место под краями подошвы полосообразной нагрузки; по оси же нагрузки сдвигающие напряжения равны нулю. Для главных напряжений 01 и 02 и для максимальных сдвигающих тШах=(01—0г)/2 линии одинаковых напряжений представляют окружности, проходящие через краевые точки подошвы полосообразной нагрузки.
Главные напряжения, т. е. наибольшие и наименьшие нормальные напряжения, будут для площадок, расположенных по вертикальной оси симметрии нагрузки-. Действительно, для таких площадок угол р'=—а/2 и, следовательно, угол р = а/2 — а/2 = 0.
Таблица 12
Значения коэффициентов влияния /\,, Л'„ и А"у.. для определения составляющих напряжений в случае действия равномерно
распределенной нагрузки в условиях плоской задачи
| Значения у1Ь | ||||||||||||||||||
| 0,25 | 0,5 | 1,5 | ||||||||||||||||
| Кг | «У | КУг | Кг | *ш | КУИ | Кг | «У | КУг | «г | «У | КУг | *2 | КУ | куг | Кг | «в | кУг | |
| 0,00 | 1,00 | 1,00 | 1,00 | 1,00 | 0,50 | 0,50 | 0,32 | |||||||||||
| 0,25 | 0,96 | 0,45 | 0,90 | 0,39 | 0,13 | 0,50 | 0,35 | 0,30 | 0,02 | 0,17 | 0,05 | 0,00 | 0,07 | 0,01 | 0,00 | 0,04 | 0,00 | |
| 0,50 | 0,82 | 0,18 | 0,74 | 0,19 | 0,16 | 0,48 | 0,23 | 0,26 | 0,08 | 0,21 | 0,13 | 0,02 | 0,12 | 0,04 | 0,00 | 0,07 | 0,02 | |
| 0,75 | 0,67 | 0,08 | 0,61 | 0,10 | 0,13 | 0,45 | 0,14 | 0,20 | 0,15 | 0,22 | 0,16 | 0,04 | 0,14 | 0,07 | 0,02 | 0,10 | 0,04 | |
| 1,00 | 0,55 | 0,04 | 0,51 | 0,05 | 0,10 | 0,41 | 0,09 | 0,16 | 0,19 | 0,15 | 0,16 | 0,07 | 0,14 | 0,10 | 0,03 | 0,13 | 0,05 | |
| 1,25 | 0,46 | 0,02 | 0,44 | 0,03 | 0,07 | 0,37 | 0,06 | 0,12 | 0,20 | 0,11 | 0,14 | 0,10 | 0,12 | 0,10 | 0,04 | 0,11 | 0,07 | |
| 1,50 | 0,40 | 0,01 | 0,38 | 0,02 | 0,06 | 0,33 | 0,04 | 0,10 | 0,21 | 0,06 | 0,11 | 0,13 | 0,09 | 0,10 | 0,07 | 0,09 | 0,08 | |
| 1,75 | 0,35 | — | 0,34 | 0,01 | 0,04 | 0,30 | 0,03 | 0,08 | 0,20 | 0,05 | 0,10 | 0,14 | 0,07 | 0,10 | 0,08 | 0,08 | 0,08 | |
| 2,00 | 0,31 | — | 0,31 | — | 0,03 | 0,28 | 0,02 | 0,06 | 0,17 | 0,02 | 0,06 | 0,13 | 0,03 | 0,07 | 0,10 | 0,04 | 0,07 | |
| 3,00 | 0,21 | — | в,21 | — | 9,82 | 0,20 | 0,01 | 0,03 | 9,14 | 0,01 | 0,03 | 0,12 | 0,02 | 0,05 | 0,10 | 0,03 | 0,05 | |
| 4,00 | 0,16 | — | 0,16 | — | в,01 | 8,15 | — | 0,82 | 0,12 | — | — ' | 0,11 | — | — | 0,09 | — | — | |
| 5,00 | 0,13 | — | 0,13 | — | — | 8,12 | — | — | 0,10 | — | — | 0,10 | — | — | — | — | — | |
| 6,00 | 0,11 | — | 0,10 |
Примечание. Величина коэффициентов К, — Кп для относительных глубин (2г/Ь) приведена также в табл. 9 (при а&10).
Тогда согласно третьей строке формулы (111.11) сдвигающее напряжение будет равно т = 0, т. е. площадки будут главными.
Можно показать, что главными площадками будут также площадки, расположенные по биссектрисам углов видимости и площадкам, им перпендикулярным.
Величину главных напряжений получим из выражений (111.11), полагая в них р = 0:
01 = — (а + 51П а);
р
02 = —(а — 81П а). я
(111.12)
Формулы (111.12) весьма часто применяются при оценке напряженного состояния в основаниях сооружений, особенно предельного.
Они дают также возможность построить эллипсы напряжений для различных точек напряженного линейно деформируемого полупространства (рис. 50), наглядно иллюстрирующих изменение напряжений в грунте под полосообразной нагрузкой.
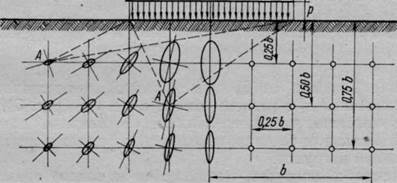
Рис. 50. Эллипсы напряжений при действии равномерно
распределенной нагрузки в условиях плоской задачи
Треугольная нагрузка. При определении напряжений в грунтах от действия неравномерной нагрузки важным составным элементом является треугольная нагрузка, т. е. нагрузка, интенсивность которой меняется по закону треугольника.
Приведем здесь только формулу (ее наиболее простой вид) для величины сжимающих вертикальных напряжений ог, действующих на горизонтальные площадки, параллельные ограничивающей плоскости:
*==0^а-зш2г]: (111.13)
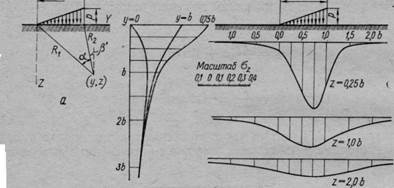
где а и — углы, показанные на рис. 51, а, рад.
На рис. 51, б, в для иллюстрации приведены зпюры распределения сжимающих напряжений ог по горизонтальным и вертикальным сечениям линейно деформируемого массива от действия треугольной нагрузки в долях от ее максимальной интенсивности, а в табл. 13 — значения а2 в зависимости от г/Ь и у/Ь (рис. 51, а).
5 6 о
Рис. 51. Эпюры распределения сжимающих напряжений по вертикальным и горизонтальным сечениям массива грунта при действии треугольной нагрузки
Следует отметить, что максимальные сжимающие напряжения будут в вертикальном сечении, проходящем близко к центру тяжести треугольной нагрузки.
Действие любой нагрузки, меняющейся по закону прямой. Важными случаями действия полосообразной нагрузки будут также нагрузка, меняющаяся по прямоугольному и равностороннему треугольникам, трапецеидальная и т. п., т. е. изменяющиеся по закону-прямой. Формулы для вычисления напряжений для этих случаев нагрузки приведены в ряде руководств и справочников по механике грунтов*. Здесь мы остановимся лишь на применении универсального для рассматриваемого вида нагрузок графика Остерберга, опубликованного в трудах IV Международного конгресса по механике грунтов.
Величина сжимающих напряжений при треугольной нагрузке в долях от р
| 2 * | Значения у | * | |||||||||
| — 1,5 | —1 | —0,5 | 0,25 | 0,5 | 0,75 | 1,5 | 2,5 | ||||
| 0,00" | 0,000 | 0,000 | 0,000 | 0,000 | 0,250 | 0,500 | 0,750 | 0,500 | 0,000 | 0,000 | 0,000 |
| 0,25 | — | — | 0,001 | 0,075 | 0,256 | 0,480 | 0,643 | 0,424 | 0,015 | 0,003 | 0,000 |
| 0,50 | 0,002 | 0,003 | 0,023 | 0,127 | 0,263 | 0,410 | 0,477 | 0,353 | 0,056 | 0,017 | 0,003 |
| 0,75 | 0,006 | 0,016 | 0,042 | 0,153 | 0,248 | 0,335 | 0,361 | 0,293 | 0,108 | 0,024 | 0,009 |
| 1,00 | 0,014 | 0,025 | 0,061 | 0,159 | 0,223 | 0,275 | 0,279 | 0,241 | 0,129 | 0,045 | 0,013 |
| 1,50 | 0,020 | 0,048 | 0,096 | 0,145 | 0,178 | 0,200 | 0,202 | 0,185 | 0,124 | 0,062 | 0,041 |
| 2,00 | 0,033 | 0,061 | 0,092 | 0,127 | 0,146 | 0,155 | 0,163 | 0,153 | 0,108 | 0,069 | 0,050 |
| 3,00 | 0,050 | 0,064 | 0,080 | 0,096 | 0,103 | 0,104 | 0,108 | 0,104 | 0,090 | 0,071 | 0,050 |
| 4,00 | 0,051 | 0,060 | 0,067 | 0,075 | 0,078 | 0,085 | 0,082 | 0,075 | 0,073 | 0,060 | 0,049 |
| 5,00 | 0,047 | 0,052 | 0,057 | 0,059 | 0,062 | 0,063 | 0,063 | 0,065 | 0,061 | 0,051 | 0,047 |
| 6,00 | 0,041 | 0,041 | 0,050 | 0,051 | 0,052 | 0,053 | 0,053 | 0,053 | 0,050 | 0,050 | 0,045 |
Сжимающие напряжения в массиве грунта при нагрузке, меняющейся по закону прямой, вычисляются по формуле
Ох = 1р,
где 1 = 1(а/г, Ь/г)—функция относительных величин (а/г и Ь/г), определяемая по графику (рис. 52) (а и Ь — длина соответственно треугольной и прямоугольной эпюр нагрузки; г-—глубина рассматриваемой точки).
Величина / определяется как алгебраическая сумма коэффициентов, соответствующих нагрузке слева и справа от вертикали, проходящей через рассматриваемую точку.
Поясним сказанное примерами.
Пример 4. Определим напряжение для точки М] (рис. 53, а). При нагрузке, действующей слева,
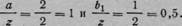
По графику (см. рис. 52) /л =0,397. При нагрузке, действующей справа,
а 2 Ь2 3
— = — = 1 и -Н.-—= 1,5; /п = 0,478. г 2 г 2
Таким образом,
"2, = (/* + 7н) Р
или, подставляя численные значения, получим
ог1 = (0,397 + 0,478) р = 0,875/7.
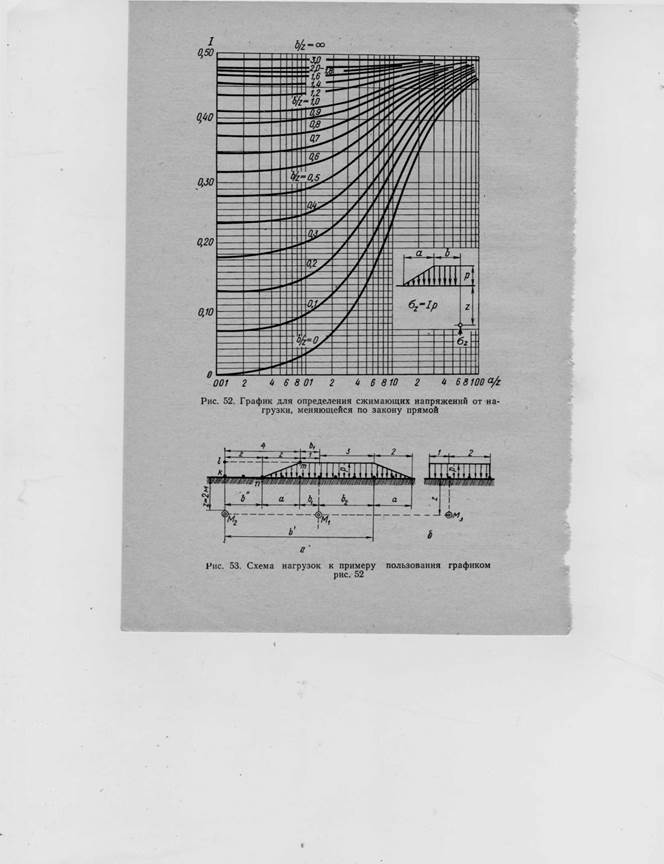
Для определения сжимающего напряжения ог2 в точке Мг (см. рис. 53, а) прикладываем фиктивную нагрузку к1тп. При полной нагрузке (включая фиктивную)
а Ь' 8
— = 1 „ — = — = 4; /„ = 0,499. г г 2
При фиктивной нагрузке
а Ь"
— = 1 и — = 1; /п = 0,455. г г
Подставляя численные значения и учитывая фиктивность нагрузки к1тп, получим
агг (/„ — /„) Р~ (0,499 — 0,455) /7 = 0,044/?, Для случая прямоугольной нагрузки (рис. 53, б)
ст23 = (/л + /п)/>-
Определив /л при а/г = 0 и Ь/г =0,5 и /п при а/г = 0 и Ь/г — 1, получим
агз = (0,278 + 0,410) /7 = 0,688р.
Произвольный вид нагрузки. При произвольном виде сплошной полосообразной нагрузки эпюру внешних давлений разбивают на прямоугольные и треугольные элементы, например, как показано на рис. 54, а, и путем суммирования напряжений от прямоугольных и треугольных элементов эпюры давлений определяют величину сжимающего напряжения в заданной точке грунтового массива.
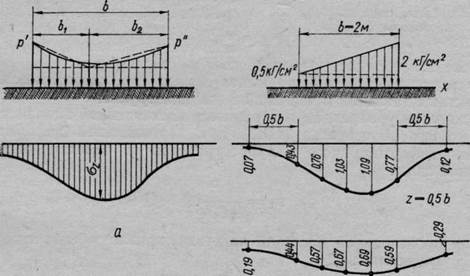
Рис. 54. Схема действия неравномерной нагрузки в случае плоской
задачи:
а разбивка криволинейной эпюры давлений на элементы; б — распределение сжимающих напряжений при действии внешней нагрузки по трапецеидальной
эпюре
Как пример на рис. 54, б приведены эпюры распределения сжимающих напряжений сг2 в грунте на глубине 2=0,5 6 и г=1,0Ь, вычисленные по изложенному способу для случая действия на поверхность грунта давлений, распределенных по трапецеидальной эпюре.
Изложенный способ применим при любом виде эпюры внешних давлений.
§ 3. распределение давлений по подошве сооружений, опирающихся на грунт (контактная задача)
Вопрос о распределении давлений по подошве сооружений имеет большое практическое значение, особенно для гибких фундаментов, рассчитываемых на изгиб.
Если известно реактивное давление по подошве фундамента, которое обычно называют контактным, то, приложив к подошве
фундаментной балки его обратную величину, без особого труда находят величину расчетных изгибающих моментов и перерезывающих сил, применяя обычные уравнения статики.
В предыдущем разделе рассматривалось действие на грунт распределенной нагрузки, которая следовала деформациям поверхности грунта, т. е. нагрузки, передающейся на грунт при посредстве нежесткого тела, например грунтовой насыпи и т. п. Однако большинство фундаментов сооружений обладает определенной жесткостью. Поэтому важно оценить, как жесткость фундамента сказывается на распределении контактных давлений и давлений в массиве грунта.
Исходным уравнением для решения поставленной задачи является формула Буссинеска (Ш.З) для вертикальной деформации линейно деформируемого полупространства от действия сосредоточенной силы:
Р пСаР
Для произвольной площади нагрузки, приняв обозначения по рис. 55, будем иметь
1 Г" г* р{1,тС)й1йг\
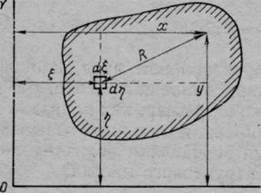
Рис. 55. Схема площади загрузки произвольного вида
где Р — площадь загрузки, по которой должно быть произведено интегрирование.
Если фундамент абсолютно жесткий, то все точки его площади подошвы будут иметь при центральной нагрузке лишь одну и ту же вертикальную деформацию.
Таким образом, условие абсолютной жесткости фундамента дает в этом случае
фг = СОП51
ИЛИ
щ = -1- С Г_Р<ШВ*>-= СОП51. (Ш.15)
яСо 7 1/(х-Е)2 + (г/-л)2
Решение этого интегрального уравнения для круглой площади подошвы при центральной нагрузке абсолютно жесткого фундамента имеет следующий вид:
рху =--, (Ш.16)
где г — радиус подошвы фундамента;
р — расстояние от центра подошвы до любой ее точки (р^О;
рт — среднее давление на единицу площади подошвы.
Для случая плоской задачи
^Рт /тп 1 с/\
рхУ =- —, (Ш.16')
где у— расстояние по горизонтали от середины фундамента до - рассматриваемой точки;
Ь\ — полуширина фундамента. При внецентренной нагрузке Р в случае плоской задачи (по В. А. Гастеву)
Р ^ 2ей 2цЬ, \
рху =--У1 + —+4, (Ш.16")
яУ62-г/2 Ь\ Р
где е — эксцентриситет сосредоточенной (погонной) силы Р;
ц — интенсивность боковой пригрузки.
Если начертить эпюру распределения контактных давлений (рис. 56, а), то для абсолютно жесткого фундамента на линейно деформируемом полупространстве будем иметь седлообразную эпюру с бесконечно большими давлениями по краям.
Действительно, при р = г и при у = Ъ\ рху = <х>. По центральной же оси симметрии фундамента при круглой площади подошвы
Рт „ 9
ро = —— и при ленточной р0 — —рт.
2 я
Однако, как показывают решения, выполненные с учетом ползучести скелета грунта (Н. X. Арутюняном) и одновременно с возрастанием по глубине модуля общей деформации |(Ю. К. Зарецким), контактные давления по подошве жесткого фундамента будут распределяться по значительно более пологой кривой и, кроме того, у края фундамента они не могут быть больше предела несущей способности грунта, что также обусловливает перераспределение давлений по подошве (рис. 56, а, пунктирная линия).

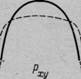
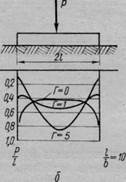
Рис. 56. Эпюры контактных давлений:
а — под абсолютно жестким фундаментом; б — под фундаментами различной гибкости
Концентрация давлений у края жестких фундаментов сказывается на распределении напряжений в массиве грунта лишь на небольшую глубину от подошвы, и общая луковица напряжений мало изменяется, вследствие чего общая осадка фундаментов мало зависит от их жесткости, хотя осадка абсолютно жестких фундаментов, как то вытекает из соответствующих решений (см. гл. V), несколько меньше, чем гибких.
Так, на рис. 57 по вычислениям Института оснований построены изобары для абсолютно жесткого фундамента и для абсолютно гибкого, которые подтверждают высказанное выше положение.
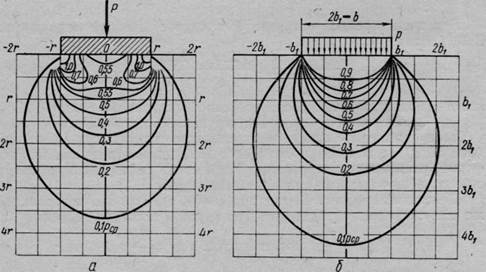
Рис. 57. Изобары в грунте под фундаментами: а — абсолютно жестким; б — гибким
Для подошвы фундаментов эпюра контактных давлений по решениям, излагаемым в курсе сопротивления материалов, будет прямолинейной — равномерной или трапецеидальной, тогда как по строгому решению теории упругости для абсолютно жестких фундаментов она всегда будет седлообразной; для фундаментов же конечной жесткости — может принимать очертание от седлообразного до параболического (см. рис. 56, б).
Для определения контактных давлений в последнем случае интегральное уравнение (111.14) решают совместно с дифференциальным уравнением изгиба балок. В результате оказывается, что распределение контактных давлений в высокой степени зависит от гибкости фундамента Г, которая (по М. И. Горбунову-Посадову) определяется выражением
4(1-р0)2^1/1 * Е,к\ '
где Е0, р0 — модули деформируемости грунта основания;
Е^1 —- жесткость фундаментной балки; / — полудлина балки;
Н\ — высота прямоугольной фундаментной балки.
На рис. 56, б приведено три кривых распределения контактных давлений в зависимости от гибкости фундаментной балки: при Г = 0 (абсолютно жесткой), при Г= 1 и Г = 5.
Следует отметить, что распределение контактных давлений по подошве фундаментов зависит не только от гибкости фундаментов, но и от глубины их заложения, величины внешней нагрузки, обусловливающей развитие пластических деформаций в грунте, а следовательно, и от прочностных свойств грунта.
В заключение укажем, что материалы, изложенные в настоящем разделе, могут служить основой при разработке методов проектирования и расчета фундаментных балок и плит, лежащих на сжимаемом линейно деформируемом полупространстве.
Влияние неоднородности и анизотропии на распределение напряжений в грунтах. Существенное влияние на напряженное состояние грунтов основания имеет не только жесткость фундаментов, но и неоднородность и анизотропность грунтов под фундаментом, резкое изменение модуля деформируемости отдельных слоев грунта и особенно близкое залегание несжимаемых скальных пород. Для сооружений, занимающих большую площадь в плане, когда мощность сжимаемой толщи (до скальной породы) будет порядка ширины загруженной площади или меньше ее, влияние несжимаемой породы существенно сказывается как на распределении напряжений по глубине, так и на величине и распределении контактных давлений.
Распределение сжимающих напряжений в слое грунта ограниченной толщины на несжимаемом основании в случае гибкой полосообразной равномерно распределенной нагрузки было получено (на основе задачи Маргера и Шехтер) в Институте оснований (К. Е. Егоров, 1939 г.); результаты вычислений сведены в табл. 14.
Таблица 14
Дата добавления: 2016-06-02; просмотров: 10641;
