Об устойчивости массивов грунта при оползнях
Причины нарушения устойчивости. Анализ устойчивости массивов грунта имеет очень большое практическое значение при проектировании земляных сооружений: насыпей, выемок, дамб, земляных плотин, современных больших вскрышных котлованов, имеющих иногда глубину 100 м и более, и других подобных сооружений.
Задача устойчивости массивов грунта является частной задачей общей теории предельного напряженного состояния грунтов, но имеет весьма существенные особенности, обусловленные спецификой движения масс при нарушении их устойчивости.
Расчеты устойчивости массивов грунта являются специальным разделом статики, и мы излагаем здесь лишь некоторые основные положения, позволяющие оттенить сущность рассматриваемых задач, и даем наиболее важные приемы их решения, применяемые в проектной практике.
Главнейшими причинами нарушения устойчивости земляных масс будут: 1—эрозионные процессы и 2— нарушение равновесия.
Эрозионные процессы протекают, как правило, весьма медленно, незаметно; зависят они от внешних метеорологических и физико-геологических условий, а также от свойств поверхности массива грунта и обычно не рассматриваются в механике грунтов.
Изучение же условий устойчивости массивов грунта и их нарушений является прямой задачей механики грунтов.
Нарушение равновесия массивов грунта может происходить внезапно со сползанием значительных масс грунта — такие нарушения равновесия называют оползнями. Этот вид нарушений равновесия является наиболее частым и происходит в различного рода откосах и природных склонах как при увеличении действующих на массив нагрузок, так и при уменьшении внутренних сопротивлений.
Увеличение нагрузок может иметь место при возведении сооружений на откосах и склонах при давлении от них, превосходящем некоторый предел, и при изменении веса слоев грунта (его возрастании) при насыщении их водой в условиях продолжительных дождей и паводков, а также вследствие подвешивания капиллярной влаги при понижении уровня грунтовых вод. Уменьшение сопротивлений происходит как при всяком разрушении естественных упоров
139 массивов грунта, так и при уменьшении эффективного трения (при наличии порового давления) и сил сцепления (при увлажнении и набухании грунтов).
Можно различать следующие основные виды оползней: 1 — оползни вращения (с возникающими криволинейными поверхностями обрушения); 2 — оползни скольжения (по зафиксированным поверхностям) и 3 — оползни разжижения (грязевые потоки перенасыщенных водой грунтов по выработанным руслам и тальвегам).
Рассмотрим условия равновесия отдельных видов оползней.
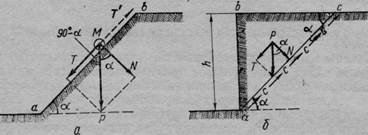
Рис. 75. Схема сил, действующих на частицу откоса идеально сыпучего грунта (а) и на вертикальный массив связного грунта (6)
Устойчивость свободных откосов и склонов. Элементарные задачи. Для установления некоторых понятий рассмотрим две элементарные задачи: 1) устойчивость откоса идеально сыпучего грунта и 2) устойчивость идеально связного массива грунта.
1. Пусть для первого случая имеем откос сыпучего грунта, на котором свободно лежит твердая частица М (рис. 75, а).
Разложим вес частицы Р на две составляющие: нормальную N к линии откоса аЪ и касательную Т. Сила Т стремится сдвинуть частицу к подножию откоса, но ей будет противодействовать сила трения Т', пропорциональная нормальному давлению, т. е. Т'—Щ (где / — коэффициент трения).
Проектируя все силы на наклонную грань откоса, имеем
Р 81П а — /Р соз а = О,
откуда т°;а = /, а так как коэффициент трения ^ = 1§ф, то окончательно получим .
<х = <р. (1У.11)
Таким образом, предельный угол откоса сыпучих грунтов равен углу внутреннего трения грунта. Этот угол носит название угла естественного откоса.
Понятие об угле естественного откоса относится только к сухим сыпучим грунтам, а для грунтов связных глинистых оно теряет всякий смысл, так как у последних в зависимости от их увлажненности угол откоса может меняться от 0 до 90° и зависит также от высоты откоса.
2. Рассмотрим условия равновесия идеально связного грунта (Ф = 0;с^0).
Примем приближенно, что нарушение равновесия при некоторой предельной высоте к произойдет по плоской поверхности скольжения ас, наклоненной под углом а к горизонту (рис. 75, б).
Составим уравнение равновесия всех сил, действующих на оползающую призму аЬс. Действующей силой здесь будет вес Р призмы аЬс.
Принимая во внимание, что согласно рис. 75, б стороны призмы Ьс = к сгр; а, получим
у/г2
— а.
Силу Р разложим на нормальную и касательную к поверхности скольжения ас. Силами, сопротивляющимися скольжению, будут лишь силы сцепления с, распределенные по плоскости скольжения ас = к/ёт а.
Так как в верхней точке с призмы аЬс давление будет равно нулю, а в нижней а — максимальным, то в среднем следует учитывать лишь половину сил сцепления, что элементарным путем позволяет прийти к решению, совпадающему для рассматриваемого случая со строгим решением теории предельного равновесия.
Составим уравнение равновесия, взяв сумму проекций всех сил на направление ас и приравняв ее нулю:
у/г
к
откуда
2 6 2 вша
у/г
с = — 51П 2а. 2
= 0,
(ез)
Определим значение высоты к = коо, соответствующей максимальному использованию сил сцепления. Очевидно, при этом зт2а=1 и а = 45°. Тогда, полагая 5ш2а = 1 в выражении (е3) и решая его относительно Лэо, получим
к.
2с У
(1У.12)
Таким образом, массив связного грунта может иметь вертикальный откос кдо определенной высоты. При высоте, большей /г90, произойдет сползание призмы аЬс.
Отметим, что в природных условиях грунты обладают не только сцеплением, но и трением, и задача устойчивости откосов становится значительно более сложной, особенно при строгой ее постановке.
Некоторые строгие решения. При строгой постановке задачи для грунтов, обладающих как внутренним трением, так и сцеплением, рассматриваются две основные задачи: 1) определение величины, максимального давления на горизонтальную поверхность массива грунта, при которой откос заданного очертания остается в равновесии, и 2) определение формы равноустойчивого откоса предельной крутизны. Эти задачи получили строгое решение в цитируемых ранее работах чл. корр. АН СССР. проф. В. В. Соколовского (1942; 1954 гг.).
1. Приведем результаты строгого решения первой задачи, полученные на основе численного интегрирования дифференциальных уравнений предельного равновесия при различных углах внутреннего трения ф и разных углах наклона плоского откоса а к горизонту (рис. 76).
Величина предельного давления
пред р = 0гс + р8
и соответствующая координата
с
У = у — -
где о*— значение безразмерного предельного давления
(табл. 21);
ре = с сх§ ф ■— давление связности;
у ■—относительная координата (табл. 21), истинное
"V значение которой у = у —.
Пользуясь данными табл. 21, без труда вычисляются ординаты эпюры предельных давлений на горизонтальную поверхность плоского откоса при любых
Р_«ггттт значениях а, ср, с и у.
2. Форма очертания предельных равноустой-чивых откосов для случая, когда грунт обладает трением и сцеплением,полученная в результате численного решения дифференциальных уравнений предельного равновесия при помощи электронных вычислительных машин, приведена на рис. 77.
Координаты равноустойчивых откосов даны в безразмерных единицах:
с г.
X — х — , У = г/ — ,
у % л;
где х, у — безразмерные координаты по рис. 77.
Очертание равноустойчивого откоса строят начиная с его верхней кромки.
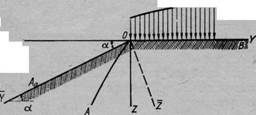
Рис. 76. К определению предельного давления на поверхность плоского откоса
По В. В. Соколовскому, горизонтальная поверхность равноустойчивого откоса может нести равномерно распределенную нагрузку, определяемую выражением
2с соз ср ро = ~-:-■
1 — 81П ф
(1У.13)
Если рассматривать эту нагрузку как давление слоя грунта, полагая рй = ук, то получим
2СС05ф (1У.13')
у(1 — ЗШф)
Для идеально связного грунта (при ф = 0) получим прежнюю формулу (IV. 12):
А = -
V
Метод круглоцилинд-рических поверхностей скольжения широко применяется на практике, так как дает некоторый запас устойчивости и основывается на опытных данных о форме поверхностей скольжения при оползнях вращения, которая на основании многочисленных замеров в натуре (например, Шведской геотехнической комиссии, управления канала Москва — Волга и др.) принимается за круглоци-линдрическую, при этом самое невыгодное ее положение определяется расчетом. Принятие определенной формы поверхностей скольжения и ряда других допущений (о чем будет сказано ниже) делает этот метод приближенным.
-V 36 32
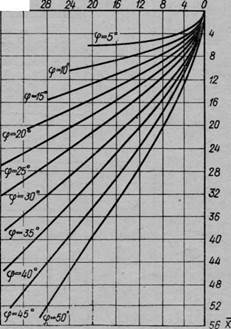
Рис. 77. Форма очертания равноустойчивых откосов
Допустим, что центр круглоцилиндрическои поверхности скольжения оползающей призмы находится в точке О (рис. 78, а). Уравнением равновесия будет ЕУИ0 = 0. Для составления уравнения моментов относительно точки вращения О разбивают призму скольжения АБС вертикальными
Таблица 21
Значения безразмерного предельного давления сь на горизонтальную поверхность откоса
Значения аг при <р, град
| У | ||||||||||||||
| при а, | град | |||||||||||||
| 0,0 | 8,34 | 7,51 | 14,8 | 12,7 | 10,9 | 30,1 | 24,3 | 19,6 | 15,7 | 75,3 | 55,9 | 41,4 | 30,6 | 22,5 |
| 0,5 | 9,02 | 7,90 | 17,9 | 14,8 | 12,0 | 43,0 | 32,6 | 24,4 | 18,1 | 139,0 | 94,0 | 62,6 | 41,3 | 27,1 |
| 1,0 | 9,64 | 8,26 | 20,6 | 16,6 | 13,1 | 53,9 | 39,8 | 28,8 | 20,3 | 193,0 | 126,0 | 81,1 | 50,9 | 31,0 |
| 1,5 | 10,2 | 8,62 | 23,1 | 18,2 | 14,1 | 64,0 | 46,5 | 32,8 | 22,3 | 242,0 | 157,0 | 98,5 | 59,8 | 34,7 |
| 2,0 | 10,8 | 8,95 | 25,4 | 19,9 | 15,0 | 73,6 | 52,9 | 36,7 | 24,2 | 292,0 | 186,0 | 115,0 | 68,4 | 38,1 |
| 2,5 | 11,3 | 9,28 | 27,7 | 21,4 | 15,8 | 82,9 | 59,0 | 40,4 | 26,0 | 339,0 | 215,0 | 132,0 | 76,7 | 41,3 |
| 3,0 | 11,8 | 9,59 | 29,8 | 23,0 | 16,7 | 91,8 | 65,1 | 44,1 | 27,8 | 386,0 | 243,0 | 148,0 | 84,9 | 44,4 |
| 3,5 | 12,3 | 9,89 | 31,9 | 24,4 | 17,5 | 101,0 | 71,0 | 47,6 | 29,4 | 432,0 | 271,0 | 164,0 | 93,0 | 47,5 |
| 4,0 | 12,8 | 10,2 | 34,0 | 25,8 | 18,3 | 109,0 | 76,8 | 51,2 | 31,1 | 478,0 | 299,0 | 179,0 | 101,0 | 50,4 |
| 4,5 | 13,2 | 10,5 | 36,0 | 27,2 | 19,1 | 118,0 | 82,6 | 54,7 | 32,7 | 523,0 | 327,0 | 195,0 | 109,0 | 53,3 |
| 5,0 | 13,7 | 10,8 | 38,0 | 28,7 | 19,9 | 127,0 | 88,3 | 58,1 | 34,3 | 568,0 | 354,0 | 211,0 | 117,0 | 56,2 |
| 5,5 | 14,1 | 11,0 | 39,9 | 20,0 | 20,6 | 135,0 | 94,0 | 61,6 | 35,8 | 613,0 | 381,0 | 226,0 | 125,0 | 59,0 |
| 6,0 | 14,5 | 11,3 | 41,8 | 31,4 | 21,4 | 143,0 | 99,6 | 65,0 | 37,4 | 658,0 | 409,0 | 241,0 | 132,0 | 61,7 |
сечениями на ряд отсеков и принимают вес каждого отсека условно приложенным в точке пересечения веса отсека Рг с соответствующим отрезком дуги скольжения, а силами взаимодействия по вертикальным плоскостям отсека (считая, что давления от соседних отсеков равны по величине, а по направлению прямо противоположны) пренебрегают. Раскладывая далее силы веса Рг на направле-
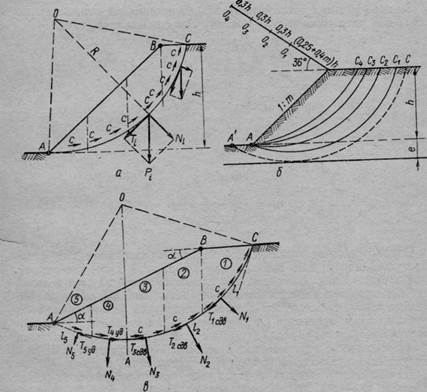
Рис. 78. К расчету устойчивости откоса по круглоцилиндрическим поверхностям скольжения:
а —схема действия сил; б — положение опасных дуг скольжения; в — схема сил, действующих по поверхности скольжения
ние радиуса вращения и ему перпендикулярное, составляют уравнение равновесия, приравнивая нулю момент всех сил относительно точки вращения:
2 ТгР- 2^^^^-сЬР = 0.
Сокращая это выражение на Р, получим
77— ЛМзф —с1 = 0.
(ж.) (ж2)
Здесь Ь — длина дуги скольжения А С; <р, с — угол внутреннего трения и сцепление грунта; 7\уУ,-— составляющие давления от веса отсеков, определяемые графически или вычисляемые по замерам углов йг
(Г* = Рг зш а*; ЛГ< = Рг соз а,).
За коэффициент устойчивости откоса принимают отношение момента сил удерживающих к. моменту сил сдвигающих, т. е.
ИЛИ
2 N4 + сЬ г|==-Э-. (1У.14)
2^
Однако решение поставленной задачи определением коэффициента устойчивости для произвольно выбранной дуги поверхности скольжения не заканчивается, так как необходимо из всех возможных дуг поверхностей скольжения выбрать наиболее опасную. Последнее выполняется путем попыток, задаваясь различными положениями точек вращения О; для уменьшения числа попыток существуют некоторые правила, например, проф. Феллениуса (см. нашу книгу «Механика грунтов», изд. 4), Москва — Волгостроя (рис. 78, б, где указано положение опасных дуг скольжения) и др.
Для ряда намеченных центров дуг поверхностей скольжения (О]; 02; 03 — рис. 78, б) определяют необходимое по условию устойчивости сцепление, соответствующее предельному равновесию заданного откоса по выражению, вытекающему из соотношения (жг), а именно:
с == —:----. (IV. 15)
Далее, из всех возможных центров скольжения выбирают тот, для которого требуется максимальная величина сил сцепления. Этот центр принимается за наиболее опасный и для него по формуле (IV. 14) вычисляется коэффициент устойчивости г).
Обычно считают, что при величине п^ 1,1-=-1,5 откос будет устойчивым.
Формула (IV.14), как показано проф. Г. М. Шахунянцем (1941, 1967 гг.) *, будет справедлива лишь для тех случаев, когда дуга поверхности скольжения во всех своих частях является ниспадающей в сторону возможного смещения откоса или склона или (в случае скольжения по цилиндрической поверхности) когда все отсеки кривой скольжения располагаются по одну сторону от направления вертикального радиуса О А (рис. 78, в).
Если обозначить сдвигающие силы, направленные в сторону скольжения (сдвига), Т{сдв, а сдвигающие силы, направленные в сторону, противоположную направлению смещения (например, Г4 и Т5 по рис. 78, в), и удерживающие откос от скольжения, 7\уд, то формула (IV. 14) примет следующий вид:
2^ + 2^ + 2Г<™
1=1 г=1
(1У.140
2г
г сдв
По выражению (IV. 14') и следует определять коэффициент устойчивости откосов и склонов при расчетах по методу круглоцилин-дрических поверхностей скольжения.
Однако, как показывают соответствующие расчеты, метод круг-лоцилиндрических поверхностей скольжения дает в ряде случаев несколько завышенный запас, а главное — в нем не учитываются усилия, действующие на вертикальные грани отсеков, что делает весь расчет приближенным и вызывает необходимость принятия дополнительных допущений.
Некоторые усовершенствования и упрощения расчетов по методу круглоцилиндрических поверхностей скольжения (введение переменности масштаба, но в прежней постановке задачи) внесены проф. Г. И. Тер-Степаняном и проф. М. Н. Гольдштейном, причем коэффициент устойчивости они рекомендуют определять по выражению
Ц = }А+ — В, (IV. 16)
у/г
где А и В— коэффициенты, зависящие от геометрических размеров сползающего клина, выраженные в долях от высоты откоса к; значения этих коэффициентов по вычислениям М. Н. Гольдштейна приведены в табл. 22.
Определяя из выражения (IV.16) величину к, получим
сВ
й =-—. (IV. 16')
Таблица 22
Значения коэффициентов А и В для приближенного расчета устойчивости откосов
Заложение откоса 1 : т
Поверхность скольжения проходит через нижнюю кромку откоса
Поверхность скольжения проходит через основание и имеет горизонтальную касательную на глубине
| к | |
| а | В |
| 4,32 | 5,80 |
| 4,43 | 5,86 |
| 4,54 | 5,93 |
| 4,66 | 6,00 |
| 4,78 | 6,08 |
| 4,90 | 6,16 |
| 5,08 | 6,26 |
| 5,17 | 6,36 |
| 5,31 | 6,47 |
е=1
1,00 1,25 1,50 1,75 :2,00 :2,25 :2,50 :2,75 :3,00
2,34 2,64 2,64 2,87 3,23 3,19 3,53 3,59 3,59
| 5,79 | 2,56 | 6,10 | 3,17 | 5,92 |
| 6,05 | 2,66 | 6,32 | 3,24 | 6,62 |
| 6,50 | 2,80 | 6,53 | 3,32 | 6,13 |
| 6,58 | 2,93 | 6,72 | 3,41 | 6,26 |
| 6,70 | 3,10 | 6,87 | 3,53 | 6,40 |
| 7,27 | 3,26 | 7,23 | 3,66 | 6,56 |
| 7,30 | 3,46 | 7,62 | 3,82 | 6,74 |
| 8,02 | 3,68 | 8,00 | 4,02 | 6,95 |
| 8,81 | 3,93 | 8,40 | 4,24 | 7,20 |
5,78 5,86 5,94 6,02 6,10 6,18 6,26 6,34 6,44
5,75 5,80 5,85 5,90 5,95 5,98 6,02 6,05 6,09
По формулам (1У.16) и (IV.16') и данным табл. 22 легко вычисляются значения коэффициента устойчивости откоса т) и предельная высота откоса к при принятом коэффициенте устойчивости.
Для грунтов связных с незначительным углом внутреннего трения (при ф<5-=-7°) при залегании на некоторой глубине е плотного грунта (рис. 78, б— дуга поверхности скольжения А'С) расчет производится в предположении выпирания основания за пределами откоса.
Пример 8. Определить предельную высоту откоса с уклоном 1 : 2, если ч=2; Ф = 22°; с=1,2 Т/м2 и у = 1,8 Т/м3. Найдя по табл. 22 значения коэффициентов А я В я подставив их в формулу (1У.16'), будем иметь
сВ
1,2-6,7
1(^-/4)
1,8(2 — 0,404-3,23)
6,4 м.
Оползни скольжения и оползни разжижения. Оползни скольжения имеют место при зафиксированных поверхностях скольжения, например у прислоненных откосов, когда грунты при строительстве укладываются на поверхность уже существующих уплотнившихся откосов земляных сооружений или когда природные склоны или насыпи при нарушении равновесия оползают по фиксированной поверхности скальных или других плотных пород.
Оползни разжижения имеют место в горных областях при катастрофическом выпадении дождей или при весьма быстром таянии снегов. Они представляют собой грязекаменные и водока-менные потоки, которые называются обычно селями.
Сели делятся на связные (структурные) потоки и турбулентные (неструктурные).
Связными (структурными) считают такие селевые потоки, при движении которых не происходит заметного перемешивания оползающих масс в ядре потока. Структурные потоки дают только положительную аккумуляцию и не образуют размывов.
Турбулентные грязекаменные и водокаменные сели, в которых происходит значительное перемешивание грунтовых масс, имеют широкое распространение в горных местностях.
Вопрос о движении селевых потоков рассматривается на базе гидрологических расчетов и теории движения вязких жидкостей, составляя специальную область расчетов, выходящую за рамки курса механики грунтов.
Общий случай расчета устойчивости прислоненных откосов и склонов широко используется при проектировании сооружений на
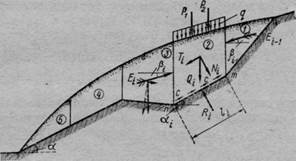
Рис. 79. Схема действия сил при определении оползневого давления
склонах и уширении земляных сооружений: дамб, насыпей и т. п.
Как показано проф. Г. М. Шахунянцем *, коэффициент устойчивости прислоненного массива и в этом случае может быть определен из уравнений равновесия, если разбить массив на ряд отсеков так, чтобы в пределах отдельных отсеков поверхность скольжения была бы плоской и проходила по фиксированной поверхности более плотных ненарушенных пород. Для любых отсеков достаточно просто определяется и так называемое оползневое давление Е{, величина которого необходима для проектирования противооползневых ограждений.
Рассмотрим условие равновесия г'-го отсека (например, второго, рис.79).
Все внешние силы, включая нагрузку, приложенную к поверхности отсека, собственный вес грунта в объеме отсека и пр., приводим к одной равнодействующей С}{. Раскладываем далее равнодействующую внешних сил в ее точке приложения на нормальную N^ и касательную Г, составляющие к фиксированной плоскости скольжения ппг.
Если откос или склон подвержен еще действию сейсмических сил, отклоняющих равнодействующую внешних сил от вертикали на некоторый угол 0,, то получим
Ы{ = С} С05(СХ1 4- 6,) И Тг = <?, 5Ш (щ 4- 9г) . (З1)
При направлении поверхности скольжения пт в сторону возможного сползания отсека значения углов а* берутся со знаком «плюс», так же как и углов 0,-, отклоняющих равнодействующую <2г в сторону сползания.
Заменяем действие соседних (с рассматриваемым) отсеков силами оползневого давления 7^,-1 и Ег (см. рис. 79), направленных под углами Вг-1 и 6г по нормалям к боковым граням отсека. Обозначая далее нормальную составляющую реакции основания отсека пт через /?г- и проектируя все силы на нормаль к основанию отсека и на направление самого отсека, получим
Яг = #, + [Ег ЗШ (ОХ, — Рг) — ЗШ (<Ц — Рг-0 ] ; (Зг)
Тг = Сг/г + ^Яг + [Е{ СОЗ (а* — Рг) — ^г-1 СОЗ (а,- — Рг—1> ] • (Зз)
Подставляя выражение (зг) в (з3) и умножая величину сдвигающей силы 7", на коэффициент устойчивости ц, получим
Т]Гг == Схи 4- \г^г 4- Ех [/г ЗШ (щ — Рг) + СОЗ (<Хг — Рг) ] —
— Ег-1 [/г-1 ЗШ (аг' — Рг-1) + СОЗ (а, — Р,'-1) ] . (з4)
Решая уравнения (з4>) относительно Ег и принимая во внимание,
что
/ = 1§ф и /з1п(а—р) +соз(а — Р): соз (а — р — ф) соз ф
и обозначая составляющую Тг, способствующую сдвигу отсека, через Ггсдв, а удержанию его в равновесии — через ^-уд, получим
Ег =
(г\Тг сдв ~№г — С,7,- — Т^ уд) 003 фг
+ Ег-
С03(аг— рг —фг) СОЗ (а,- — Рг-1 — фг) С03(аг — Рг — фг)
+
(1У.17)
Отметим, что для отсеков, у которых Т{ = ТгСЛВ, в формуле (IV.14') следует значение 7УуД полагать равным нулю.
Вычисления при определении Ег следует начинать с верхнего отсека (7 по рис. 79), для которого /^г_1 = 0.
Для определения коэффициента устойчивости ц свободного откоса или склона проф. Г. М. Шахунянц рекомендует задаваться некоторым его значением т) 1 и определять по формуле (IV. 17) величину оползневого давления для конечного отсека, которую назовем Ек. Если эта величина не равна нулю, то следует задаться другим значением г|2, стремясь получить величину Ек другого знака. Интерполируя далее менаду величинами г|1 и г\2, находят искомое значение т), при котором Ек=0.
Изложенный способ позволяет установить тот отсек (по профилю), где наиболее целесообразно расположить противооползневые подпорные сооружения (в местах наименьших Е{ и не очень большой оползневой толщи), например по рис. 79 в конце третьего отсека.
Если оползневый склон или прислоненный откос будет смещаться как одно целое и контактные силы трения и сцепления между отсеками не будут мобилизованы, то следует положить вг- = 0; в других случаях можно полагать бг- и Вг_1 равными соответствующим углам внутреннего трения грунта.
О мерах борьбы с оползнями. Нарушение устойчивости земляных масс часто сопровождается значительными разрушениями дорог, мостов, жилых и промышленных зданий и других сооружений, а иногда и человеческими жертвами, что вызывает необходимость разрабатывать и осуществлять активные меры борьбы с оползнями и другими нарушениями устойчивости земляных масс.
Меры борьбы с этими нарушениями (оползнями, селями и др.) устанавливаются на основе тщательного изучения природных физико-геологических условий, уяснения основных причин неустойчивости и аналитических расчетов предельного равновесия рассматриваемых массивов грунта.
Основными мерами по увеличению устойчивости массивов грунта и борьбе с оползнями будут:
1) восстановление и усиление естественных упоров оползающих масс (укрепление берегов от размывов, устройство волнобойных сооружений, применение удерживающих подпорных стен, ограждений, направляющих селевые потоки и пр.);
2) регулирование водного режима грунтовых масс (осушение оползневых участков, устройство поверхностного водоотвода и спрямления водотоков, применение глубинного горизонтального и вертикального дренажей и пр.) ;
3) уменьшение градиента нагрузок (уполаживание откосов по расчетам, базирующимся на опытном определении сопротивления грунтов сдвигу; уменьшение внешних нагрузок и пр.).
§ 5. некоторые вопросы теории давления грунтов на ограждения
Вопросы давления грунтов на ограждения являются важнейшими в инженерных расчетах и решаются на базе общей теории предельного напряженного состояния грунтов.
Если свободный откос массива грунта имеет крутизну более предельной (рис. 80), возникает необходимость поддержать его подпорной стенкой.
Вопросам давления грунтов на подпорные стенки посвящено огромное число работ, начиная со времени Кулона (XVIII в.) и до наших дней. Здесь мы ограничимся лишь рассмотрением основных задач по определению давления грунтов на массивные подпорные стенки *.
Как показывают соответствующие исследования, давление грунтов на подпорные стенки зависит не только от свойств грунтов засыпки и изменения этих свойств во времени (уплотнение, релаксация), но и от размеров подпорных стенок и величины возможных перемещений стенок.
В случае податливости основания подпорной стенки происходит поворот ее в сторону от грунта засыпки; при некоторой величине поворота грунт за стенкой приходит в предельное напряженное состоянне, и в области грунта за подпорной стенкой возникают два сопряженных семейства криволинейных поверхностей скольжения.
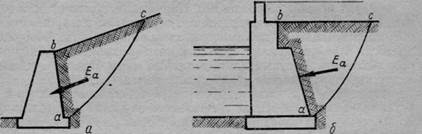
Рис. 80. Некоторые виды подпорных стенок
Задача заключается в определении максимального давления грунта на подпорную стенку, что может быть выполнено математически точно, если известно точное очертание поверхностей скольжения, определяемое решением системы дифференциальных уравнений предельного равновесия [см. формулы (а\)— (аз) § 2 настоящей главы].
Однако в ряде практических приложений без большой погрешности, а для гладких массивных подпорных стенок и точно, можно принять допущение о плоских поверхностях скольжения в грунте за подпорной стенкой со следом плоскости обрушения, проходящим через нижнюю грань стенки.
Сыпучие грунты. При допущении плоских поверхностей скольжения максимальное давление сыпучих грунтов на подпорные стенки определяется исходя из следующих простых соображений.
Любая горизонтальная площадка в грунте за массивной гладкой вертикальной стенкой с горизонтальной поверхностью засыпки испытывает только сжимающее напряжение (нормальное главное напряжение 01), равное весу столба грунта от поверхности до рассматриваемой площадки, т. е.
а{ — уг-1. (щ)
Боковое давление о2 на подпорную стенку найдем из условия, что грунт за стенкой находится в предельном равновесии. Из уравнения предельного равновесия (11.24")
!-*(«•-*)■ «
Принимая во внимание выражение (и,), получим
о2 = у21д2 (45°-|-Х • (IV. 18)
Эпюра распределения давлений по задней грани стенки изобразится треугольником (рис.81).
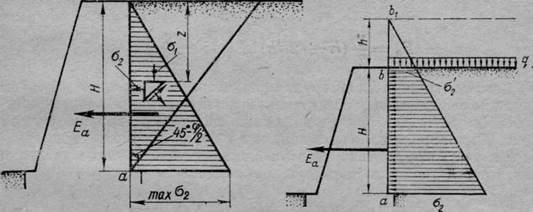
| Рис. 81. Схема действия сил и эпюра бокового давления сыпучего грунта для гладкойподпорной стенки | Рис. 82. Распределение давлений по задней грани стенки при действии равномерно распределенной нагрузки и собственного веса грунта |
Отметим, что для случая, когда стенка будет перемещаться по направлению к грунту (надвигаться на грунт), будет иметь место пассивное сопротивление грунта, знак в скобках формулы (IV. 18) изменится на положительный, и величина пассивного давления будет равна
а2а = уг1^ (450 + -|). ,(1У.18')
Равнодействующая активного давления грунта на подпорную стенку Еа будет равна прощади эпюры давления:
тах а2Н
или
(IV. 19)
Равнодействующая Еа будет горизонтальна и приложена на одной трети высоты от низа подпорной стенки.
В случае действия на поверхность грунта сплошной равномерно распределенной нагрузки д кГ/м2 определяем приведенную высоту слоя грунта Н = ц\у, заменяющую действие нагрузки, продолжаем заднюю грань стенки до пересечения с новой линией засыпки (рис. 82) и строим общую треугольную эпюру давлений.
На подпорную стенку будет действовать только заштрихованная часть эпюры давлений (см. рис. 82). Тогда
_ , а2 + а2 Е& =---п
или
Еа =*|-(№+2ВД8*( 45°-^) .
(1У20)
Связные грунты. Если грунт обладает сцеплением, то заменяем действие сил сцепления всесторонним равномерным давлением связности (ре = с/1§ф), приложенным к свободным граням грунта (рис. 83); приводя далее его действие к эквивалентному слою грунта Н и учитывая противоположно направленное действие давления связности /л, подобно предыдущему получим
02 = у(Я + /г)^( 45°-^-) -р.
или, учитывая,что
п = у!§Ф
И Ре
будем иметь
у у 1§ф ' х 2 ' 1§ф
откуда, произведя несложные преобразования, получим
(К2)
уН (45° - -| Х - 2с 1Ш ( 45° -|- ). (1У.21)
Формулу (IV.21) можно представить в виде
02 = 02ф — 02е,
где
02ф уН1?( 45°-1) ; 02с = 2с 1ё( 45° - -|) .
Таким образом, сцепление уменьшает боковое давление грунта на стенку на постоянную по всей высоте стенки величину 02с. На некоторой глубине Нс суммарное давление будет равно нулю.
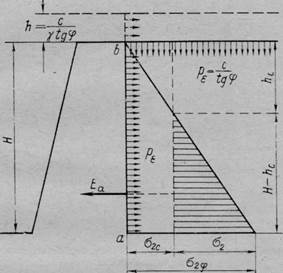
Рис. 83. К определению давления связных грунтов на подпорную стенку
Найдя из условия 02 — 0 глубину Нс, определим величину полного активного давления связного грунта на подпорную стенку как площадь прямоугольного треугольника со сторонами о2 и Я—Нс (рис.83):
^МИ^М (1У.22)
Величину активного давления в рассматриваемом случае можно определить и по формуле (при /гс<Я)
ЕЛ = ^ & (45° - ± ) - 2сЯ 1е (45° -1-) + ^. (1У.22')
Приведем графическое построение, базирующееся на допущении плоских поверхностей скольжения и справедливое для общего случая засыпки грунта за подпорной стенкой, любой формы засыпки и любого наклона задней грани стенки.
Через нижнее ребро А (рис. 84) подпорной стенки проводим несколько возможных плоскостей скольжения — АСи АС2, АС3,... Для каждой из призм обрушения, например призмы АВСЬ строим силовой треугольник, отложив в масштабе от некоторой точки О величину С?!, равную весу призмы АВС\, и проведя линию, параллельную
к.
Т"
АЛ
1.
Рис. 84. Графическое определение максимального давления грунта на подпорную стенку
реакции неподвижной части массива грунта К\, направленной под углом ф к перпендикуляру плоскости скольжения АС\, и линию, параллельную реакции подпорной стенки Е\, направленную под углом трения фо стенки о грунт.
Из условия замыкания силового треугольника по масштабу сил и определим величины Я\ и Е\. Далее, строим силовые треугольники и для призм обрушения АВС2 и АВС3 и т. д., при этом направление реакции подпорной стенки остается неизменным, а направление реакции 7?г- будет меняться в зависимости от угла наклона плоскости скольжения щ.
Построение удобно расположить так, как указано на рис. 84. Из этого построения легко определяется ЕШйх по точке касания прямой, проведенной параллельно <2 к кривой У^Уг^з изменения давления Е. Для получения величины Етах надо провести через найденную точку касания прямую, параллельную направлению Е, и измерить полученный отрезок в масштабе сил.
Значения безразмерных коэффициентов д0 и б (в рад) для определения активного давления грунтов
9 град
| ■ | ||||||||||||
| | | <Р<>1 | град | ||||||||||
| ?0 5 | 0,00 0,00 | 0,00 0,00 | 0,00 0,00 | 0,00 0,00 | 0,00 0,00 | 0,00 0,00 | 0,00 0,00 | 0,00 0,00 | 0,00 0,00 | 0,00 0,00 | 0,00 0,00 | 0,00 0,00 |
| 7о | 0,17 0,00 | 0,17 0,05 | 0,17 0,05 | 0,17 0,00 | 0,17 0,09 | 0,17 0,09 | 0,17 0,00 | 0,17 0,12 | 0,17 0,12 | 0,17 0,00 | 0,17 0,14 | 0,17 0,14 |
| в | 0,34 0,00 | 0,33 0,09 | 0,33 0,10 | 0,33 0,00 | 0,33 0,17 | 0,33 0,17 | 0,32 0,00 | 0,32 0,23 | 0,32 0,23 | 0,32 0,00 | 0,32 0,27 | 0,32 0,27 |
| В | 0,47 0,00 | 0,47 0,09 | 0,47 0,14 | 0,45 0,00 | 0,44 0,17 | 0,45 0,25 | 0,44 0,00 | 0,43 0,26 | 0,44 0,33 | 0,42 0,00 | 0,43 0,35 | 0,44 0,40 |
| ?0 | 0,58 0,00 | 0,57 0,09 | 0,57 0,16 | 0,54 0,00 | 0,52 0,17 | 0,53 0,31 | 0,50 0,00 | 0,48 0,26 | 0,51 0,43 | 0,46 0,00 | 0,47 0,35 | 0,50 0,52 |
| <?0 | 0,67 0,00 | 0,64 0,09 | 0,64 0,17 | 0,59 0,00 | 0,56 0,17 | 0,57 0,34 | 0,52 0,00 | 0,50 0,26 | 0,53 0,49 | 0,46 0,00 | 0,45 0,35 | 0,51 0,62 |
| 9о о | 0,72 0,00 | 0,68 0,09 | 0,68 0,17 | 0,60 0,00 | 0,57 0,17 | 0,57 0,35 | 0,50 0,00 | 0,47 0,26 | 0,50 0,52 | 0,42 0,00 | 0,40 0,35 | 0,46 0,69 |
| <7о 5 | 0,73 0,00 | 0,70 0,09 | 0,70 0,17 | 0,58 0,00 | 0,54 0,17 | 0,54 0,35 | 0,46 0,00 | 0,43 0,26 | 0,45 0,52 | 0,35 0,00 | 0,34 0,35 | 0,38 0,70 |
| <7о | 0,72 0,00 | 0,70 0,09 | 0,68 0,17 | 0,54 0,00 | 0,50 0,17 | 0,50 0,35 | 0,40 0,00 | 0,37 0,26 | 0,38 0,52 | 0,29 0,00 | 0,27 0,35 | 0,29 0,70 |
| <7о 5 | 0,70 0,00 | 0,67 0,09 | 0,65 0,17 | 0,49 0,00 | 0,45 0,17 | 0,44 0,35 | 0,33 0,00 | 0,30 0,26 | 0,31 0,52 | 0,22 0,00 | 0,20 0,35 | 0,22 0,70 |
| <7о | 0,65 0,00 | 0,61 0,09 | 0,59 0,17 | 0,42 0,00 | 0,38 0,17 | 0,37 0,35 | 0,26 0,00 | 0,24 0,26 | 0,24 0,52 | 0,16 0,00 | 0,14 0,35 | 0,15 0,70 |
| 7о ? | 0,58 0,00 | 0,54 0,09 | 0,52 0,17 | 0,35 0,00 | 0,31 0,17 | 0,30 0,35 | 0,20 0,00 | 0,18 0,26 | 0,17 0,52 | 0,11 0,00 | 0,09 0,35 | 0,10 0,70 |
| 7о | 0,49 0,00 | 0,45 0,09 | 0,44 0,17 | 0,27 0,00 | 0,24 0,17 | 0,23 0,35 | 0,13 0,00 | 0,12 0,26 | 0,11 0,52 | 0,06 0,00 | 0,05 0,35 | 0,05 0,70 |
Примечание. В— угол, составляемый задней гранью стенки с горизонтом, отсчитываемый от задней грани стенки по часовой стрелке; ф, (ро—угол внутреннего трения грунта и угол трения грунта о стенку; 6 — угол, составляемый давлением грунта с нормалью к задней грани стенки (для крутых стенок, близкий к (р),
Так как величина суммарного давления на подпорную стенку равна площади треугольной эпюры боковых давлений, то удельное давление у нижнего ребра задней грани стенки будет равно
тахгт2 =-(1У.23)
Я
где Я —длина задней грани подпорной стенки.
В заключение настоящего параграфа приведем результаты строгого решения (проф. В. В. Соколовского) задачи об активном давлении сыпучего грунта на подпорные стенки, полученные путем численного интегрирования преобразованных нелинейных дифференциальных уравнений теории предельного равновесия методом конечных разностей (табл. 23).
Величина активного давления вычисляется по формуле
- о-2 = до(уг + <7), (1У.24)
где ц — интенсивность равномерно распределенной нагрузки на горизонтальную поверхность засыпки;
до — безразмерный коэффициент (табл. 23).
Дата добавления: 2016-06-02; просмотров: 2942;
