Величины максимальных сжимающих напряжений (в долях от р) в слое грунта на несжимаемом основании под ленточным фундаментом
При залегании несжимаемого слоя на глубине
к=Ь,
Й-2»,
1,0 0,8 0,6 0,4 0,2 0,1
1,000 1,009 1,020 1,024 1,023 1,022
1,00 1,99 0,92 0,84 0,78 0,76
1,00 0,82 0,57 0,44 0,37 0,36
Примечание. В таблице обозначено: Н — мощность сжимаемого слоя (до скальной породы); Ь\ — полуширина равномерно распределенной полосообразной нагрузки; г — координата центра площадки, для которой определяется напряжение (при начале координат всегда на границе между сжимаемым слоем и жестким основанием).
По данным этой таблицы на рис. 58 построены эпюры распределения сжимающих напряжений, по оси полосообразной нагрузки для случаев залегания несжимаемой скальной породы на глубине, равной полуширине 1, ширине 1' и 2,5 ширины 1" ленточной нагрузки. На том же рисунке изображена эпюра 2 максимальных сжимающих напряжений для случая однородного полупространства (без наличия скального подстилающего слоя) и распределение тех же напряжений 3, 3', 3" в случае более неоднородного подстилающего слоя с переменным модулем деформируемости, когда
| Р «Г/СМ2 | ||||
| ни \ | \\\\\ | |||
| ь, | . Р | |||
| з ,4 ж | Г | |||
| 2Ь, | '/////// // / / | У Г | УУУ///У | |
| у/ууууг зь, | 1 1 1II | ///////. | ||
| 46-, | •з" ' \' / ( | г | -2 | |
| 56, | / 1 1 } , ,1, 1 | |||
| 5Ь, |
Рис. 58. Эпюры распределения максимальных сжимающих напряжений под центром гибкой равномерно нагруженной полосы в слое грунта ограниченной толщины:
; — при наличии -иодстилающей несжимаемой породы; 2 —для однородного полупространства; 3—для неоднородного слоя с возрастающей по глубине сжимаемостью грунта
он, уменьшаясь по глубине, на нижней границе слоя в несколько раз меньше модуля деформируемости у подошвы нагрузки (по нашим и В. Д. Пономарева данным).
Из рассмотрения эпюр распределения сжимающих напряжений (давлений) вытекает, что наличие жесткого несжимаемого слоя вызывает концентрацию (возрастание) напряжений по оси нагрузки, тогда как увеличение сжимаемости грунта с глубиной уменьшает концентрацию напряжений.
Распределение контактных давлений для слоя грунта ограниченной толщины, опирающегося на несжимаемое основание, для жестких фундаментов приведено (по вычислениям НИИ оснований) в табл. 15.
Таблица 15
Величины контактных давлений под жестким фундаментом на слое грунта ограниченной толщины в долях от р
| ПИ | Мощность слоя при Н\Я | или й/й. | |||||
| или | |||||||
| №1 | 0,25 | 6,5 | 10 и более |
Для круглого фундамента
| 0,0 | 0,905 | 0,829 | 0,652 | 0,532 | 0,509 | 0,503 | 0,500 |
| 0,1 | 0,904 | 0,828 | 0,652 | 0,535 | 0,512 | 0,505 | 0,503 |
| 0,2 | 0,904 | 0,823 | 0,654 | 0,541 | 0,519 | 0,513 | 0,511 |
| 0,3 | 0,902 | 0,817 | 0,658 | 0,533 | 0,532 | 0,527 | 0,525 |
| 0,4 | 0,900 | 0,809 | 0,665 | 0,572 | 0,553 | 0,548 | 0,546 |
| 0,5 | 0,896 | 0,802 | 0,678 | 0,600 | 0,584 | 0,579 | 0,578 |
| 0,6 | 0,891 | 0,798 | 0,700 | 0,642 | 0,630 | 0,627 | 0,626 |
| 0,7 | 0,886 | 0,804 | 0,744 | 0,712 | 0,704 | 0,702 | 0,701 |
| 0,8 | 0,889 | 0,841 | 0,833 | 0,834 | 0,834 | 0,833 | 0,833 |
| 0,9 | 0,945 | 0,985 | 1,073 | 1,131 | 1,143 | 1,147 | 1,146 |
| 0,95 | 1,093 | 1,252 | 1,446 | 1,565 | 1,589 | 1,600 | 1,599 |
Для ленточного фундамента
| 0,0 | 0,949 | 0,915 | 0,811 | 0,705 | 0,699 | 0,649 |
| 0,1 | 0,948 | 0,914 | 0,811 | 0,707 | 0,672 | 0,652 |
| 0,2 | 0,948 | 0,909 | 0,811 | 0,714 | 0,680 | 0,661 |
| 0,3 | 0,946 | 0,903 | 0,813 | 0,725 | 0,695 | 0,678 |
| 0,4 | 0,942 | 0,895 | 0,818 | 0,744 | 0,719 | 0,704 |
| 0,5 | 0,938 | 0,889 | 0,826 | 0,773 | 0,753 | 0,743 |
| 0,6 | 0,932 | 0,884 | 0,846 | 0,818 | 0,806 | 0,800 |
| 0,7 | 0,927 | 0,891 | 0,885 | 0,891 | 0,891 | 0,892 |
| 0,8 | 0,932 | 0,924 | 0,972 | 1,029 | 1,046 | 1,055 |
| 0,9 | 0,998 | 1,071 | 1,220 | 1,366 | 1,413 | 1,443 |
| 0,95 | 1,161 | 1,343 | 1,618 | 1,869 | 1,954 | 2,010 |
Для фундаментов гибких приведем табл. 16 для определения контактных давлений на слое грунта ограниченной толщины под действием полосообразной нагрузки интенсивностью р, вычисленную Гидропроектом (Г. В. Крашенинниковой и др., 1961 г.) при допущении отсутствия трения по контакту упругого слоя с несжимаемым основанием по методу ступенчатого суммирования Б. Н. Жемочки-на (рис. 59) *. В этой таблице значения реактивных давлений даны для пяти различных мощностей слоя грунта ограниченной толщины в зависимости от гибкости фундаментной балки Г, определяемой выражением
Г ж 10-=^-, ЕМ
где / — полупролет балки (см. рис. 59);
Е0 — модуль общей деформации слоя грунта;
Е\ — модуль упругости материала фундаментной балки;
Нх — высота прямоугольной фундаментной балки.
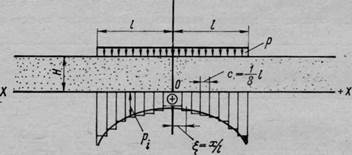
Рис. 59. Эпюра реактивных давлений по подошве гибкого фундамента на слое грунта ограниченной толщины
Так же как и в ранее рассмотренных случаях, если известны реактивные давления, то расчетные величины для фундаментной балки шах М и тах С} определяются по уравнениям статики.
Распределение напряжений от собственного веса грунта. Напряжения от собственного веса грунта, так называемые природные (или «бытовые», что менее употребительно) давления, имеют значение для свеженасыпных земляных сооружений и оценки природной уплотненности грунтов.
При горизонтальной поверхности грунта напряжения от собственного веса грунта (с объемным весом у2) будут увеличиваться с глубиной 2 и равны
о"г = | Угйг; Ох = оу = ^оСг; о
Тгу — Тгх — 0,
где |0 = ——--коэффициент бокового давления грунта в сос-
1 — ро
тоянии покоя.
Таблица 16
Значения реактивных давлений в долях от р, осредненных на участках длиной с=1/8/, для полупролета / гибких равномерно нагруженных балок на слое грунта ограниченной толщины Н
| Г-0 | г-з | |||||||||||||
| при Н, рапном | ||||||||||||||
| г/16 | г/4 | 1/2 | г | гг | оо | г/16 | г/4 | г/2 | г | 2г | - | |||
| 1/16 3/16 5/16 7/16 9/16 11/16 13/16 15/16 | | | 0,970 0,972 0,976 0,966 0,956 0,946 0,960 1,254 | 0,924 0,925 0,929 0,918 0,910 0,911 0,927 1,556 | 0,828 0,829 0,836 0,837 0,857 0,899 0,987 1,927 | 0,718 0,725 0,741 0,769 0,816 0,909 1,059 2,263 | 0,639 0,640 0,668 0,710 0,770 0,874 1,070 2,629 | 0,996 1,002 1,002 0,998 1,001 1,001 1,000 1,000 | 0,990 0,985 0,980 0,975 0,960 0,960 0,960 1,190 | 0,958 0,956 0,954 0,934 0,916 0,904 0,904 1,474 | 0,876 0,874 0,874 0,866 0,870 0,893 0,956 1,791 | 0,786 0,789 0,796 0,808 0,836 0,899 1,013 2,073 | 0,733 0,738 0,751 0,772 0,814 0,898 1,043 2,251 | ||
| Продолжение табл. 16 | ||||||||||||||
| /■-» | Г- | ■ 5 | ||||||||||||
| при Н, равном | ||||||||||||||
| г/16 | г/4 | г/2 | г | гг | оо | г/16 | г/4 | г/2 | г | гг | оо | |||
| 1/16 3/16 5/16 7/16 9/16 11/16 13/16 15/16 | | | 1,004 1,006 1,008 0,962 1,008 1,006 1,004 1,002 | 0,990 0,988 0,988 0,965 0,960 0,960 0,970 1,179 | 0,972 0,969 0,964 0,942 0,919 0,901 0,895 1,438 | 0,900 0,895 0,892 0,879 0,877 0,890 0,946 1,720 | 0,820 0,819 0,821 0,826 0,845 0,895 0,992 1,989 | 0,773 0,775 0,781 0,794 0,824 0,893 1,018 2,142 | 1,030 1,032 1,036 1,027 1,037 1,023 1,016 1,004 | 1,018 1,010 1,008 0,920 0,980 0,980 0,970 1,114 | 0,994 0,989 0,981 0,953 0,925 0,898 0,881 1,380 | 0,938 0,931 0,923 0,902 0,889 0,887 0,915 1,615 | 0,875 0,871 0,866 0,859 0,862 0,889 0,955 1,822 | 0,889 0,858 0,821 0,742 0,842 0,870 0,980 1,988 |
Следует отметить, что выражения для боковых давлений ах и ау будут справедливы только при горизонтальной поверхности грунта и могут меняться в зависимости от рельефа местности, горообразовательных процессов и пр., что, однако, можно установить лишь путем специальных натурных испытаний.
При постоянном объемном весе напряжения
02 = уг.
Для грунтовой же массы (т. е-, для полностью водонасыщенных грунтов с наличием свободной гидравлически непрерывной воды) величина сжимающих напряжений будет
02 = у'г,
где у' — объемный вес грунта с учетом взвешивающего действия воды; определяется по формуле (1.8) или (1.8').
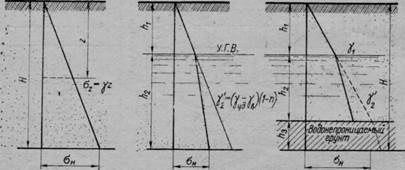
На рис. 60 показано несколько эпюр распределения вертикальных давлений от собственного веса грунта.
а • 5 6
Рис. 60. Распределение давлений от собственного веса грунта:
с — однородный грунт; 6 — при наличии (на глубине Л|) уровня грунтовых вод; в — при наличии под грунтовыми водами (на глубине /*! + А2) водонепроницаемой породы
Некоторые общие выводы. Из всего изложенного в этой главе следует, что в настоящее время в механике грунтов имеет широкое применение теория линейно деформируемых тел. Учет нелинейной зависимости между деформациями и напряжениями производится лишь в особых случаях.
Возникает, однако, вопрос — насколько решения теории линейно деформируемых тел отвечают результатам непосредственных измерений?
Следует здесь же отметить, что задача измерения напряжений (или хотя бы только давлений) внутри массива грунта является технически очень сложной, так как внесение в грунт инородного тела (измерителя напряжений) может изменить напряженное состояние в рассматриваемом месте. Исследования, однако, показывают, что измерять, например, давления в грунте можно лишь специальными очень жесткими дисковыми месдозами, заранее про-градуированными в аналогичных условиях.
Хотя по распределению давлений в грунтах под нагрузкой проведено очень много опытов, только малое число их удовлетворяет современным требованиям.
Отсылая интересующихся этим вопросом лиц к литературе и материалу, приведенному в нашей книге «Механика грунтов» изд. 4, 1963 г., остановимся здесь лишь на самых общих выводах.
Сравнивая результаты опытов (Г. И. Покровского и И. С. Федорова, Н. А. Цытовича и Д. С. Баранова, Г. Пресса, С. Я. Эдель-мана и др.) с расчетными величинами, полученными по теории линейно деформируемых тел, приходим к выводу, что как по характеру, так и по абсолютной величине расчетные данные близки к замеренным, если строго соблюдены граничные условия и измерения проведены в фазе линейной зависимости между напряжениями и деформациями. Здесь, однако, следует отдавать предпочтение результатам наблюдений над реальными сооружениями по сравнению с опытами с малыми площадками загрузки.
Так, например, вопрос о распределении контактных давлений (который раньше вызывал много дискуссий) на основании как некоторых прежних опытов (например, М. Бургера, С. С. Вялова, А. Г. Родштейна и др.), так и новейших обобщений (В. А. Флорина, 1959 г., Э. Шульца, 1965 г. и др.), дает вполне определенное решение, а именно: характер распределения контактных давлений по подошве фундаментов (седлообразный или параболический) определяется не видом того или иного грунта, а гибкостью фундамента и степенью развития пластических деформаций в грунтовом основании, зависящей как от величины удельной нагрузки на грунт, так и глубины заложения (боковой пригрузки) фундаментов, а также площади передачи нагрузки.
Как правило, во всех случаях (за исключением лишь незаглуб-ленных фундаментов на рыхлых грунтах) в фазе линейной деформируемости следует принимать седлообразное распределение давлений по подошве фундамента с учетом влияния граничных условий (ограниченности слоя сжимаемого грунта и т. п.).
Глава IV
Дата добавления: 2016-06-02; просмотров: 1497;
