Определение сжимающих напряжений по методу угловых точек.
Знание величины сжимающих напряжений для угловых точек под прямоугольной площадью загрузки позволяет очень быстро вычислять сжимающие напряжения для любой точки полупространства, особенно если пользоваться значениями угловых коэффициентов Кс (табл.9).
Для площадок под центром загруженного прямоугольника сжимающее напряжение ах0 будет равно
СГгО
Кор
(Ш.7)
Т а б л и Ц а 9
Значения коэффициентов / и /' [формулы (111.9) и (111.10)]
| Прямоугольные фундаменты с отношением сторон а=,//* | ||||||||||||
| р | п га | 1,2 | 1,6 | 1,8 | 2,4 | 2,8 | 3,2 | |||||
| 0,0 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
| 0,4 | 0,949 | 0,960 | 0,968 | 0,972 | 0,974 | 0,975 | 0,976 | 0,976 | 0,977 | 0,977 | 0,977 | 0,977 |
| 0,8 | 0,756 | 0,800 | 0,830 | 0,848 | 0,859 | 0,866 | 0,870 | 0,875 | ' 0,878 | 0,879 | 0,880 | 0,881 |
| 1,2 | 0,547 | 0,606 | 0,652 | 0,682 | 0,703 | 0,717 | 0,727 | 0,740 | 0,746 | 0,749 | 0,753 | 0,754 |
| 1,6 | 0,390 | 0,449 | 0,496 | 0,532 | 0,558 | 0,578 | 0,593 | 0,612 | 0,623 | 0,630 | 0,639 | 0,639 |
| 2,0 | 0,285 | 0,336 | 0,379 | 0,414 | 0,441 | 0,463 | 0,481 | 0,505 | 0,520 | 0,529 | 0,540 | 0,545 |
| 2,4 | 0,214 | 0,257 | 0,294 | 0,325 | 0,352 | 0,374 | 0,392 | 0,419 | 0,437 | 0,449 | 0,462 | 0,470 |
| 2,8 | 0,165 | 0,201 | 0,232 | 0,260 | 0,284 | 0,304 | 0,321 | 0,350 | 0,369 | 0,383 | 0,400 | 0,410 |
| 3,2 | 0,130 | 0,160 | 0,187 | 0,210 | 0,232 | 0,251 | 0,267 | 0,294 | 0,314 | 0,329 | 0,348 | 0,360 |
| 3,6 | 0,106 | 0,130 | 0,153 | 0,173 | 0,192 | 0,209 | 0,224 | 0,250 ■ | 0,270 | 0,285 | 0,305 | 0,320 |
| 4,0 | 0,087 | 0,108 | 0,127 | 0,145 | 0,161 | 0,176 | 0,190 | 0,214 | 0,233 | 0,248 | 0,270 | 0,285 |
| 4,4 | 0,073 | 0,091 | 0,107 | 0,122 | 0,137 | 0,150 | 0,163 | 0,185 | 0,203 | 0,218 | 0,239 | 0,256 |
| 4,8 | 0,062 | 0,077 | 0,092 | 0,105 | 0,118 | 0,130 | 0,141 | 0,161 | 0,178 | 0,192 | 0,213 | 0,230 |
| 5,2 | 0,053 | 0,066 | 0,079 | 0,091 | 0,102 | 0,112 | 0,123 | 0,141 | 0,157 | 0,170 | 0,191 | 0,208 |
| 5,6 | 0,046 | 0,058 | 0,069 | 0,079 | 0,089 | 0,099 | 0,108 | 0,124 | 0,139 | 0,152 | 0,172 | 0,189 |
| 6,0 | 0,040 | 0,051 | 0,060 | 0,070 | 0,078 | 0,087 | 0,095 | 0,110 | 0,124 | 0,136 | 0,155 | 0,172 |
| 6,4 | 0,036 | 0,045 | 0,053 | 0,062 | 0,070 | 0,077 | 0,085 | 0,098 | 0,111 | 0,122 | 0,141 | 0,158 |
| 6,8 | 0,032 | 0,040 | 0,048 | 0,055 | 0,062 | 0,069 | 0,076 | 0,088 | 0,100 | 0,110 | 0,128 | 0,144 |
| 7,2 | 0,028 | 0,036 | 0,042 | 0,049 | 0,056 | 0,062 | 0,068 | 0,080 | 0,090 | 0,100 | 0,117 | 0,133 |
| 7,6 | 0,024 | 0,032 | 0,038 | 0,044 | 0,050 | 0,056 | 0,062 | 0,072 | 0,082 | 0,091 | 0,107 | 0,123 |
| 8,0 | 0,022 | 0,029 | 0,035 | 0,040 | 0,046 | 0,051 | 0,056 | 0,066 | 0,075 | 0,084 | 0,098 | 0,113 |
| 8,4 | 0,021 | 0,026 | 0,032 | 0,037 | 0,042 | 0,046 | 0,051 | 0,060 | 0,069 | 0,077 | 0,091 | 0,105 |
| 8,8 | 0,019 | 0,024 | 0,029 | 0,034 | 0,038 | 0,042 | 0,047 | 0,055 | 0,063 | 0,070 | 0,084 | 0,098 |
| 9,2 | 0,018 | 0,022 | 0,026 | 0,031 | 0,035 | 0,039 | 0,043 | 0,051 | 0,058 | 0,065 | 0,078 | 0,091 |
| 9,6 | 0,016 | 0,020 | 0,024 | 0,028 | 0,032 | 0,036 | 0,040 | 0,047 | 0,054 | 0,060 | 0,072 | 0,085 |
| 0,015 | 0,019 | 0,022 | 0,026 | 0,030 | о.озз | 0,037 | 0,044 | 0,050 | 0,056 | 0,067 | 0,079 | |
| 0,011 | 0,017 | 0,020 | 0,023 | 0,027 | 0,029 | 0,033 | 0,040 | 0,044 | 0,050 | 0,060 | 0,071 | |
| 0,009 | 0,015 | 0,018 | 0,020 | 0,024 | 0,026 | 0,028 | 0,034 | 0,038 | 0,044 | 0,051 | 0,060 |
(В к **
1,000 0,977 0,881 0,755 0,642 0,550 0,477 0,420 0,374 0,337 0,306 0,280 0,258 0,239 0,223 0,208 0,196 0,184 0,175 0,166 0,158 0,150 0,144 0,137 0,132 0,126 0,114 0,104
Примечание. Для промежуточных значений а и величины коэффициентов определяются интерполяцией.
и для площадок под углом загруженного прямоугольника
Огс = КсР, (Ш.8)
где Д'о и Д'с — табличные коэффициенты;
р— интенсивность равномерно распределенной нагрузки.
Значения коэффициентов Ко и Кс определяются по табл. 9 как функции относительной глубины $=2г/Ь или $=г/Ь (по СНиПу — т) и соотношения сторон прямоугольной площади загрузки (а = = Щ (по СНиПу — п):
/22 / \
*-/(Т.Т)-. (НИ)
1 /2 / \
(111.10)
Последние выражения позволяют пользоваться одной таблицей как при вычислении коэффициентов для центральных точек Ко, так и для угловых Кс-
Значения угловых коэффициентов Квс=\" 1/Ь) ■ {1 + цо) для суммы главных напряжений приведены в табл. 10.
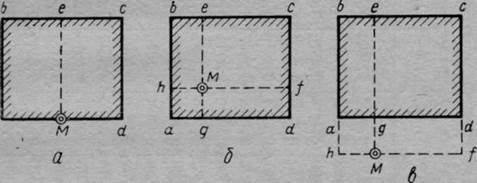
Рис. 44. Схема разбивки прямоугольной площади загрузки при
определении напряжений по методу угловых точек
Максимальное сжимающее напряжение макс аг будет в точках, расположенных под центром загруженной площади, и вычисляется по формуле (Ш.7).
Метод угловых точек для определения величины сжимающих напряжений ах применяется тогда, когда грузовая площадь может быть разбита на такие прямоугольники, чтобы рассматриваемая точка оказалась бы угловой. Тогда сжимающее напряжение в этой точке (для горизонтальных площадок, параллельных плоской границе полупространства) будет равно алгебраической сумме напряжений от прямоугольных площадей загрузки, для которых эта точка является угловой.
Поясним сказанное, рассмотрев три основных случая:
1) точка М находится на контуре прямоугольника внешних давлений (рис. 44, а);
2) точка М — внутри прямоугольника давлений (рис. 44, б);
3) точка М — вне прямоугольника давлений (рис. 44, в).
Таблица 10
Значения вс /(1 + д0) в точках на разных глубинах, расположенных на угловых вертикалях при равномерно распределенной
по прямоугольной площади нагрузке р в долях от р
| 2 * | |||||||||||||||
| 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 3,0 | 4,0 | 6,0 | 8,0 | 10,0 | |
| 0,0 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 |
| 0,2 | 0,2439 | 0,3405 | 0,3804 | 0,4003 | 0,4114 | 0,4183 | 0,4230 | 0,4259 | 0,4281 | 0,4297 | 0,4337 | 0,4352 | 0,4363 | 0,4367 | 0,4369 |
| 0,4 | 0,1363 | 0,2280 | 0,2810 | 0,3119 | 0,3308 | 0,3430 | 0,3515 | 0,3570 | 0,3612 | 0,3643 | 0,3721 | 0,3750 | 0,3771 | 0,3779 | 0,3782 |
| 0,6 | 0,0874 | 0,1578 | 0,2074 | 0,2406 | 0,2630 | 0,2782 | 0,2890 | 0,2967 | 0,3024 | 0,3068 | 0,3179 | 0,3222 | 0,3454 | 0,3265 | 0,3270 |
| 0,8 | 0,0607 | 0,1136 | 0,1552 | 0,1812 | 0,2087 | 0,2251 | 0,2371 | 0,2458 | 0,2529 | 0,2582 | 0,2721 | 0,2776 | 0,2818 | 0,2833 | 0,2840 |
| 1,0 | 0,0443 | 0,0846 | 0,1185 | 0,1456 | 0,1667 | 0,1828 | 0,1952 | 0,2047 | 0,2121 | 0,2180 | 0,2341 | 0,2406 | 0,2457 | 0,2476 | 0,2486 |
| 1,2 | 0,0336 | 0,0649 | 0,0924 | 0,1156 | 0,1344 | 0,1495 | 0,1616 | 0,1711 | 0,1788 | 0,1850 | 0,2026 | 0,2101 | 6,2162 | 0,2182 | 0,2193 |
| 1,4 | 0,0262 | 0,0510 | 0,0735 | 0,0931 | 0,1097 | 0,1235 | 0,1348 | 0,1441 | 0,1518 | 0,1580 | 0,1766 | 0,1848 | 0,1915 | 0,1940 | 0,1952 |
| 1,6 | 0,0209 | 0,0410 | 0,0596 | 0,0762 | 0,0906 | 0,1030 | 0,1135 | 0,1223 | 0,1296 | 0,1358 | 0,1549 | 0,1638 | 0,1711 | 0,1739 | 0,1753 |
| 1,8 | 0,0171 | 0,0336 | 0,0491 | 0,0632 | 0,0758 | 0,0868 | 0,0964 | 0,1046 | 0,1116 | 0,1177 | 0,1368 | 0,1460 | 0,1540 | 0,1571 | 0,1588 |
| 2,0 | 0,0142 | 0,0280 | 0,0410 | 0,0531 | 0,0641 | 0,0739 | 0,0826 | 0,0900 | 0,0967 | 0,1024 | 0,1214 | 0,1310 | 0,1395 | 0,1428 | 0,1445 |
| 2,5 | 0,0094 | 0,0187 | 0,0276 | 0,0361 | 0,0440 | 0,0514 | 0,0581 | 0,0642 | 0,0696 | 0,0745 | 0,0921 | 0,1020 | 0,1114 | 0,1153 | 0,1173 |
| 3,0 | 0,0067 | 0,0133 | 0,0198 | 0,0260 | 0,0319 | 0,0375 | 0,0427 | 0,0475 | 0,0520 | 0,0561 | 0,0718 | 0,0814 | 0,0913 | 0,0957 | 0,0980 |
| 5,0 | 0,0025 | 0,0050 | 0,0074 | 0,0099 | 0,0122 | 0,0146 | 0,0168 | 0,0190 | 0,0212 | 0,0232 | 0,0322 | 0,0391 | 0,0481 | 0,0532 | 0,0561 |
| 7,0 | 0,0013 | 0,0026 | 0,0038 | 0,0051 | 0,0064 | 0,0076 | 0,0088 | 0,0100 | 0,0111 | 0,0124 | 0,0177 | 0,0224 | 0,0293 | 0,0339 | 0,0370 |
| 10,0 | 0,0006 | 0,0013 | 0,0019 | 0,0025 | 0,0032 | 0,0038 | 0,0044 | 0,0047 | 0,0056 | 0,0067 | 0,0091 | 0,0118 | 0,0163 | 0,0198 | 0,0224 |
Примечания: Ь — ширина загруженного прямоугольника в плоскости чертежа; / — длина в направлении, перпендикулярном плоскости чертежа.
В первом случае величина а2 определится как сумма двух угловых напряжений, соответствующих прямоугольникам загрузки МаЬе и Меси, т. е.
СТг == (/Сю + /Сгс) р,
где Л'1с и /\"2с— угловые коэффициенты, определяемые по формуле (111.10) и данным табл. 9 в зависимости от относительной глубины р = г/й и отношения сторон сх ==ЦЪ;
р — интенсивность внешней равномерно распределенной нагрузки.
Во втором случае необходимо суммировать угловые напряжения от четырех прямоугольных площадей загрузки: МдаН, МНЬе, Мес\ и М\Лц. т. е.
аг = (/Сю + Кгс + /Сзс + Кь)р.
В третьем случае напряжение в точке М складывается из суммы напряжений от действия нагрузки по прямоугольникам МНЬе и Мес\, взятых со знаком «плюс», и напряжений от действия нагрузки по прямоугольникам МИа@ и М§с1{, взятых со знаком «минус», т. е.
Ох = (/Сю + Кгс — Кзс — /С4с) р,
где /Сю, /Сгс, /Сзс, /Сю — угловые коэффициенты, определяемые по формуле (111.10) и табл. 9 в зависимости от соответствующих величин а = 11Ь и $ = г/Ь.
Для облегчения расчетов в табл. 11 приведены заранее вычисленные более подробные значения угловых коэффициентов Кс' = = {"'(г1Ь, 1/Ь), позволяющие обходиться без формулы (111.10), используя лишь выражение (П1.8), т. е.
огс = Кар-
(Ш.8')
Пример 2. Определить величину сжимающих напряжений под центром и под серединой длинной стороны загруженного прямоугольника размером 2x8 м на глубине 2 м от поверхности при внешней нагрузке интенсивностью р = 3 кГ/см2,
Для площадки под центром загруженной площади
2г 2-2 . /8
*=2*р=—=т=2;а=т=т=4-
По табл. 9 коэффициент Ко = 0,54; тогда
аг0 = К0р = 0,54-3 = 1,62 кГ1см*.
Для. площадки под серединой длинной стороны прямоугольной площадки загрузки, разделяя ее на два прямоугольника размером 4x2 м, так чтобы рассматриваемая точка была бы угловой, 2 = 2 м; р = г/Ь=1;
Ь 2
V -
Интеополируя по табл. 9, по формуле (ШЛО) получим
1_ 0,870 + 0,727 4 ' 2
■ 0.2:
а2 = 2КсР = 2-0,2-3= 1,20 кГ\см2.
Значения коэффициента Кс
Таблица
Значения а=1;Ь
1,2
1,4
1,8
2,2
2,4
2,6
0,2500 0,2486 0,2401 0,2229 0,1999 0,1752 0,1516 0,1308 0,1123 0,0969 0,0840 0,0732 0,0642 0,0566 0,0502 0,0447 0,0401 0,0361 0,0326 0,0296 0,0270 0,0247 0,0227 0,0209 0,0193 0,0179 0,0127 0,0094 0,0073 0,0058 0.0047
0,2500 0,2489 0,2420 0,2275 0,2075 0,1851 0,1626 0,1423 0,1241 0,1083 0,0947 0,0832 0,0734 0,0651 0,0580 0,0519 0,0467 0,0421 0,0382 0,0348 0,0318 0,0291 0,0268 0,0247 0,0229 0,0212 0,0151 0,0112 0,0087 0,0069 0,0056
0,2500 0,2490 О,2429 0,2300 0,2120 0,1911 0,1705 О,1508 0,1329 0,1172 0,1034 0,0917 0,0813 0,0725 0,0649 0,0583 0,0526 0,0477 0,0433 0,0395 0,0362 0,0333 0,0306 0,0283 0,0262 0,0243 0,0174 0,0130 0,0101 0,0080 0.0065
0,2500 0,2491 0,2434 0,2315 0,2147 0,1955 О,1758 О,1569 0,1396 0,1241 0,1103 0,0984 0,0879 0,0788 0,0709 0,0640 0,0580 0,0527 0,0480 0,0439 0,0403 0,0371 0,0343 0,0317 0,0294 0,0274 0,0196 0,0147 0,0114 0,0091 0,0074
О,2500 0,2491 0,2437 0,2324 0,2165 0,1981 0,1793 0,1613 0,1445 О,1294 0,1158 0,1039 0,0934 0,0842 0,0761 0,0690 0,0627 0,0571 0,0523 0,0479 0,0441 0,0407 0,0376 0,0348 0,0324 0,0302 0,0218 0,0161 0,0127 0,0102 0,0083
0,2500 0,2491 0,2439 0,2329 0,2176 0,1999 0,1818 0,1644 0,1482 0,1334 0,1202 0,1084 0,0979 0,0887 0,0805 0,0732 0,0668 0,0611 0,0561 0,0516 0,0474 0,0439 0,0407 О,0378 0,0352 О,0328 0,0238 0,0180 0,0140 0,0112 0,0092
0,2500 0,2492 0,2440 0,2333 0,2183 0,2012 0,1836 0,1667 0,1509 0,1365 0,1236 0,1120 0,1016 0,0924 0,0842 0,0769 0,0704 0,0646 0,0594 0,0548 0,0507 0,0469 0,0436 0,0405 0,0378 0,0353 0,0257 0,0195 0,0153 0,0122 0,0100
),2500 ),2492 1,2441 ),2335 ),2188 1,2020 1,1849 1,1685 1,1530 1,1389 ),1263 ),1149 ),1047 1,0955 ),0875 ),0801 ),0735 1,0677 ),0624 ),0577 1,0535 1,0496 1,0462 ),0430 1,0402 1,0376 1,0276 1,0210 1,0165 1,0132 1,0109
0,2500 0,2492 0,2442 0,2337 0,2192 0,2026 0,1858 0,1696 0,1545 0,1408 0,1284 0,1172 0,1071 0,0981 0,0900 0,0828 0,0762 0,0704 0,0651 0,0603 0,0560 0,0521 0,0485 0,0453 0,0424 0,0397 0,0293 0,0224 0,0176 0,0142 0,0117
0,2500 0,2492 0,2442 0,2338 0,2194 0,2031 0,1865 0,1705 0,1557 0,1423 0,1300 0,1191 0,1092 0,1003 0,0923 0,0851 0,0786 0,0727 0,0674 0,0626 0,0588 0,0543 0,0507 0,0474 0,0444 0,0417 0,0310 0,0238 0,0187 0,0152 0,0125
0,2500 0,2492 0,2442 0,2339 0,2196 0,2034 0,1870 0,1712 0,1567 0,1434 0,1314 0,1205 0,1108 0,1020 0,0942 0,0870 0,0806 0,0747 0,0694 0,0646 0,0603 0,0563 0,0527 0,0493 0,0463 0,0435 0,0325 0,0251 0,0198 0,0161 0,0132
Продолжение табл. И
| Значения | а- ЦЬ | ||||||||||||
| 9-- | |||||||||||||
| ь | 3,2 | 3,4 | 3,6 , | 3,8 | |||||||||
| 0,0 | 0,2500 | 0,2500 | 0,2500 | 0,2500 | 0,2500 | 0,2500 | 0,2500 | 0,2500 | 0,2500 | ||||
| 0,2 | 0,2492 | 0,2492 | 0,2492 | 0,2492 | 0,2492 | 0,2492 | 0,2492 | 0,2492 | 0,2492 | ||||
| 0,4 | 0,2443 | 0,2443 | 0,2443 | 0,2443 | 0,2443 | 0,2443 | 0,2443 | 0,2443 | 0,2443 | ||||
| 0,6 | 0,2340 | 0,2340 | 0,2341 | 0,2341 | 0,2341 | 0,2342 | 0,2342 | 0,2342 | 0,2342 | ||||
| 0,8 | 0,2198 | 0,2199 | 0,2199 | 0,2200 | 0,2200 | 0,2202 | 0,2202 | 0,2202 | 0,2202 | ||||
| 1,0 | 0,2037 | 0,2039 | 0,2040 | 0,2041 | 0,2042 | 0,2044 | 0,2045 | 0,2046 | 0,2046 | ||||
| 1,2 | 0,1873 | 0,1876 | 0,1878 | 0,1880 | 0,1882 | 0,1885 | 0,1888 | 0,1888 | 0,1888 | ||||
| 1,4 | 0,1718 | 0,1722 | 0,1725 | 0,1728 | 0,1730 | 0,1735 | 0,1739 | 0,1739 | 0,1740 | ||||
| 1,6 | 0,1574 | 0,1580 | 0,1584 | 0,1587 | 0,1590 | 0,1598 | 0,1602 | 0,1604 | 0,1604 | ||||
| 1,8 | 0,1443 | 0,1450 | 0,1455 | 0,1460 | 0,1463 | 0,1474 | 0,1480 | 0,1482 | 0,1482 | ||||
| 2,0 | 0,1324 | 0,1332 | 0,1339 | 0,1345 | 0,1350 | 0,1363 | 0,1371 | 0,1373 | 0,1374 | ||||
| 2,2 | 0,1218 | 0,1227 | 0,1235 | 0,1242 | 0,1248 | 0,1264 | 0,1274 | 0,1277 | 0,1277 | ||||
| 2,4 2,6 | 0,1122 | 0,1133 | 0,1142 | 0,1150 | 0,1156 | 0,1175 | 0,1188 | 0,1191 | 0,1192 | ||||
| 0,1035 | 0,1047 | 0,1058 | 0,1066 | 0,1073 | 0,1095 | 0,1111 | 0,1115 | 0,1116 | |||||
| 2,8 | 0,0957 | 0,0970 | 0,0982 | 0,0991 | 0,0999 | 0,1024 | 0,1041 | 0,1047 | 0,1048 | ||||
| 3,0 | 0,0887 | 0,0901 | 0,0913 | 0,0923 | 0,0931 | 0,0959 | 0,0980 | 0,0986 | 0,0987 | ||||
| 3,2 | 0,0823 | 0,0838 | 0,0850 | 0,0861 | 0,0870 | 0,0900 | 0,0923 | 0,0930 | 0,0933 | ||||
| 3,4 | 0,0765 | 0,0780 | 0,0793 | 0,0804 | 0,0814 | 0,0847 | 0,0873 | 0,0880 | 0,0882 | ||||
| 3,6 | 0,0712 | 0,0728 | 0,0741 | 0,0753 | 0,0763 | 0,0799 | 0,0826 | 0,0835 | 0,0837 | ||||
| 3,8 | 0,0664 | 0,0680 | 0,0694 | 0,0706 | 0,0717 | 0,0753 | 0,0784 | 0,0794 | 0,0796 | ||||
| 4,0 | 0,0620 | 0,0636 | 0,0650 | 0,0663 | 0,0674 | 0,0712 | 0,0745 | 0,0756 | 0,0758 | ||||
| 4,2 | 0,0581 | 0,0596 | 0,0610 | 0,0623 | 0,0634 | 0,0674 | 0,0709 | 0,0721 | 0,0724 | ||||
| 4,4 | 0,0544 | 0,0560 | 0,0574 | 0,0586 | 0,0597 | 0,0639 | 0,0676 | 0,0689 | 0,0692 | ||||
| 4,6 | 0,0510 | 0,0526 | 0,0540 | 0,0553 | 0,0564 | 0,0606 | 0,0644 | 0,0659 | 0,0663 | ||||
| 4,8 | 0,0480 | 0,0495 | 0,0509 | 0,0522 | 0,0533 | 0,0576 | 0,0616 | 0,0631 | 0,0635 | ||||
| 0,0451 | 0,0466 | 0,0480 | 0,0493 | 0,0504 | 0,0547 | 0,0589 | 0,0606 | 0,0610 | |||||
| 0,0340 | 0,0353 | 0,0366 | 0,0377 | 0,0388 | 0,0431 | 0,0479 | 0,0500 | 0,0506 | |||||
| 0,0263 | 0,0275 | 0,0286 | 0,0296 | 0,0306 | 0,0346 | 0,0396 | 0,0421 | 0,0428 | |||||
| 0,0209 | 0,0219 | 0,0228 | 0,0237 | 0,0246 | 0,0283 | 0,0332 | 0,0359 | 0,0367 | |||||
| 0,0169 | 0,0178 | 0,0186 | 0,0194 | 0,0202 | 0,0235 | 0,0282 | 0,0310 | 0,0319 | |||||
| 0,0140 | 0,0147 | 0,0154 | 0,0162 | 0,0167 | 0,0198 | 0,0242 | 0,0270 | 0,0280 |
Влияние площади загрузки. Расчеты напряжений в грунтах показывают, что чем больше площадь передачи нагрузки, тем медленнее происходит затухание (рассеивание на большую площадь) напряжений с глубиной. Это и понятно, так как согласно рис. 45, а, если добавить к нагрузке 7 некоторую нагрузку 2 или 3, то в точке М сжимающее напряжение сг увеличится, но в меньшей степени, чем от нагрузки 1, так как расстояние Р до точки М также увеличится, а с увеличением расстояния величина добавочных напряжений уменьшается.
2*8м Мм
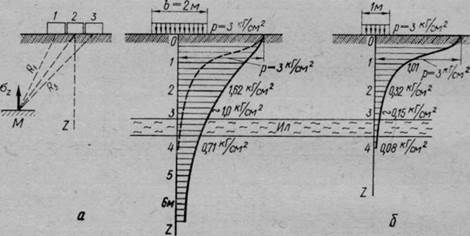
Рис. 45. Пример влияния размеров загруженной площади на распределение сжимающих напряжений по глубине
Возрастание напряжений с увеличением площади можно установить непосредственно и по данным табл. 9 и проиллюстрировать следующими примерами.
Так, в примере 2 было получено, что на глубине 2 м от ограничивающей полупространство плоскости давление от действия внешней нагрузки интенсивностью р = 3 кГ/см2, распределенной по площади 2X8 ж2, равнялось а2=1,62 кГ/см2. Если при той же интенсивности внешняя нагрузка на поверхность грунта будет действовать по площадке 1X1 м2, то сжимающее напряжение на той же глубине 2 м, учитывая, что в этом случае
2г 2•2 I
$ = — = — = 4; а = — =1; Ко = 0,108 Ь 1 Ь
будет равно
о-г = /С0р = 0,108-3 = 0,32 кГ/см\
На рис. 45, б приведены эпюры распределения сжимающих напряжений по оси нагрузки для двух нагруженных площадей: 2X8 м2 и 1 X 1 м2.
Как видно из приведенных эпюр, при одном и том же внешнем давлении на поверхности напряжения по глубине сильно отличаются, завися от величины площади загрузки.
Таким образом, внешние давления тем медленнее загасают с глубиной, чем больше площадь загрузки, и на любой заданной глубине сжимающие напряжения будут тем больше, чем больше площадь загрузки. Последнее имеет существенное практическое значение. Так, например, слабые слои грунта при большой площади загрузки на некоторой глубине могут испытывать очень большие давления (больше их несущей способности), тогда как при малых площадях загрузки возникающие давления совершенно не повлияют на прочность и устойчивость даже слабого грунта, так как они будут малы по величине. В приведенном на рис. 45, б примере на глубине 3 м от загруженной поверхности под площадкой 2X8 м давление будет около 1,0 кГ/см2, тогда как под площадкой 1X1 м на той же глубине — всего лишь около 0,15 кГ/см2.
Способ элементарного суммирования. Для площадей загрузки сложной формы, которые нельзя разделить на прямоугольники (например, имеющих криволинейное очертание в плане или составленных из треугольников и более сложных фигур), метод угловых точек неприменим.
В этом случае пользуются способом элементарного суммирования, который заключается в следующем. Загрузочную площадь разделяют на площадки таких размеров, чтобы можно было считать приходящиеся на них нагрузки сосредоточенными в их центрах тяжести.
Путем сравнения с результатами точного решения установлено, что при разделении нагруженной поверхности на элементы, длинная сторона которых /о меньше половины расстояния от центра элемента Но до точки, в которой определяется сжимающее напряжение,
/о 1
погрешность составляет около 6%, т. е. при — < — погрешность
АО 2
1о 1 10 1
л ^ 6%. Точно так же при — ^ — ц ^ 3% и при — ^ — л.^2%.
АО 3 АО 4
Приведенные данные вводят определенность в расчеты сжимающих напряжений по способу элементарного суммирования.
Следует, однако, отметить, что способ элементарного суммирования непригоден для определения главных напряжений, а в ряде случаев (например, при расчете влияния на осадки соседних фундаментов) требуется учет горизонтальных напряжений.
Сжимающее напряжение по способу элементарного суммирования определяется по формуле (111.4), суммируя напряжения от элементарных загрузочных площадок:
ЙХП р
^=2Кг—(Ш.4") г=1
| 2 м | Р «г/смг | ||
| 1м 1 /М | т | шщ |
где К, — коэффициент, определяемый по табл. 8 в зависимости от отношения гг/г (здесь гг — проекция на горизонтальную площадь расстояния от центра тяжести /-го элемента до рассматриваемой точки; г — глубина);
и — число элементов.
Пример 3. Определить величину сжимающего напряжения с* для горизонтальной площадки, расположенной по оси, проходящей через центр 0 прямоугольной части загруженной площадки (рис.-46), и лежащей на глубине 2 ж от поверхности, при действии равномерно распределенной нагрузки интенсивностью р = 3 кГ/см2.
Разбиваем загруженную площадь на 6 элементов: четыре квадрата размером 1X1 м и 2 прямоугольных треугольника с катетами в 1 м.
Принимаем, что в центре каждого элемента приложена сосредоточенная сила Рг = рР{ (где Р\— площадь элемента). Так как в рассматриваемом примере отношение наибольшего измерения любого элемента /0 к расстоянию до рассматриваемой точки % будет меньше двух, то погрешность определения стг по формуле (111.44") будет меньше 6% (в сторону увеличения напряжения).
Определим расстояния по горизонтали от принятых точек приложения сосредоточенных сил (центров тяжести элементов) до вертикальной оси, проходящей через рассматриваемую точку, т. е. величины п (рис. 46):
для квадратных элементов г> = г2 = г3 = гА = = Т~2?2 = 0,71 ж;
для треугольных элементов ''5 = ''б =

Рис. 46. К примеру определения сжимающих напряжений по способу элементарного суммирования
при
при
/-!_4 0,71 г = 2
&д 1,37
= 0,355
=1' 1,332 + 0,332=1,37 ж.
Тогда, интерполируя по табл. 8, определяем следующее:
К\ = 0,3549 и
= 0,685
Тогда
К2 = 0,1850.
= 4Л',
^1 2-2
+ 2Л':
^1
или, подставляя значения К\ и Л"2, а также ^1=30 Т и ^2=15 Т, получим
1,2 кГ:см?.
30 000 15 000
= , = 4-0,3549--+ 2-0,1850-
200-200
200-200
При желании более точного определения величины сжимающих напряжений необходимо разбивать грузовую площадь на меньшие элементы. Точно таким же путем можно определить величину сжимающих напряжений и для любой другой точки линейно деформируемого полупространства.
Дата добавления: 2016-06-02; просмотров: 3297;
