Общая зависимость между деформациями и напряжениями.

Рассмотрим общий случай зависимости относительной деформации е от величины нормального напряжения а для грунта в целом. Такое рассмотрение будет полностью справедливо для начального и конечного состояния грунта, когда отсутствует перераспределение фаз в единице объема грунта '(например, когда при уплотнении за­кончится выдавливание воды из пор грунта). При рассмотрении промежуточных состояний необходимо учитывать процесс консоли­дации, ползучесть скелета и пр.

При анализе зависимости деформаций от напряжений следует различать по крайней мере два вида грунтов: сыпучие и связные.

Для сыпучих грунтов при однократном загружении всегда возникают необратимые смещения и повороты зерен грунта относи­тельно друг друга, что обусловливает постоянное наличие остаточ­ных деформаций.

Для связных грунтов на характер деформирования сущест­венно влияют структурные сзязи —как жесткие, так и вязкие. При жестких связях, если величина нагрузки такова, что при ее действии прочность связей не нарушается, грунт будет деформироваться как квазитвердое тело.

При вязких (водно-коллоидных) связях в грунтах некоторые связи начинают разрушаться (или вязко течь) уже при весьма не­больших усилиях, другие — при несколько больших и т. д., что и обусловливает и у этих грунтов постоянное наличие при разгрузке не только обратимых, но и остаточных деформаций. Важно отме­тить, что остаточные деформации часто во много раз превосходят по величине деформации обратимые. *

Природные связные грунты в большинстве случаев имеют и же­сткие, и чисто вязкие связи различной прочности, поэтому процесс деформирования их является весьма сложным. Условия возникно­вения того или иного вида деформаций грунтов (упругих, остаточ­ных уплотнения, вязкого течения, ползучести и др.), а также мето­ды их определения будут подробно рассмотрены в гл. V и VI. Здесь мы лишь остановимся на рассмотрении общей зависимости между относительными деформациями е и нормальным напряжением с. так как эта зависимость кладется в основу теории распределения напряжений в грунтах и определения их деформаций под действием внешних сил.

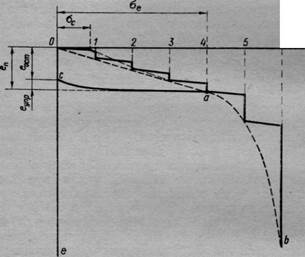
Рис. 35. Зависимость между деформациями е и

нормаль­ными напряжениями а для грунтов

при ступенчатом возрастании нагрузки

В самом общем случае, как показывают многочисленные иссле­дования, зависимость между деформациями и напряжениями для грунтов будет нелинейной (рис. 35, пунктирная кривая ОаЬ). Эту зависимость в общем виде можно представить функцией

е = асос + аа(аа— ос)т, (11.35)

где ссс и ап — коэффициенты, определяемые опытным путем;

вс — напряжение, не превосходящее начальной проч­ности структурных связей (сгс^/7Стр);

(<Тд—Ос) =0 — действующее нормальное напряжение, обуслов­ливающее деформации грунта при частичном или полном нарушении структурных связей;

т — параметр нелинейности, также определяемый опытным путем.

Величина коэффициента ас может быть принята равной обрат­ной величине модуля нормальной упругости грунта Е, т. е.

Е

Что касается значения коэффициента ап, то природа его значи­тельно сложней. Если рассматривать только стабилизированные напряжения, то величина этого коэффициента будет зависеть от мо­дуля общей деформации Е0 грунта [см. формулу (11.37)], который в общем случае может входить в выражение в некоторой степени/", меньшей или равной единице, а также от коэффициента р, оценива­ющего способность бокового расширения грунта (определение вели­чины (3 дано в гл. V), т. е. можно принять

Р

о(г) •

где параметр также определяется опытным путем.

Если рассматривать деформации грунта при давлениях, боль­ших структурной прочности сжатия, то зависимости (11.35) можно придать следующий вид:

е =* ас.пОт, (11.35')

где ас.п — некоторый общий коэффициент пропорциональности, в простейшем случае равный ас.п = Р/-Ео.

Общая зависимость (11.35') даже в представленной простой фор­ме еще очень сложна для применения на практике.

Принцип линейной деформируемости. При не очень больших из­менениях внешних давлений (порядка 1—3 кГ/см2, а для плотных и твердых грунтов и до 5—7 кГ/см2) с достаточной для практиче­ских целей точностью зависимость между деформациями е и напря­жениями о может приниматься линейной (см. спрямленный учас­ток Оа на кривой рис. 35), что значительно упрощает расчеты и не вносит в них недопустимых погрешностей. Полагая в выражении (11.35') величину параметра от=1 (что вполне допустимо при вели­чине напряжений, меньших практического предела пропорциональ­ности), между общими деформациями и напряжением ае при посто­янстве модуля общей деформации будем иметь

е = ас.по-, (11.36)

т. е. при небольших изменениях напряжений к грунтам с полным к тому основанием можно применять теорию линейно деформируемых тел.

Как показано проф. Н. М. Герсевановым (1931 г.), если зависи­мость между общими деформациями и напряжениями линейна, то для определения напряжений в грунтах полностью будут примени­мы решения теории упругости; для определения же общих дефор­маций грунтов необходимы добавочные условия (например, зави­симость изменения коэффициента пористости от давления и др.).

Изложенное позволяет сформулировать для грунтов так называемый принцип линейной деформируемости, а именно:

при небольших изменениях давлений можно рассматривать грунты как линейно деформируемые тела, т. е. с достаточной для практических целей точностью можно принимать зависимость между общими деформациями и напряжениями для грунтов линейной.

Этот принцип вытекает также и из рассмотренного случая сжа­тия слоя грунта при сплошной нагрузке (компрессии грунта) в диапазоне давлений, при котором справедлив закон уплотнения. Действительно, по формуле (II.5') имеем

5»

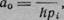
а так как относительная деформация

то

\е = аоР1. \ (11.36')

Сравнивая далее выражение (11.36) с выражением (11.36') и принимая во внимание, что в рассматриваемом случае

Р

о = р и ас.п = —,

•Со

получим

а0 = -^ (П.37)

или

Е0 = -, (П.37')

а0

где Е₀ - модуль общей деформации грунта, определяемый по фор­муле (11.27), используя результаты испытаний образцов грунта на трехосное сжатие или данные полевых опытов пробной нагрузкой.

Коэффициент р, как указывалось ранее, зависит от коэффици­ента относительной поперечной деформации грунта (аналогичного коэффициенту Пуассона для упругих тел) и приблизительно равен: для песков р = 0,8; для супесей р = 0,7; для суглинков р = 0,5 и для глин р = 0,4 (см. гл. V).

Следует отметить, что принцип линейной деформируемости грун­тов (справедливый для грунтов средней уплотненности при давле­ниях порядка 1—3 кГ/см2 и несколько более) является одним из основных в современной механике грунтов, так как на нем базиру­ются почти все инженерные расчеты напряжений и деформаций естественных грунтовых оснований. Для слабых же грунтов (при несущей способности их, меньшей 1 кГ/см2) необходимо исходить из нелинейной зависимости между деформациями и напряжениями.

Деформируемость отдельных фаз грунта. Напряженно-деформи­рованное состояние скелета грунта, а также однокомпонентных и квазиоднофазных грунтов (т. е. грунтов, у которых при деформиро­вании соотношение фаз в единице объема практически не меняется) будет строго описываться уравнениями (11.35) и (11.36) лишь при ^ = 0 и / = оо, т. е. когда процесс перераспределения фаз грунта в единице объема не начался или уже закончился; для промежуточ­ных же отрезков времени напряженно-деформированное состояние грунтов, вообще говоря, будет зависеть от времени I.

Как показывают новейшие исследования, изменения во времени напряженно-деформированного состояния скелета грунта (а также однокомпонентных и однофазных грунтов в целом) являются ре­зультатом реологических свойств скелета грунта — его ползучести при нагрузке.

Опытами С. Р. Месчяна и других подтверждено положение В. А. Флорина о том, что деформируемость скелета дисперсных грунтов (при закончившемся процессе консолидации) вполне описы­вается линейной (в отношении напряжений) теорией наследствен­ной ползучести Больцмана — Вольтерра.

Согласно этой теории в самом общем случае относительная де­формация скелета грунта е(1) (или квазиоднокомпонентных грун­тов в целом) определяется выражениями:

при однократном загружении в течение А^о напряжением ст(/о)

е({) = ^- + К((-и)а{и)М0 (И.38)

■С мгн

и при непрерывном загружении

е(0 = -^-[ог(0+ "К{1-и)о{и)йи , (11.38')

■С мгн д

где К(1—(о) —так называемое ядро ползучести, характеризующее скорость ползучести при постоянном напряжении, отнесенную к еди­нице действующего давления, причем К(1—1<>)=К(1—1о)/Ештн.

Уравнения (11.38) и (11.38') показывают, что полная относитель­ная деформация скелета грунта зависит не только от напряженного состояния за время, прошедшее от начала загружения, но и от пре­дыдущей истории нагружения (/0), почему и теория получила назва­ние теории наследственной ползучести.

Следует также отметить, что уравнения (11.38) и (11.38') спра­ведливы при любом ядре ползучести.

Простейший вид ядра ползучести, хорошо подтверждаемый для дисперсных глинистых грунтов непосредственными опытами, имеет вид

К(1-и) = бе-в'Сг-Ч (11.39)

где б и 61 — параметры ползучести, определяемые опытным путем.

Деформируемость поровой воды в случае полного отсутствия в ней пузырьков газа невелика; в этом случае вода может рассматри­ваться как идеально упругое тело. Полностью дегазированная вода характеризуется значительным

3*

модулем упругости — порядка 20 000 кГ/см².

Совсем иное дело — поровая вода, содержащая замкнутые пу­зырьки воздуха и растворенные газы (а в природе почти любая по­ровая вода содержит некоторое количество газов); она обладает значительной деформируемостью, которую необходимо учитывать в ряде расчетов.

Учет объемной сжимаемости газосодержащей поровой воды су­щественно влияет на величину и протекание во времени деформа­ций-водонасыщенных грунтов (фильтрационных и ползучести), что будет рассмотрено в гл. V и VI.

Можно показать *, что величина коэффициента объемной сжи­маемости газосодержащей поровой жидкости аю при незначитель­ном содержании газов (менее 2% от объема пор) определяется сле­дующим простым выражением:

а» ~ (1 -/в)—■, (П.40)

где /в коэффициент водонасыщенности грунта [см. формулу (1.6')];

ра — величина атмосферного давления, кГ/см2.

Что касается деформируемости самих замкнутых пузырьков воздуха (третьей фазы грунтов), то она обычно отдельно не учиты­вается в расчетах, так как замкнутые пузырьки воздуха окружены жидкостью и движутся и деформируются вместе с ней, а свободный воздух не воспринимает никакого давления. Однако, как было изло­жено выше, деформируемость смеси воздух — вода должна учиты­ваться в полной мере.

Таким образом, в самом общем случае при исследовании на­пряженно-деформированного состояния грунтов следует учитывать деформируемость всех фаз грунта в их взаимодействии, особенно если рассматривается изменение напряженно-деформированного состояния грунтов во времени. Вопрос упрощается лишь для на­чального момента времени и стабилизированного состояния, для ко­торых, как указывалось ранее, полностью будет применимо про­стейшее выражение принципа линейной деформируемости [выраже­ние (11.36')]. При исследовании же напряженно-деформированного состояния грунтов во времени необходимо для водонасыщенных грунтов рассматривать изменения эффективных напряжений в про­цессе фильтрационной консолидации, а для вязких глинистых грун­тов— влияние на напряженно-деформированное состояние ползуче­сти скелета грунта во взаимодействии с фильтрационным процессом уплотнения. Для грунтов неводонасыщенных при /в^0,85 и для квазиоднофазяых грунтов изменение напряженно-деформированно­го состояния во времени будет зависеть исключительно от ползуче­сти скелета грунта.