Распределение напряжений в случае пространственной задачи
Действие сосредоточенной силы (основная задача). Рассмотрим действие сосредоточенной силы Р, приложенной перпендикулярно к ограничивающей полупространство плоскости (рис. 39). Будем считать полупространство однородным в глубину и в стороны и линейно деформируемым.
Задача будет заключаться в определении всех составляющих
чхх, тжг/) а также перемещений и)х, хюи, шх для любой точки полупространства, имеющей координаты г, у, х или /? и р.
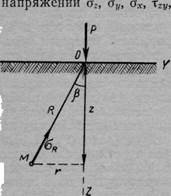
Рис. 39. Схема действия сосредоточенной силы
Поставленная задача для упругого (а следовательно, и любого линейно деформируемого) полупространства впервые была полностью решена проф. Ж. Буссинеском (1885 г.), а определение напряжений для площадок, параллельных ограничивающей полупространство плоскости — проф. В. Кирпичевым и автором книги (1923—1934 гг.). Здесь мы ограничимся выводом только формул напряжений для площадок, параллельных ограничивающей плоскости, как наиболее часто используемых в расчетной практике, т. е. напряжений ах, хгу и ггх.
Возьмем точку М (рис. 39), определяемую полярными координатами р и |3, и определим величину нормального напряжения Од, действующего по направлению радиуса Р, а затем по формулам перехода — и все составляющие напряжения для площадки, проведенной через точку М, параллельно ограничивающей плоскости.
Для упрощения вывода (окончательный результат которого полностью совпадает с решением Буссинеска) примем как постулат, что напряжение ан пропорционально соз р и обратно пропорционально квадрату расстояния от точки приложения сосредоточенной силы Р2.
Следует отметить, что, как показано Проктором и Мораном на 1 Международном конгрессе по механике грунтов (1936 г.), зто положение может быть выведено строго и. из закона всемирного тяготения Ньютона.
Таким образом, полагаем
°* = Л_ (м)
где А — некоторый коэффициент, определяемый из условия равновесия.
Для составления равновесия проведем полушаровое сечение с центром в точке приложения сосредоточенной силы (рис. 40). Величина напряжений, нормальных к иолушаровой поверхности, определяется выражением (м) и будет изменяться от нуля у ограничивающей плоскости до максимума по оси 2, но для выделенного элементарного шарового пояса с центральным углом йр может приниматься постоянной.
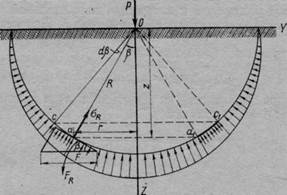
Рис. 40. Схема радиальных напряжений при
действии сосредоточенной силы
Условием равновесия будет: сумма проекций всех сил на вертикальную ось равна нулю:
я/2
Р— | Он С08 $йР = 0, (н)
о
где йР — поверхность элементарного шарового пояса, равная
йР = 2п{Р йшр) (Я<*р).
Подставляя выражение для йР и ся в уравнение (н), получим
я/2
Р — А2к " соз2 р зш рс(р == 0. (п)
о
Произведя интегрирование и подставляя пределы, получим
/>_|_ЛЯ = 0, (р)
откуда неизвестный коэффициент пропорциональности А равен
2 л
Подставляя полученное значение А в формулу (м), для радиальных напряжений будем иметь
3 Р
Отнесем величину радиальных напряжений не к площадке, перпендикулярной радиусу, а к площадке, параллельной ограничивающей плоскости и составляющей с ней угол р. Назовем это напряжение Он'.
Из геометрических соотношений
0"н = ОН С05 Р
или, подставляя значение ок из выражения (т) и принимая во вни мание, что соз $ = г/Р, получим
3 Р 22
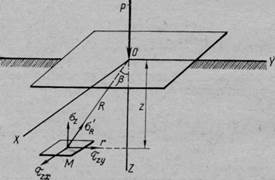
Рис. 41. Составляющие напряжений для площадки,
параллельной ограничивающей плоскости
Далее, не меняя направления площадки, разложим силу оц'Р (рис. 41) на три направления: одно 7. — перпендикулярное площадке и два X и У — лежащих в плоскости площадки. Тогда

А так как СО5(0К', 2)=г/Р; С08(ал', У)=у1Я и со5(0Л', X) =х/Я, то величины составляющих напряжений для площадки, параллельной ограничивающей плоскости, окончательно будут иметь следующий вид:
Ох
| р | ||
| ~2 | я | *р7 |
| Р | г/22 | |
| 2* | я | Ж |
| р | Х22 | |
| У | я | Ж |
(Ш.1)
Отметим, что величины как сжимающих ог, так и сдвигающих тгг/ и хгх напряжений для площадок, параллельных ограничивающей полупространство плоскости, не зависят от упругих постоянных полупространства; тогда как для других площадок, параллельных ограничивающим Плоскостям Х02 и У02, они будут зависеть от модулей деформируемости Е0, р0 и определяются более сложными выражениями*.
Приведем здесь выражения для вычисления суммы нормальных напряжений 9 в любой точке и перемещений иог ограничивающей поверхности, параллельной оси 2:
Р г
@ = Ог + Оу+Ох= (Т1+ СГ2+ 03 = — (1 + Ро)—. Д1И.2) (Ш.З)
Р3
где Сш2 пСЯ— так называемый коэффициент линейно деформируемого полупространства (Е0 — модуль общей деформации, р0—■ коэффициент относительной поперечной деформации, аналогичный коэффициенту Пуассона).
Формулы (III.2) и (111.3) имеют большое практическое значение в расчетах осадок фундаментов.
Выражению для величины сжимающих напряжений ох можно придать более простой вид, позволяющий составить вспомогательную таблицу, облегчающую вычисления напряжений.
Согласно рис. 41 точка М вполне определяется двумя ее координатами 2 и г. Принимая во внимание, что
Р = у22 + Г2 _ г
ИНТ.
из первой строки формулы (III.1) получаем
Р
или, обозначив
2л
будем иметь
| Г | / г V1 | |
| 2я 1 + | ||
| ■ | \ 2 ' а | |
ог = /С-
(П1.4)
Формула (Ш.4) широко используется на практике при расчете осадок фундаментов. Для облегчения расчетов служит табл. 8 значений коэффициента К в формуле для вертикальных сжимающих напряжений в массиве /> р, грунта, нормальных к площадкам, .параллельным ограничивающей полупространство плоскости. Величина коэффициента К определяется для ряда значений г/г (где г — расстояние по горизонтали от оси г, проходящей через точку приложения сосредоточенной силы, а г — глубина рассматриваемой точки от ограничивающей плоскости).
Если на поверхности массива приложено несколько сосредоточенных сил Р\, Р2, Рз ••• (рис. 42), то сжимающее напряжение в любой точке массива для горизонтальных площадок, параллельных ограничивающей плоскости, найдется простым суммированием, так как вывод формулы (1П.4) основан на прямой пропорциональности между напряжениями и деформациями:
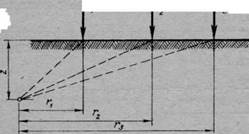
Рис. 42. Схема действия нескольких сосредоточенных сил
А1—+ Л2—,+ Лз —,
(Ш.4')
где коэффициенты К% определяются из табл. 8 в зависимости от соответствующих отношений /ч/г.
Пример 1. На плоскую поверхность массива грунта приложена сосредоточенная сила Я=60 Т. Определить вертикальное сжимающее напряжение в точке а, расположенной на глубине 2 м от поверхности и на расстоянии 1 ж в сторону от линии действия силы (рис. 43).
Для точки а имеем: 2=200 см; г= 100 см; /-/2=0,5. По табл. 8, отношению г/г=0,5 соответствует К=0,2733. По формуле (Ш.4)
Р 60 000
^ = /(— = 0,2733-^^ = 0,41 к Г [ем2.
Точно таким же путем определены сжимающие напряжения для ряда площадок, расположенных на той же глубине 2 = 2 ж и на других глубинах по оси 2. По результатам вычислений построены эпюры сжимающих напряжений для сечения на глубине 2=2 м и для горизонтальных площадок по вертикальной оси
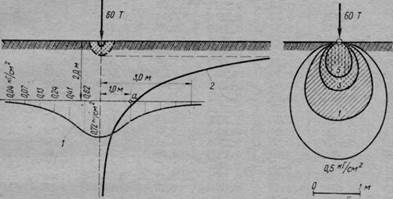
Рис. 43. К примеру определения сжимающих напряжений в грунте при действии сосредоточенной силы:
а — па глубине г=2 м (1) и по вертикальной оси 2 (2); 6 — линии одинаковых
давлений
2(г; = 0). Следует отметить, что в точке приложения сосредоточенной силы, естественно, получаются бесконечно большие давления. На практике же их не будет, так как нельзя сосредоточить большой груз в одной точке, при малой же площади передачи нагрузки напряжения в месте приложения нагрузки превзойдут предел прочности грунта, поэтому некоторую область (заштрихованную на рис. 43, а) у точки приложения сосредоточенной силы необходимо исключить из рассмотрения.
По найденным для ряда точек (площадок) напряжениям о2 на рис. 43', б построены линии одинаковых сжимающих напряжений — «.изобары», наглядно иллюстрирующие всю «луковицу» давлений.
Сосредоточенная сила (2 приложена на поверхности параллельно ограничивающей полупространство плоскости. В этом случае вертикальное сжимающее напряжение о2 будет определяться выражением
0г=тт-ж- (ШЛ)
где у — координата, параллельная силе С};
Я — расстояние до любой точки (Р2 = х + у2 + г2),
Таблица 8
Значение коэффициента К для вычисления сжимающих напряжений от действия сосредоточенной силы в зависимости от отношения г/г
| г/г | к | г/г | к | г/г | к | г/г | АГ | ||||||
| ,4775 | 0,50 | ,00 | 1,50 | ||||||||||
| ,4773 | 0,51 | ,01 | 1,51 | ||||||||||
| ,4770 | 0,52 | ,02 | 1,52 | ||||||||||
| ,4764 | 0,53 | ,03 | 1,53 | ||||||||||
| ,4756 | 0,54 | ,04 | 1,54 | ||||||||||
| ,4745 | 0,55 | ,05 | 1,55 | ||||||||||
| ,4732 | 0,56 | ,06 | 1,56 | ||||||||||
| ,4717 | 0,57 | ,07 | 1,57 | ||||||||||
| ,4699 | 0,58 | ,08 | 1,58 | ||||||||||
| ,4679 | 0,59 | ,09 | 1,59 | ||||||||||
| ,4657 | 0,60 | ,10 | 1,60 | ||||||||||
| ,4633 | 0,61 | ,11 | 1,61 | ||||||||||
| 4607 ' | 0,62 | ,12 | 1,62 | ||||||||||
| ,4579 | 0,63 | ,13 | 1,63 | ||||||||||
| ,4548 | 0,64 | 1,64 | |||||||||||
| ,4516 | 0,65 | ,15 | 1,65 | ||||||||||
| ,4482 | 0,66 | ,16 | 1,66 | ||||||||||
| 0,67 | ,17 | 1,67 | |||||||||||
| 0,68 | ,18 | 1,68 | |||||||||||
| 0,69 | ,19 | 1,69 | |||||||||||
| 0,70 | ,20 | 1,70 | |||||||||||
| 0,71 | ,21 | 1,72 | |||||||||||
| 0,72 | ,22 | 1,74 | |||||||||||
| 0,73 | ,23 | 1,76 | |||||||||||
| 0,74 | ,24 | 1,78 | |||||||||||
| 0,75 | ,25 | 1,80 | |||||||||||
| 0,76 | ,26 | 1,82 | |||||||||||
| 0,77 | ,27 | 1,84 | |||||||||||
| о | 0,78 | ,28 | 1,86 | ||||||||||
| 0,79 | ,29 | 1,88 | |||||||||||
| 0,80 | ,30 | ,0402 | 1,90 | ||||||||||
| ,31 | 0,81 | ,31 | 1,92 | ||||||||||
| 0,82 | ,32 | 1,94 | |||||||||||
| 0,83 | ,33 | 1,96 | |||||||||||
| 0,84 | ,34 | 1,98 | |||||||||||
| 0,85 | ,35 | 2,00 | |||||||||||
| 0,86 | ,36 | 2,10 | |||||||||||
| 0,87 | ,37 | 2,20 | |||||||||||
| 0,88 | ,38 | 2,30 | |||||||||||
| 0,89 | . 1 | ,39 | 2,40 | ||||||||||
| 0,90 | ,40 | ,0317 | 2,50 | ||||||||||
| 0,91 | ,41 | 2,60 | |||||||||||
| 0,92 | ,42 | ,0302 | 2,70 | ||||||||||
| ,3124 | 0,93 | ,43 | ,0295 | 2,80 | |||||||||
| ,3068 | 0,94 | ,44 | ,0288 | 2,90 | |||||||||
| ЗОН | 0,95 | ,45 | ,0282 | 3,00 | |||||||||
| ,46 | ,2955 | 0,96 | ,46 | ,0275 | 3,50 | ||||||||
| .47 | ,2899 | 0,97 | ,0910 | ,47 | ,0269 | 4,00 | |||||||
| ,2843 | 0,98 | ,0887 | ,48 | ,0263 | 4,50 | ||||||||
| 0,99 | ,0865 | ,49 | ,0257 | 5,00 |
а сумма главных напряжений 6 будет определяться выражением (111.2), в котором координата г заменяется на у:
в = -^(1 + р0)А (Ш.2')
Я /с*
Зная выражения для сил (вертикальной Р и горизонтальной (2), легко определить сжимающие напряжения и сумму главных напряжений для любой наклонной силы.
Действие равномерно распределенной нагрузки. В настоящее время замкнутое строгое решение этой задачи получено лишь для прямоугольной площади загрузки, деформации которой соответствуют деформациям поверхности линейно деформируемого полупространства, т. е. для условий весьма гибкой передачи нагрузки.
Приведем результаты наиболее простого решения (А. Ляв, 1935 г.).
Сжимающее напряжение огс и сумма главных напряжений вс в любой точке, лежащей на вертикали под углом загруженного прямоугольника со сторонами / и Ь, которые мы назовем угловыми, будут равны:
р г 1Ьг /2+62+2г2 СТгс=2я^-— ■ "» +
-4- агс 31П
рггг + /252 1Ь
у г2 + г2 у&2 + г2
(Ш.5)
— (1 + р0)агс1§-
я РУ1 + а2+р2
где
а = Б \2
I
- и р
г
(4)
/2 + & _|_ гг
(Ш.6)
Пользуясь приведенными формулами, легко можно вычислить и максимальное сжимающее напряжение под центром площади загрузки аг, а также максимальное значение суммы главных напряжений вшах-
Дата добавления: 2016-06-02; просмотров: 3057;
