Черт.4.4. К примеру расчета 42

Требуется произвести расчет по раскрытию нормальных трещин

Расчет. Из черт.4.4 имеем: b =85 мм, h = 400 мм, а = 58 мм, b'_f = 725мм; h'_f = 50мм.

Определим момент образования трещин М_сrс согласно п.4.5. Для этого определяем геометрические характеристики приведенного сечения при 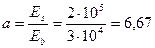и A'_s = 0;

A_red = А + aA_s = bh + (b'_f - b)h'_f + aA_s = 85·400 + (725 - 85)50 + 6,67·760 = 34000 + 32000 + 5069 = 71069 мм²;

у_t = S_red / A_red = [34000·400/2 + 32000(400-50/2) + 5069·58]/71069 = 268,7 мм;

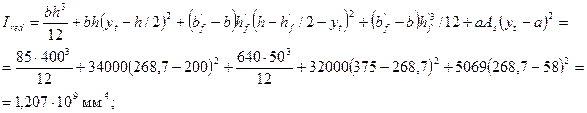
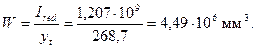
Учтем неупругие деформации растянутого бетона путем умножения W на коэффициент γ, равный согласно табл.4.1 1,30, т.е. W = 4,49·10⁶·1,3 = 5,84·10⁶ мм³. Тогда М_сrс = R_bt,ser W = 1,55·5,84·10⁶ = 9,052·10⁶ Нмм = 9,05 кНм < М = 69 кНм. т.е. трещины образуются и расчет по раскрытию трещин необходим.

Определим напряжение в арматуре σ_s по формуле (4.13). Рабочая высота сечения h_o = h - а = 400 - 58 = 342 мм; коэффициент приведения 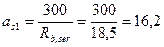. Тогда при 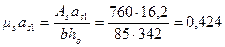и и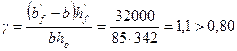з графика на черт.4.2 находим коэффициент ζ = 0,9 и плечо внутренней пары сил равно z_s = ζ·h_o = 0,9·342 = 308 мм.

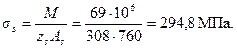
Определим расстояние между трещинами l_s по формуле (4.22).

Поскольку высота растянутого бетона, равная у = y_tk = 268,7·0,9 = 247,8 мм > h/2= 200 мм, площадь сечения растянутого бетона принимаем равной

А_bt =b·0,5h = 85·200 = 17000 мм².

Тогда

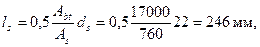
что меньше 40d_s = 880 мм и меньше 400 мм, поэтому оставляем l_s = 246 мм.

Значение ψ_s определим по формуле (4.26)

.

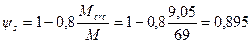Определяем по формуле (4.10) ширину продолжительного раскрытия трещин, принимая φ₁= 1,4, φ₂= 0,5 и φ₃= 1,0,

что меньше предельно допустимой ширины продолжительного раскрытия трещин, равной согласно п.4.2 a_crc,_ult = 0,3 мм.

Пример43. Дано:железобетонная плита фундамента с размерами поперечного сечения h = 300 мм, b = 1150 мм; а = 42 мм; бетон класса В15 (R_bt,ser = 1,1 МПа, R_b,ser = 11 МПа); рабочая арматура класса А400 с площадью сечения А_s = 923 мм² (6Æ14); момент в расчетном сечении от постоянных и длительных нагрузок М_l = 50 кНм, от кратковременных нагрузок M_sh = 10 кНм; фундамент эксплуатируется в неагрессивных условиях (выше верхнего уровня грунтовых вод).

Требуется произвести расчет по раскрытию нормальных трещин.

Расчет. Определим момент образования трещин М_сrс согласно пп.4.5-4.8. Поскольку 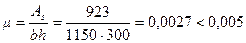, упругий момент сопротивления W определим без учета арматуры ,т.е.

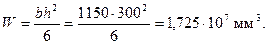
Учтем неупругие деформации растянутого бетона путем умножения W на коэффициент γ равный согласно табл.4.1 1,30, т.е. W = 1,3·1,725·10⁷ = 2,24·10⁷ мм³. Тогда M_crc = R_bt,ser W = 1,1·2,24·10⁷ = 24,67·10⁶ Нмм = 24,67 кНм < М = M_l + M_sh = 50 + 10 = 60 кНм. т.е. трещины при действии полной нагрузки образуются и расчет по раскрытию трещин необходим.

Проверим условие (4.29) с заменой напряжений σ_s соответствующими моментами

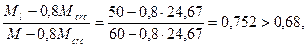
следовательно, проверяем только продолжительное раскрытие трещин. Определяем напряжение в арматуре σ_s по формуле (4.13), принимая М = М_l. Рабочая высота сечения h_o = h - а =300 - 42 = 258 мм; коэффициент приведения 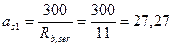. Тогда при 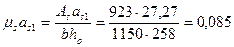и γ = 0,0 из графика на черт.4.3 находим ζ = 0,89. Плечо внутренней пары сил равно z_s = ζ·h_o = 0,89·258 = 229,6мм.

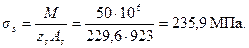
Для прямоугольного сечения высота растянутой зоны бетона с учетом неупругих деформаций равна у = 0,5hk = 0,5·300·0,9 = 135 мм > 2h = 2·42 = 84 мм и, кроме того, у = 135 мм < 0,5h = 150 мм поэтому оставляем у = 135 мм и тогда A_bt = b·у =1150·135 = 155250 мм². Расстояние между трещинами определим по формуле (4.22) 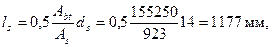, что больше 40d_s = 40·14 = 560 мм и более 400 мм, поэтому принимаем l_s = 400 мм.

Значение ψ_s определяем по формуле (4.26), принимая М = M_l = 50 кН м.

.

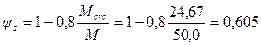Определяем по формуле (4.10) ширину продолжительного раскрытия трещин, принимая φ₁= 1,4, φ₂= 0,5 и φ₃= 1,0:

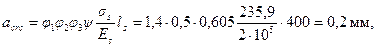
что меньше предельно допустимой ширины продолжительного раскрытия трещин, равной а_crc,_ult =0,3 мм.

Пример 44.Дано: железобетонная колонна промышленного здания, с размерами поперечного сечения h =500 мм, b = 400 мм; а = а' = 50 мм; бетон класса В15 (Е_b =24000 МПа, R_b,ser = 11 МПа, R_bt,ser =1,1 МПа); рабочая арматура класса А400 с площадью сечения A_s = А'_s = 1232 мм² (2Æ28); усилия от постоянных и длительных нагрузок: N_l = 500 кН, М_l = 150 кНм; усилия от кратковременной (ветровой) нагрузки: N_sh = 0,0; M_sh =90 кНм.

Требуется рассчитать колонну по раскрытию трещин

Расчет. Определяем момент образования трещин М_сrс согласно пп.4.5-4.8.

Поскольку 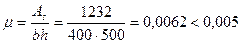, определяем значения W и е_я с учетом арматуры при коэффициенте приведения 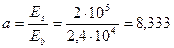. Для прямоугольного сечения с симметричной арматурой y_t = h/2 = 250 мм, а момент инерции I_red равен

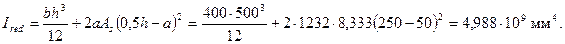
Тогда .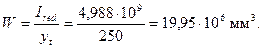

Площадь приведенного сечения равна

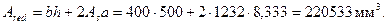
Тогда .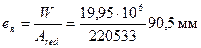

Учитываем неупругие деформации растянутого бетона путем умножения W на коэффициент γ = 1,3 (см.табл.4.1), т.е. W = 19,95·10⁶ ·1,3 = 25,94·10⁶ мм,

Определяем момент М_сrc по формуле (4.4), принимая N = N_l = 500 кН,

M_crc = R_bt,serW + Ne_я = 1,1·25,94·10⁶ + 500000·90,5 = 73,76·10⁶ Hмм = 73,76 кНм < M = M_l + M_sh = 150 + 90 = 240 кНм,

т.е. трещины при действии всех нагрузок образуются и расчет по раскрытию трещин необходим.

Определяем напряжение в растянутой арматуре при действии всех нагрузок по формуле (4.19).

h_o = h - а = 500 - 50 = 450 мм = 0,45 м.

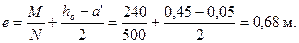
При 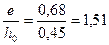и и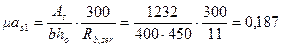з табл.4.2 находим φ_сrс = 0,54. Тогда

Аналогично определяем напряжение σ_s при действии постоянных и длительных нагрузок, т.е. принимая M = M_l =150 кНм и N = N_l =500 кН.

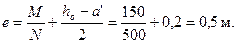
При 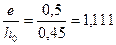и и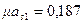з табл.4.2 находим φ_сrс = 0,32.

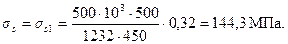
Определим также напряжение σ_s при действии момента М = М_crc = 73,76 кНм и силы N = 500 кН.

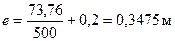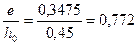; по и 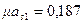находим φ_сrс = 0,08;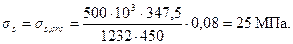

Проверим условие (4.29)

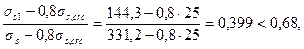
т.е. условие (4.29) не выполняется, следовательно, проверяем только непродолжительное раскрытие трещин, определяя а_сrс по формуле (4.28а). Для этого предварительно определяем a_crc,2по формуле (4.10) при φ₁= 1,0 и σ_s = 331,2 МПа.По формуле (4.25) имеем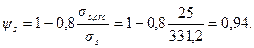

Определяем расстояние между трещинами l_s согласно п.4.12. Для этого вычислим высоту растянутой зоны бетона по формуле (4.23), принимая к = 0,90, а 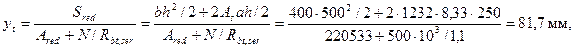y = y_tk = 81,7·0,9 = 73,5 мм < 2а = 2·50 = 100 мм.

Принимаем у = 100 мм и тогда площадь сечения растянутого бетона равна А_bt = уb = 100·400 = 40000 мм²

a .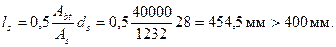

Принимаем l_s = 400 м.

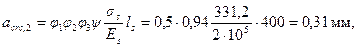
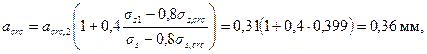
что меньше предельно допустимой ширины непродолжительного раскрытия трещин, равной 0,4 мм.