РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ПРОГИБАМ

4.17. Расчет железобетонных элементов по прогибам производят из условия

f ≤ f_ult (4.30)

где f - прогиб железобетонного элемента от действия внешней нагрузки;

f_ult- значение предельно допустимого прогиба железобетонного элемента.

Прогибы железобетонных конструкций определяют по общим правилам строительной механики в зависимости от изгибных, сдвиговых и осевых деформационных характеристик железобетонных элементов в сечениях по его длине (кривизны, углов сдвига, относительных продольных деформаций).

В тех случаях, когда прогибы железобетонных элементов, в основном, зависят от изгибных деформаций, значение прогибов определяют по кривизне элемента согласно пп.4.18 и 4.19.

4.18. Прогиб железобетонных элементов, обусловленный деформацией изгиба, определяют по формуле

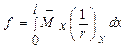, (4.31)

где 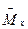- изгибающий момент в сечении х от действия единичной силы, приложенной в сечении, для которого определяется прогиб, в направлении этого прогиба;

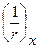- полная кривизна элемента в сечении от внешней нагрузки, при которой определяется прогиб.

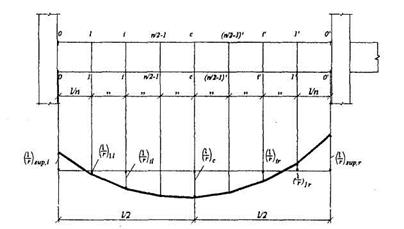
В общем случае формулу (4.31) можно реализовать путем разбиения элемента на ряд участков, определяя кривизну на границах этих участков (с учетом наличия или отсутствия трещин и знака кривизны) и перемножения эпюр моментов 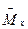и кривизны 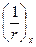по длине элемента, принимая линейное распределение кривизны в пределах каждого участка. В этом случае при определении прогиба в середине пролета формула (4.31) приобретает вид

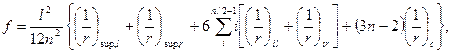(4.32)

где - кривизна элемента соответственно на левой и правой опорах;

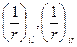- кривизна элемента в симметрично расположенных сечениях i и i' (при i = i') соответственно слева и справа от оси симметрии (середины пролета, черт.4.5);

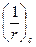- кривизна элемента в середине пролета;

п - четное число равных участков, на которое разделяют пролет, принимаемое не менее 6;

l - пролет элемента.

В формулах (4.31) и (4.32) кривизны - определяют по указаниям пп.4.21 - 4.27. При этом знак кривизны принимают в соответствии с эпюрой кривизны.